Important Formulae: Permutations & Combinations | CSAT Preparation - UPSC PDF Download
Permutation & Combination
When two tasks are performed in succession, i.e., they are connected by an 'AND', to find the total number of ways of performing the two tasks, you have to MULTIPLY the individual number of ways. When only one of the two tasks is performed, i.e. the tasks are connected by an 'OR', to find the total number of ways of performing the two tasks you have to ADD the individual number of ways.
Example: In a shop there are ‘d’ doors and ‘w’ windows.
Case 1: If a thief wants to enter via a door or window, he can do it in – (d+w) ways.
Case2: If a thief enters via a door and leaves via a window, he can do it in – (d x w) ways.
Linear arrangement of ‘r’ out of 'n' distinct items (nPr): The first item in the line can be selected in 'n' ways AND the second in (n - 1) ways AND the third in (n - 2) ways AND so on. So, the total number of ways of arranging 'r' items out of 'n' is
(n)(n - 1)(n - 2)...(n - r + 1) = 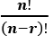
Circular arrangement of 'n' distinct items: Fix the first item and then arrange all the other items linearly with respect to the first item. This can be done in (n - 1)! Ways.
EduRev's Tip: In a necklace, it can be done in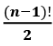 ways.
ways.
Selection of r items out of 'n' distinct items (nCr): Arrange of r items out of n = Select r items out of n and then arrange those r items on r linear positions.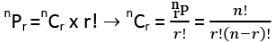
Derangement: If 'n' things are arranged in a row, the number of ways in which they can, be deranged so that none of them occupies its original place is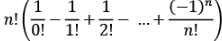
EduRev's Tip: Number of ways of arranging 'n' items out of which `p' are alike, 'q' are alike, 'r' are alike in a line is given by = 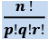
Partitioning
|
205 videos|264 docs|136 tests
|
FAQs on Important Formulae: Permutations & Combinations - CSAT Preparation - UPSC
| 1. What is the formula for permutations? |  |
| 2. What is the formula for combinations? |  |
| 3. How do permutations and combinations differ? |  |
| 4. When should I use permutations? |  |
| 5. When should I use combinations? |  |

















