Sample Question Paper- 3 | Mathematics (Maths) Class 8 PDF Download
Class - VIII
Mathematics
Time - 3 hrs
M.M. - 80 Marks
General Instructions :
1. All questions are compulsory.
2. The question paper consist of 30 questions divided into four sections A, B, C and D. Section A comprises of 6 questions of 1 mark each, Section B comprises of 6 questions of 2 marks each, Section C comprises of 10 questions of 3 marks each and Section D comprises of 8 questions of 4 marks each.
3. There is no overall choice. 4. Use of calculator is not allowed.
Section ‘A’
Q.1. Suppose that the division x ÷ 5 leaves a remainder 4 and the division x ÷ 2 leaves a remainder 1. Find the ones digit of x.
Ans. Since, x ÷ 5 leaves a remainder 4, so ones digit of x can be 4 or 9. Also, since x ÷ 2 leaves a remainder 1, so ones digit must be 9 only.
Q.2. If the sum of the digits of a number is divisible by three, then the number is divisible by which number ?
Ans. If the sum of the digits of a number is divisible by three, then the number will be divisible by 3.
Q.3. Classify the following polynomials as monomials, binomials, trinomials,
– z + 5, x + y + z, y + z + 100, ab – ac, 17
Ans.
(i) 17 is monomial
(ii) – z + 5 and ab – ac, y + z + 100 are binomials.
(iii) x + y + z is trinomial.
Q.4. What is the usual form for 2.3 × 10–10 ?
Ans. 2.3 × 10–10 = 23 × 10–1 × 10–10
= 23 × 10–11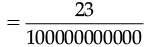
= 0.0000000023
Q.5. How many vertices are there of a sphere ?
Ans. There are 0 vertices of a sphere.
Q.6. The sides of a triangle are 3x + 1, – x + 2 and 4x + 6, then find its perimeter.
Ans.
Let
AB = 3x + 1
BC = – x + 2
AC = 4x + 6
Since, perimeter of ∆ABC = AB + BC + AC
= 3x + 1 + (– x + 2) + 4x + 6
= 3x + 1 – x + 2 + 4x + 6
= 6x + 9
SECTION ‘B’ (2 marks each)
Q.7. Simplify :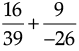
Ans.
We have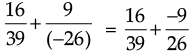
Now, the LCM of 39 and 26 is 78.
∴ Rewriting 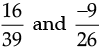 in such a manner they have the same denominator 78.
in such a manner they have the same denominator 78.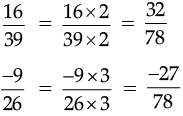
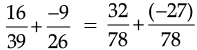

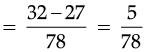
Q.8. Represent the number 7/4 on the number line.
Ans. To represent 7/4 , we make 7 markings each of a distance equal to 1/4 on the right of 0. The 7th point represent the rational number 7/4 as shown in the figure.
The point A is 7/4.
Q.9. Factorise the following :
(a) 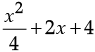
(b) 16x2 + 40x + 25
Ans. (a)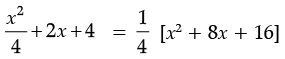
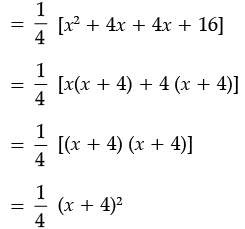
(b) 16x2 + 40x + 25 = 16x2 + (20 + 20)x + 25
= 16x2 + 20x + 20x + 25
= 4x (4x + 5) + 5(4x + 5)
= (4x + 5) (4x + 5)
= (4x + 5)2
Q.10. Evaluate :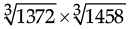
Ans.
Since,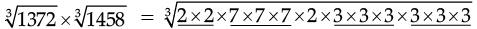
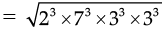
= 2 × 7 × 3 × 3
= 126
Q.11. Factorise the following :
(a) 18 + 11x + x2
(b) y2 – 2y – 15
Ans. (a) 18 + 11x + x2 = x2 + 11x + 18
= x2 + (9 + 2) x + 18
= x2 + 9x + 2x + 18
= x (x + 9) + 2 (x + 9)
= (x + 9) (x + 2)
(b) y2 – 2y – 15 = y2 – (5 – 3) y – 15
= y2 – 5y + 3y – 15
= y(y – 5) + 3(y – 5)
= (y – 5) (y + 3)
Q.12. Using a suitable identity to get the product 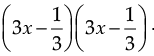
Ans. Using the identity (a – b)2 = a2 – 2ab + b2,
We have, 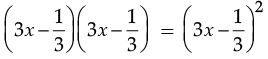
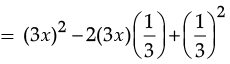
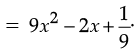
SECTION ‘C’
Q.13. (a) Find the area of rectangular park which is 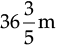 long and
long and 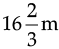 broad.
broad.
(b) Write the name of property for any rational numbers 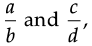 we have
we have 
Ans. (a) Since length of rectangular park 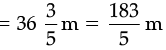
and breadth of rectangular park = 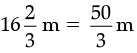
Then area of park = l × b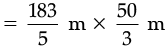
= 61 × 10 m2 = 610 m2
(b) 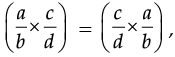 it is commutative law of property.
it is commutative law of property.
Q.14. Observe the following table, where x and y are in inverse variation :
Find the unknown quantities.
Ans. Let x1 = p1, x2 = 200, x3 = 300
and y1 = 60, y2 = 30, y3 = p2
Since, x and y are in inverse variation.
(a) ∴ x1y1 = x2y2
⇒ p1 × 60 = 200 × 30
∴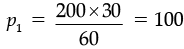
(b) Also, x2y2 = x3y3
⇒ 200 × 30 = 300 × p2
∴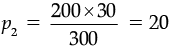
Q.15. Construct the following quadrilaterals
Quadrilateral ABCD
AB = 4.5 cm
BC = 5.5 cm
CD = 4 cm
AD = 6 cm
AC = 7 cm
Ans. Steps of construction :
(1) First, we draw ABC using SSS construction condition.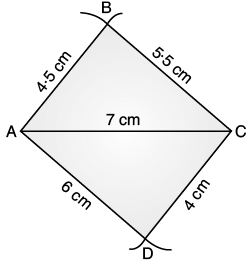 (2) Now, we have to locate the fourth point D. This ‘D’ would be on the side opposite to B with reference to AC.
(2) Now, we have to locate the fourth point D. This ‘D’ would be on the side opposite to B with reference to AC.
(3) D is 6 cm away from A. So, draw an arc of radius 6cm. D is 4 cm away from A. So, draw an arc of radius 4 cm.
(4) D should be lie on both the arcs drawn. So, its the point of intersection of the two arcs. ABCD is the required quadrilateral.
Q.16. By what number should (–8)–3 be multiplied so that the product may be equal to (–6)–3 ?
Ans. Let the number be x
(–8)–3 × x = (–6)–3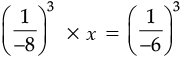
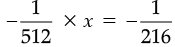
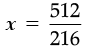
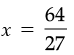
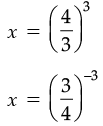
Q.17. If 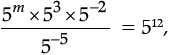 find m.
find m.
Ans.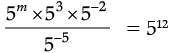
5m × 53 × 5–2 × 55 = 512
5m × 53 – 2 + 5 = 512
5m × 56 = 512
5m + 6 = 512
m + 6 = 12
m = 12 – 6
m = 6
Q.18. (a) Construct a rectangle ABCD in which side BC = 5 cm and diagonal BD = 6.2 cm.
(b) Can you draw a rhombus ZEAL, where ZE = 3.5 cm, diagonal EL = 5 cm ? Why ?
Ans. (a) Steps of Construction :
(i) Draw B C = 5 cm.
(ii) Draw CN ⊥ BC.
(iii) With B as a centre and radius 6.2 cm, draw an arc, cutting CN at D.
(iv) Join BD.
(v) With D as centre and radius 5 cm, draw an arc.
(vi) With B as centre and radius equal to CD draw another arc, cutting the previous arc at A. (vii) Join AB and AD, then ABCD is a required rectangle.
(vii) Join AB and AD, then ABCD is a required rectangle.
(b) Yes, we can draw a rhombus ZEAL because all the four sides of a rhombus are equal in length.
Q.19. Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.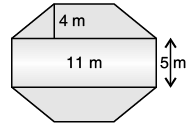
Ans. Each side of octagon surface = 5 m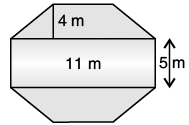
Area of octagon = 2(Area of trapezium) + Area of rectangle
= 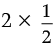 × h × (sum of parallel side) + l × b
× h × (sum of parallel side) + l × b
= 4 × (5 + 11) + 11 × 5
= 64 + 55
= 119 m2
∴ Area of octagon surface = 119 cm2.
Q.20. The parallel sides of a trapezium are 40 cm and 20 cm. If its non-parallel sides are equal, each being 26 cm, find the area of the trapezium.
Ans. Let ABCD be the trapezium such that AB = 40 cm and CD = 20 cm and AD = BC = 26 cm.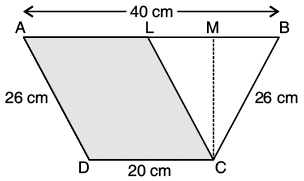
Now, draw CL || AD
Then, ALCD is a parallelogram
So, AL = CD = 20 cm and CL = AD = 26cm.
In ∆CLB, we have
CL = CB = 26 cm
Therefore, ∆ CLB is an isosceles triangle.
Draw altitude CM of ∆CLB.
Since, ∆ CLB is an isosceles triangle.
So, C M is also the median.
Then, L M = MB = 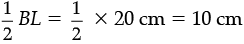
[as B L = AB – AL = (40 – 20) cm = 20 cm].
Applying Pythagoras theorem in ∆CLM,
we have,
CL2 = CM2 + LW2
262 = CM2 + 102
CM2 = 262 – 102
= (26 – 10) (26 + 10)
= 16 × 36 = 576
CM = 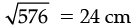
Hence, the area of the trapezium = 1/2 ×(sum of parallel sides) × Height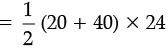
= 30 × 24 = 720 cm2
21. Factorise the following :
(a) a3 – 4a2 + 12 – 3a
(b) 4x2 – 20x + 25
Ans. (a) a3 – 4a2 + 12 – 3a= a2 (a – 4) – 3a + 12
= a2 (a – 4) – 3 (a – 4)
= (a – 4) (a2 – 3)
(b) 4x2 – 20x + 25 =(2x)2 – 2 × 2x × 5 + (5)2
= (2x – 5)2
[Since, a2 – 2ab + b2 = (a – b)2]
= (2x – 5) (2x – 5)
22. A table marked at Rs. 15,000 is available for Rs. 14,400. Find the discount given and the discount percentage ?
Ans. The marked price of table = Rs. 15,000
The selling price of tale = Rs. 14,400
According to condition,
Discount value = Marked price – Selling price
= Rs. 15, 000 – Rs. 14,400
Discount value = Rs. 600
Let us suppose that the discount % of table = x %
Discount value = Discount % of marked price
Rs. 600 = x % of Rs. 15,000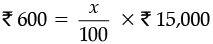
The discount value of table = Rs. 600
& The discount percent of table = 4%
SECTION ‘D’
Q.23. Let a, b, c, be the three rational numbers where a = 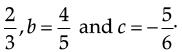
Verify :
(a) a + (b+c) = (a + b) + c (Associative property of addition).
(b) a × (b × c) = (a × b) × c (Associative property of multiplication).
Ans. (a) L.H.S = a + (b + c)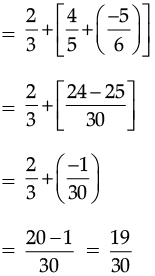
R.H.S. of (i) = (a + b) + c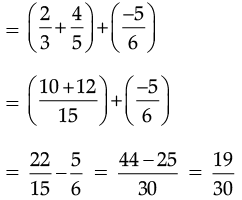
So, 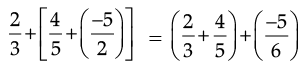 Hence Verified
Hence Verified
(b) L.H.S = a × (b × c)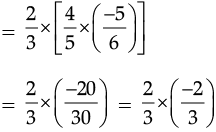
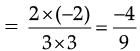
R.H.S. = (a × b) × c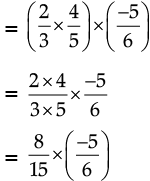
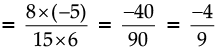
So, 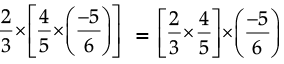 Hence Verified
Hence Verified
Q.24. Find the three rational numbers between 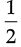 and – 2.
and – 2.
Ans. A rational number between 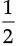 and – 2
and – 2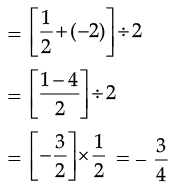
A rational number between 
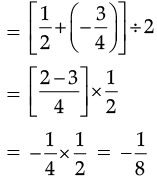
A rational number between 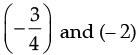
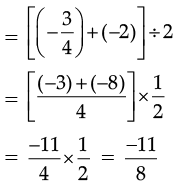
Thus, the three rational numbers are 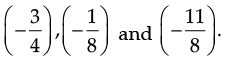
Q.25. The product of two rational numbers is 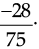 If one of the numbers is
If one of the numbers is 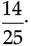 Find the other.
Find the other.
Ans. ∵ Product of two numbers = 
Any one of the rational number = 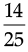
∴ The other number = 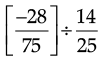
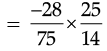
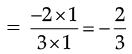
Thus, the required rational number is 
Q.26. Diameter of cylinder A is 7 cm and the height is 14 cm. Diameter of cylinder B is 14 cm and height is 7 cm. Without doing any calculations can you suggest whose volume is greater ? Verify it by finding the volume of both the cylinders. Check whether the cylinder with greater volume also has greater surface area.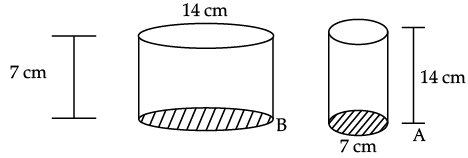 Ans. Volume of cylinder B is greater because it contains more thickness in comparison to A.
Ans. Volume of cylinder B is greater because it contains more thickness in comparison to A.
For cylinder B, r = 7 cm, h = 7 cm
Volume of cylinder B = πr2h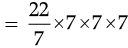
= 1078 cm3.
Surface area of cylinder B = 2πrh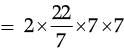
For cylinder A, = 308 cm2
radius of cylinder A = 3.5 cm, h = 14 cm
Volume A = πr2h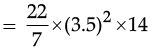
= 539 cm2
Surface area of cylinder A = 2πrh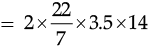
= 308 cm2
Volume of cylinder B > volume of cylinder A.
Surface area of both cylinders are same.
Q.27. Hasan buys two kinds of cloth materials for school uniforms, shirt material that costs him Rs. 50 per metre and trouser material that costs him Rs. 90 per metre. For every 3 metres of the shirt material he buys 2 metres of the trouser material. He sells the materials at 12% and 10%, respectively. His total sale is Rs. 36,600. How much trouser material did he buy ?
Ans. Let shirt material be 3x and trouser material be 2x metres.
The cost of shirt material = 50 × 3x = 150x
The selling price at 12% profit = 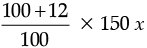
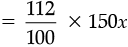
= 168 x
The cost of trouser material = 90 × 2x = 180x
The selling price at 10% profit = 
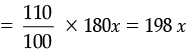
According to question, 168x + 198x = 36,600
or, 366x = 36,600
or, 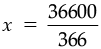
or, x = 100
∴ Trouser material = 2 × 100 = 200 m
Hence, Hasan bought 200 m trouser material.
Q.28. (a) Find the value of the expression (81x2 + 16y2 – 72xy), when x =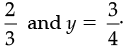
Ans. (a) 81x2 + 16y2 – 72xy= (9x)2 + (4y)2 – 2 × 9x × 4y
= (9x – 4y)2 [∵ a2 + b2 – 2ab = (a – b)2]
Now, putting x = 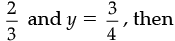
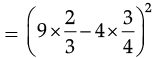
= (6 – 3)2 = 32 = 9
(b) Putting a = 2 and b = 5, then
L.H.S = (a + b)2
= (2 + 5)2 = 72 = 49
and R.H.S = a2 + b2 + 2ab
= 22 + 52 + 2 × 2 × 5
= 4 + 25 + 20 = 49
Hence, L.H.S = R.H.S = 49
Q.29. A shopkeeper bought two TV sets at Rs. 10,000 each. He sold one at a profit 10% and the other at a loss of 10%. Find whether he made an overall profit or loss.
Ans. In first case, when shopkeeper found a profit.
Cost Price (C.P.) = Rs. 10,000
Profit% = 10%
Selling Price (S.P.) = ?
We know that,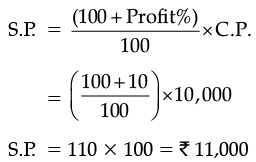
S.P. = 110 × 100 = Rs. 11,000
Selling price (S.P.) of first case = Rs. 11,000
In second case,
When shopkeeper found a loss,
C.P. = Rs. 10,000
Loss% = 10%
S.P. = ?
We know that,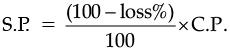
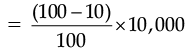
= 90 × 100
S.P. = Rs. 9,000
S.P. of second case = Rs. 9,000
According to whole transaction,
Total C.P. of both cases = 10,000 × 2 = Rs. 20,000
Total S.P. of both cases = (11,000 + 9,000)
= Rs. 20,000
Hence, these is no profit or no loss.
Q.30. (a) Add : p (p – q), q (q – r) and r (r – p)
(b) Add : 2x (z – x – y) and 2y (z – y – x)
(c) Subtract : 3l (l – 4m + 5n) from 4l ( 10n – 3m + 2l)
(d) Subtract : 3a (a + b + c) – 2b (a – b + c) from 4c (– a + b + c)
Ans. (a) First expression = p (p – q) = p2 – pq
Second expression = q (q – r) = q2 – qr
Third expression = r (r – p) = r2 – rp
Now, adding three expression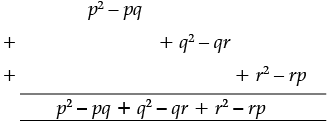
Therefore, p2 + q2 + r2 – (pq + qr + rp)
(b) First expression = 2x (z – x – y) = 2xz – 2x2 – 2xy
Second expression= 2y (z – y – x) = 2yz – 2y2 – 2xy
Now, adding the two expressions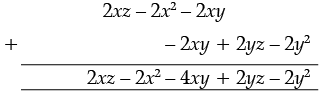
Therefore, – 2x2 – 2y2 – 4xy + 2xz + 2yz
(c) We have, 3l (l – 4m + 5n)
= 3l2 – 12lm + 15ln
and l (10n – 3m + 2l) = 40ln – 12lm + 8l2
Now, 40ln – 12lm + 8l2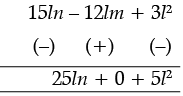
Therefore, 5l2 + 25ln
(d) We have, 3a (a + b + c) – 2b (a – b + c)
= 3a2 + 3ab + 3ac – (2ab – 2b2 + 2bc)
= 3a2 + 3ab + 3ac – 2ab + 2b2 – 2bc)
= 3a2 + 2b2 + ab + 3ac – 2bc
and 4c (– a + b + c) = – 4ac + 4bc + 4c2
Now, – 4ac + 4bc + 4c2 – (3a2 + 2b2 + ab + 3ac – 2bc)
= – 4ac + 4bc + 4c2 – 3a2 – 2b2 – ab – 3ac + 2bc)
= – 3a2 – 2b2 + 4c2 – ab – 7ac + 6bc
Therefore, – 3a2 – 2b2 + 4c2 – ab + 6bc – 7ac
|
81 videos|411 docs|31 tests
|
FAQs on Sample Question Paper- 3 - Mathematics (Maths) Class 8
| 1. What is the format of the Class 8 exam for the academic year 2020-21? |  |
| 2. How can I prepare for the Class 8 exam effectively? |  |
| 3. What resources can I use to study for the Class 8 exam? |  |
| 4. How can I manage my time during the Class 8 exam? |  |
| 5. How can I stay calm and focused during the Class 8 exam? |  |