Mathematics: CBSE Sample Question Paper (2020-21)- 2 | Mathematics (Maths) Class 12 - JEE PDF Download
| Table of contents |

|
| PART - ASection - I |

|
| Section - II |

|
| PART - B |

|
| Section-III |

|
| Section - IV |

|
| Section - V |

|
Class - XII
Math
TIME: 3 Hrs.
M.M: 80
General Instructions:
1. This question paper contains two parts A and B. Each part is compulsory. Part A carries 24 marks and Part B carries 56 marks.
2. Part-A has Objective Type Questions and Part-B has Descriptive Type Questions.
3. Both Part A and Part B have choices.
Part – A :
1. It consists of two sections- I and II.
2. Section I comprises of 16 very short answer type questions.
3. Section II contains 2 case studies. Each case study comprises of 5 case-based MCQs. An examinee is to attempt any 4 out of 5 MCQs.
Part – B :
1. It consists of three sections-III, IV and V.
2. Section III comprises of 10 questions of 2 marks each.
3. Section IV comprises of 7 questions of 3 marks each.
4. Section V comprises of 3 questions of 5 marks each.
5. Internal choice is provided in 3 questions of Section –III, 2 questions of Section -IV and
3 questions of Section-V. You have to attempt only one of the alternatives in all such questions.
PART - A
Section - I
Question numbers 1 to 16 are very short answer type questions.
Q.1. If A = [aij]mxn is a square matrix, then compare m and n.
Ans. It is known that a given matrix is said to be a square matrix if the number of rows is equal to the number of columns. Therefore,
If A = [aij]mxn is a square matrix, if m = n.
Q.2. 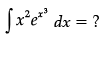
OR
Find the value of 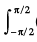 (x3 + x cos x + tan5 x+ 1) dx?
(x3 + x cos x + tan5 x+ 1) dx?
Ans. Given 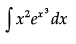
Put x3 = y
⇒ 3x2dx = dy
Then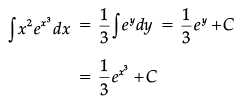
Let,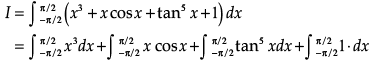
It is known that if f(x) is an even function,
then 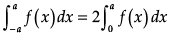 and if f(x) is an odd function, then
and if f(x) is an odd function, then
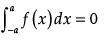
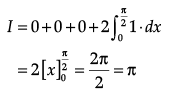
Q.3. If A = [2 –3 4], B =  , X = [1 2 3] and Y =
, X = [1 2 3] and Y = 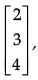 then find AB + XY.
then find AB + XY.
Ans. Given, A = [2 -3 4],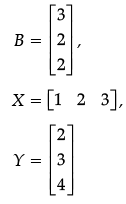
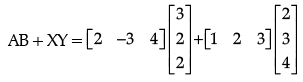
= [6 – 6 + 8] + [2 + 6 + 12]
= [8] + [20] = [28]
OR
If A = 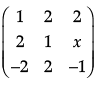 is a matrix satisfying AA’ = 9I, find x.
is a matrix satisfying AA’ = 9I, find x.
Ans.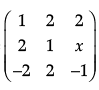
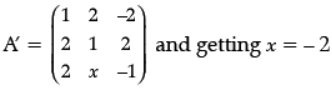
Detailed Solution :
Given: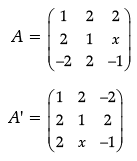
Since, AA' = 9I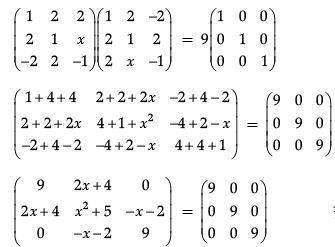
Now, x2 + 5 = 9
x2 = 9 – 5
x2 = 4
x = √4
x = ± 2
Also, 2x + 4 = 0
2x = – 4
x = − 4/2
So, x = – 2
Q.4. Evaluate: 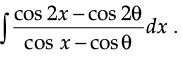
Ans.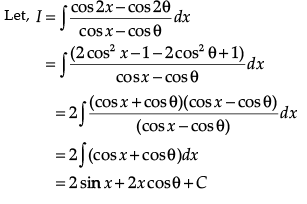
= 2(sin x + x cos q) + C
OR
Find: 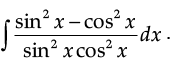
Ans.
Let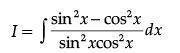
= ∫ (sec2 x − cosec2x) dx
= tan x + cot x + C
Q.5. Find where the function f(x) = e|x| is continuous and differentiable ?
Ans. Given that,
f(x) = e|x|
The functions ex and |x| are continuous functions for all real value of x.
Since ex is differentiable everywhere but |x| is non-differentiable at x = 0.
Thus, the given functions f(x) = e|x| is continuous everywhere but not differentiable at x = 0.
Q.6.The curve y = x1/5 has at (0, 0) is parallel to which axis?
Ans. Given that, y =x1/5 On differentiating with respect to x, we get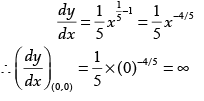
So, the curve y =x1/5 has a vertical tangent at (0, 0), which is parallel to y-axis.
Q.7. If the directions cosines of a line are k, k, k, then find the value of k.
Ans. Since, direction cosines of a line are k, k and k.
∴ l = k, m = k and n = k
We know that, l2 + m2 + n2 = 1
⇒ k2 +k2+k2 = 1
⇒ k2 = 1/3
∴ k = ± 1/√3
Q.8. A number is chosen randomly from numbers 1 to 60. What is the probability that the chosen number is a multiple of 2 or 5?
Ans.
Let us suppose A : Number is multiple of 2.
Let us suppose B : Number is multiple of 5.
Then n(A) = 30
n(B) = 12
n(A ∩ B) = 6
⇒ P(A or B) = P(A) + P(B) – P(A and B)
⇒ P(A or B) = 30/60 + 12/60 -6/60 = 36/60
⇒ P(A or B) = 3/5
Q.9. A card is picked at random from a pack of 52 playing cards. Given that the picked card is a queen, then what is the probability of this card to be a card of spade ?
Ans.
P(A/B) = 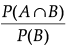
where, A : The card is spade
B : The picked card is queen
⇒ 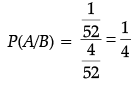
OR
A black and a red die are rolled together. Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.
Ans.
A : Getting a sum of 8,
B : Red die resulted in no. < 4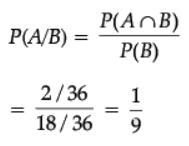
Q.10. A die is thrown once. Let A be the event that the number obtained is greater than 3. Let B be the event that the number obtained is less than 5. Then find P(A ∪ B).
Ans.
A = {4, 5, 6}
and B = {1, 2, 3, 4}
Here A ∩ B = {4}
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 3/6 + 4/6 + 1/6 = 1
Q.11. If 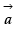 is a non-zero vector, then what is the value of
is a non-zero vector, then what is the value of 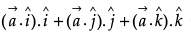 ?
?
Ans.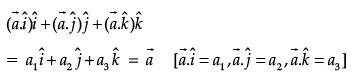
OR
Find the projection of the vector  on the vector
on the vector 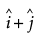
Ans. Let,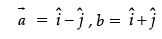
The projection of the vector 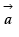 on the vector
on the vector 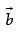
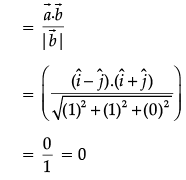
Q.12. If the function f(x) = 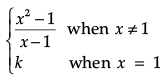 when when is given to be continuous at x = 1, then what is the value of k ?
when when is given to be continuous at x = 1, then what is the value of k ?
Ans.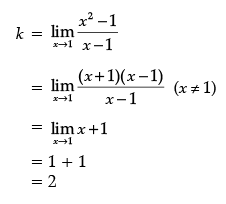
Q.13. Explain 'Identity relation'.
Ans. In Identity relation; every element of a set always related to itself.
Q.14. 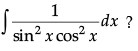
Ans.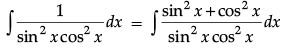
= ∫(sec2 x + cosec2x)dx
= tan x – cot x + C
Q.15. Evaluate: 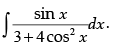
Ans. 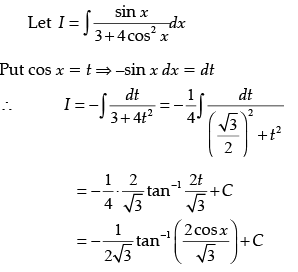
OR
Evaluate: 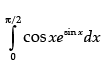
Ans.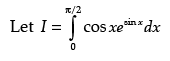
P sin x = t ⇒ cos x dx = dt
As x → 0, then t → 0
and x → π/2, then t → 1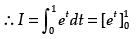
= e1 - e0 = e - 1
Q.16. If A = {1, 2, 3}, B = {4, 5, 6, 7} and f = {(1, 4), (2, 5), (3, 6)} is a function from A to B. State whether f is one-one or not.
Ans. Given, A = {1, 2, 3}, B = {4, 5, 6, 7} and f : A → B is defined as f = {(1, 4), (2, 5), (3, 6)} i.e. f(1) = 4, f(2) = 5 and f(3) = 6.
It can be seen that the images of distinct elements of A under f are distinct. So, f is one-one.
Section - II
Both the case study based questions are compulsory. Attempt any 4 sub parts from each question 17 and 18. Each question carries 1 mark.
Q.17. As we know, our planet earth revolves around the sun in an elliptical orbit. So, let suppose there is an rectangle that can be inscribed in an ellipse 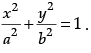

Based on the above information answer the following questions:
(i) The area of rectangle ABCD is:
(a)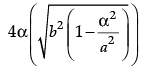
(b) 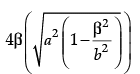
(c) 4a(b – a)
(d) 4b(a – b)
Ans. a
(ii) The value of 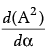 da is:
da is:
(a)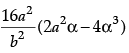
(b)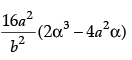
(c) 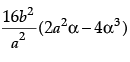
(d)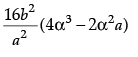
Ans. c
(iii) The value of a is :
(a) 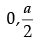
(b) 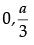
(c) 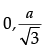
(d) 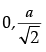
Ans. d
(iv) For what value of a, A is maximum ?
(a) 0
(b) 2a
(c) 3a
(d) 2a
Ans. d
(v) The greatest area of rectangle that can be inscribed in that ellipse is :
(a) 2αβ
(b) 2ab
(c) 4αβ
(d) 4ab
Ans. b
Q.18. A group of people start playing cards. And as we know a well shuffled pack of cards contains a total of 52 cards. Then 2 cards are drawn simultaneously (or successively without replacement).
Based on the above information answer the following:
(i) If x = no. of kings = 0, 1, 2. Then P(x = 0) = ?
(a) 188/221
(b) 198/223
(c) 197/290
(d) 187/221
Ans. a
(ii) If x = no. of kings = 0, 1, 2. Then P(x = 1) = ?
(a) 32/229
(b) 32/227
(c) 32/221
(d) 32/219
Ans. c
(iii) If x = no. of kings = 0, 1, 2. Then P(x = 2) = ?
(a) 2/219
(b) 1/221
(c) 3/209
(d) 1/209
Ans. b
(iv) Find the mean of the number of kings ?
(a) 2/13
(b) 1/13
(c) 1/17
(d) 2/17
Ans. a
(v) Find the variance of the number of kings ?
(a) 400/2873
(b) 400/2877
(c) 400/2879
(d) 400/2871
Ans. a
PART - B
Section-III
Question numbers 19 to 28 carry 2 marks each.
Q.19. If A = 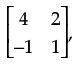 , show that (A – 2I) (A – 3I) = 0.
, show that (A – 2I) (A – 3I) = 0.
Ans. 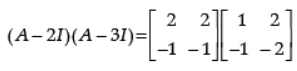
Detailed Solution :
Given: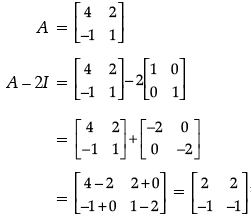
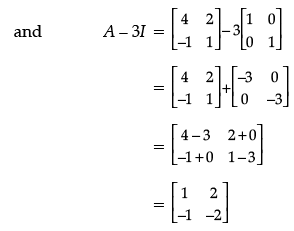
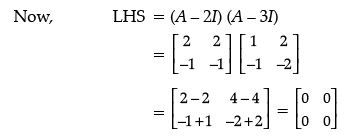
= 0 = RHS
OR
If A =  , then find (A2 – 5A).
, then find (A2 – 5A).
Ans.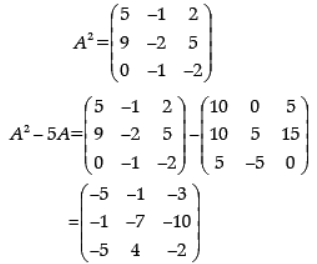
Detailed Solution:
Given: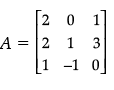
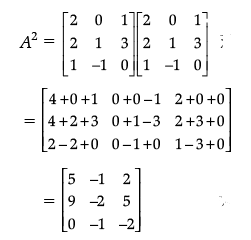
Now,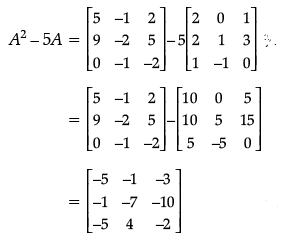
Q.20. If P(not A) = 0.7, P(B) = 0.7 and P(B/A) = 0.5, then find P(A/B).
Ans. P(notA) = 0.7 ⇒ 1 - P(A) = 0.7 ⇒ P(A) = 0.3
P(A ∩ B) = P(A) × P(B| A) = 0.3 x 0.5 = 0.15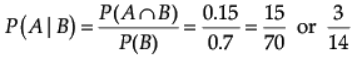
Q.21. Check if the relation R on the set A = {1, 2, 3, 4, 5, 6} defined as R = {(x, y) : y is divisible by x} is (i) symmetric (ii) transitive.
Ans.
A = {1, 2, 3, 4, 5, 6}
R = {(x, y) : y is divisible by x}
(i) Symmetric
Let (x, y) ∈ R
y is divisible by x
∴ x is not necessarily divisible by y
(y, x) ∉ R
e.g., (1, 2) ∈ R
2 is divisible by 1
but 1 is not divisible by 2
(2, 1) ∈ R
Hence, Given Relation is not symmetric 1
(ii) Transitive Let (x, y) ∈ R
y is divisible by x ...(i)
and (y, z) ∈ R
z is divisible by y ...(ii)
From eq. (i) and eq. (ii)
z is divisible by x
(x, z) ∈ R
e.g., (1, 2) ∈ R
2 is divisible by 1 ...(i)
(2, 4) ∈ R
4 is divisible by 2 ...(ii)
From eq. (i) and eq. (ii)
4 is divisible by 1
(1, 4) ∈ R
Hence, given Relation is transitive.
Q.22. Prove that the curves y2 = 4x and x2 + y2 – 6x + 1 = 0 touch each other at the point (1, 2).
Ans. Wave, y2 = 4x and x2 + y2 – 6x + 1 = 0
Since, both the curves touch each other at (1, 2), i.e., curves are passing through (1, 2).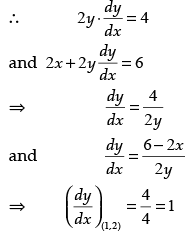
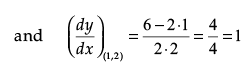
Thus, we see that slope of both the curves are equal to each other, i.e., m1 = m2 = 1 at the point (1, 2).
Hence, both the curves touch each other.
Q.23. If x = a cos θ; y = b sin q, then find d2y/dx2.
Ans. Here x = acos θ, y = bsin θ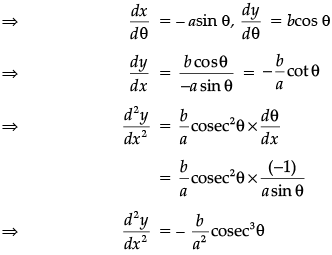
OR
Find the differential of sin2x w.r.t. ecosx.
Ans. Here, suppose u = sin2 x, v = ecos x
Then, we need to differentiate u w.r.t. to v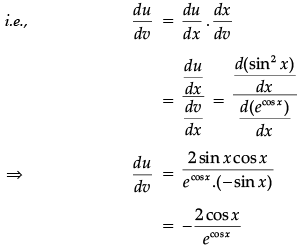
Q.24. Find the general solution of the differential equation. 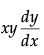 = ( x+ 2)(y +2).
= ( x+ 2)(y +2).
Ans. 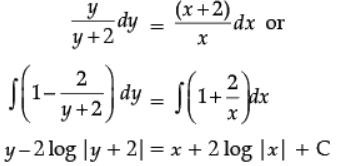
OR
Find the solution of dy/dx = 2y-x.
Ans.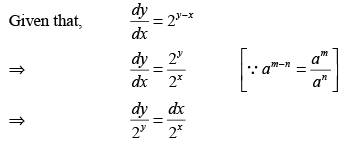
On integrating both sides, we get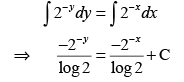
⇒ -2-y + 2-x = + Clog2
⇒ 2-x -2-y = -Clog2
⇒ 2-x - 2-y = k [where, k = +Clog2]
Q.25. Find : 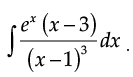
Ans.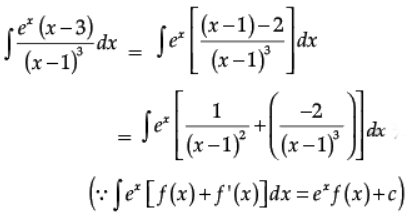
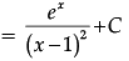
Q.26. A die, whose faces are marked 1, 2, 3 in red and 4, 5, 6 in green, is tossed. Let A be the event “number obtained is even” and B be the event “number obtained is red”. Find if A and B are independent events.
Ans. Event A : Number obtained is even B : Number obtained is red.
P(A) = 3/6 = 1/2, P(B) = 3/6 = 1/2
P (A∩B) = P (getting an even red number) = 1/6
SinceP(A) · P(B) = 1/2,1/2· = 1/4 ≠ P(A ∩ B)
which is 1/6
∴ A and B are not independent events.
Q.27. Show that f : N → N, given by f(x) = 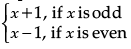 is both one-one and onto.
is both one-one and onto.
Ans. Let x1 be odd and x2 be even and suppose
f(x1) = f(x2)
or x1 + 1 = x2 – 1
or x2 – x1 = 2, which is not possible
Similarly, if x2 is odd and x1 is even, not possible to have
f(x1) = f(x2)
Let x1 and x2 be both odd
or f(x1) = f(x2) or x1 = x2
Similarly, if x1 and x2 are both even, then also
x1 = x2
∴ f is one-one.
Also, any odd number 2r + 1 in co-domain N is the image of (2r + 2) in domain N and any even number 2r in the co-domain N is the image of (2r – 1) in domain N
∴ f is onto.
Detailed Solution:
Suppose f(x1) = f(x2).
Note that if x1 is odd and x2 is even,
then we will have x1 + 1 = x2 – 1
or x1 – x2 = – 2
which is impossible.
Similarly, the possibility of x1 being even and x2 being odd can also be ruled out, using the similar argument.
Therefore, both x1 and x2 must be either odd or even.
Suppose both x1 and x2 are odd,
then f(x1) = f(x2)
or x1 + 1 = x2 + 1
or x1 = x2.
Similarly, if both x1 and x2 are even,
then also f(x1) = f(x2)
or x1 – 1 = x2 – 1
or x1 = x2.
Thus, f is on e-one.
Also, let x be an arbitrary element in N.
If x is odd, then there exists an even number x + 1 ∈
N such that f(x + 1) = x + 1 – 1 = x.
Similarly, if x is even, then there exists an odd number x – 1 ∈ N such that
f(x – 1) = x – 1 + 1 = x.
Hence, f is on e-one as well as onto.
Q.28. If the following function is differentiable at x = 2, then find the values of a and b: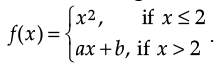
Ans. Since, f is differentiable at x = 2, therefore f is continuous at x = 2
by eqn. (i), 2a + b = 4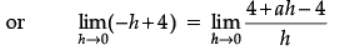
∴ 4 = a By (ii)
and b = 4 – 2a = – 4
Hence, value of a = 4 and b = – 4.
Section - IV
Question Numbers 29 to 35 carry 3 marks each.
Q.29. Let 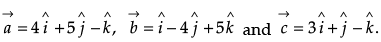 Find a vector
Find a vector 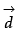 which is perpendicular to both
which is perpendicular to both 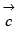 and
and 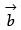 and satisfying
and satisfying 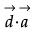 · = 21.
· = 21.
Ans.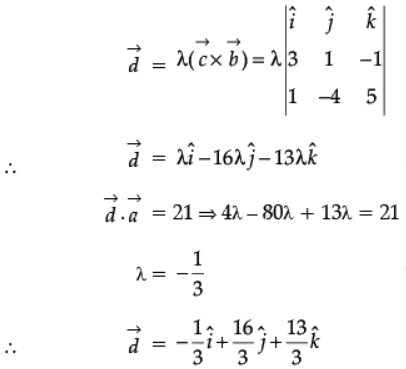
Q.30. Using vectors, find the area of the triangle whose vertices are A(1, 2, 3), B(2, – 1, 4) and C(4, 5, – 1).
Ans.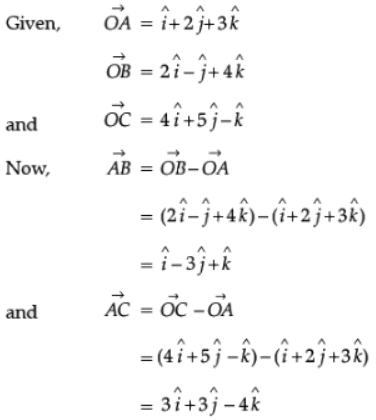
∴ The area of the given triangle

Q.31. Maximise Z = x + 2y
Subject to the constraints
x + 2y ≥ 100
2x – y ≤ 0
2x + y ≤ 200
x, y ≥ 0
Solve the above LPP graphically.
Ans.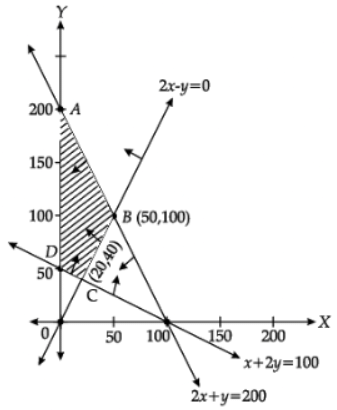 Z = x + 2y and x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200, x, y ≥ 0
Z = x + 2y and x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200, x, y ≥ 0
For correct graph of three lines
For correct shading ABCD
Z(A) = 0 + 400 = 400
Z(B) = 50 + 200 = 250
Z(C) = 20 + 80 = 100
Z(D) = 0 + 100 = 100
Max (Z = 400) at x = 0, y = 200
Q.32. Solve the following L.P.P. graphically:
Maximize Z = 100x + 120y
Subject to the constraints: 5x + 8y ≤ 200
10x + 8y ≤ 240
and x, y ≥ 0
Ans.
Given L.P.P. is:
Maximize Z = 100x + 120y
Subject to 5x + 8y ≤ 200
10x + 8y ≤ 240
and x, y ≥ 0
To solve the LPP graphically first we convert inequalities into equations and draw the corresponding lines.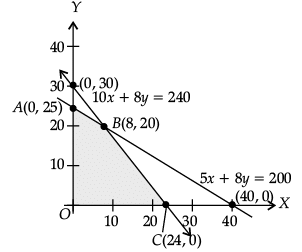
Then,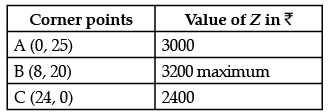
Clearly maximum value Z = 3200 is obtained at x = 8 and y = 20
OR
Solve the following L.P.P. graphically :
Maximize Z = 7x + 4y
Subject to the constraints: 3x + 2y ≤ 12
3x + y ≤ 9
and x, y ≥ 0
Ans.
Given L.PP is:
Maximise Z = 7x + 4y
Subject to constraints,
3x + 2y ≤ 12
3x + y ≤ 9
x ≥ 0, y ≥ 0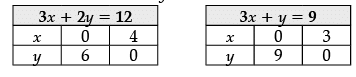
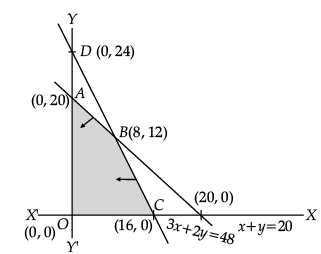
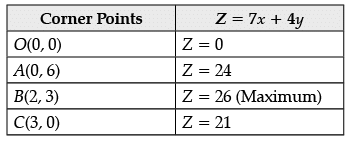
Hence max value Z = 26 is obtained at x = 2 and y = 3.
Q.33. Show that the relation R on the set Z of all integers defined by (x, y) ∈ R ⇔ (x – y) is divisible by 3 is an equivalence relation.
Ans. (x – x) = 0 is divisible by 3 for all x ∈ Z. So, (x, x) ∈ R
∴ R is reflexive
So (x, y) ∈ R implies (y, x) ∈ R, x, y ∈ Z
⇒ R is symmetric,
(x – y) is divisible by 3 and (y – z) is divisible by 3.
So (x – z) = (x – y) + (y – z) is divisible by 3.
∴ (x, z) ∈ R ⇒ R is transitive
Hence, R is an equivalence relation.
Q.34. A farmer has a field of shape bounded by x = y2 and x = 3, he wants to divide this into his two sons equally by a straight line x = c. Can you find c ?
Ans.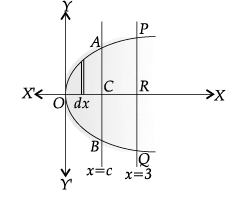
Given,
Area OACBO = Area of APRQBCA
or Area OACBO = 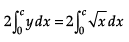
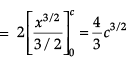
Area of APRQBCA = 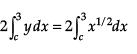
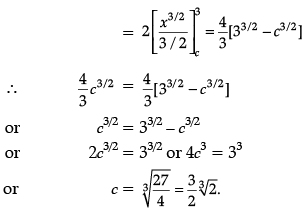
Q.35. In a shop X, 30 tins of ghee of type A and 40 tins of ghee of type B which look alike, are kept for sale. While in shop Y, similar 50 tins of ghee of type A and 60 tins of ghee of type B are there. One tin of ghee is purchased from one of the randomly selected shop and is found to be of type B. Find the probability that it is purchased from shop Y.
Ans. Suppose A : getting type B ghee
E1 : Ghee purchased from X
E2 : Ghee purchased from Y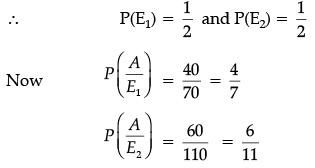
From Bayes' Theorem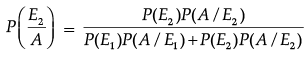
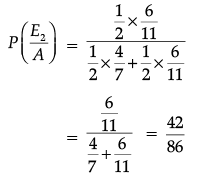
Therefore 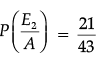
Section - V
Question numbers 36 to 38 carry 5 marks each.
Q.36. If length of three sides of a trapezium other than base are equal to 10 cm, then find the area of the trapezium when it is maximum.
Ans.
The required trapezium is as given in figure.
Draw perpendiculars DP and CQ on AB. Let AP = x cm. Note that ΔAPD ≌ ΔBQC.
Therefore, QB = x cm. Also, by Pythagoras theorem QP = 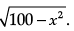
Let A be the area of the trapezium.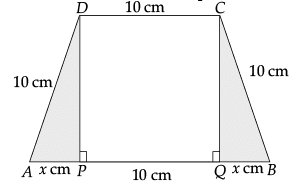
Then, A ≡ A(x)
= 1/2 (sum of parallel sides) × (height)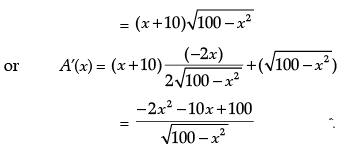
Now, A’(x) = 0 gives 2x2 + 10x – 100 = 0,
i.e., x = 5 and x = – 10.
So, x = 5.
Now, A”(x) =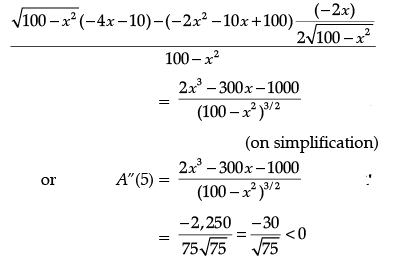
Thus, area of trapezium is maximum at x = 5 and the maximum area is given by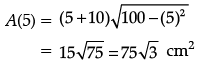
OR
Find the point on the curve y2 = 4x, which is nearest to the point (2, – 8).
Ans. Let P (x, y) be any point on the curve y2 = 4x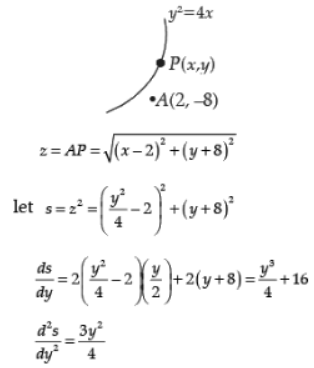
Let ds/dy = 0 ⇒ y3 = -64 ⇒ y = -4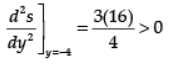
∴ s or z is minimum at y = –4; x = y2/4 = 4
∴ The nearest point is P(4, –4)
Detailed Solution:
The equation of the given curve is y2 = 4x
∴ x = y2/4 ...(i)
Let P(x, y) be a point on the curve, which is nearest to point A(2, – 8).
Now, distance between the points A and P is given by: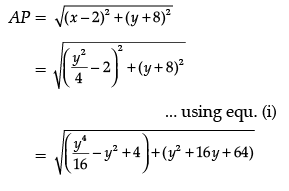
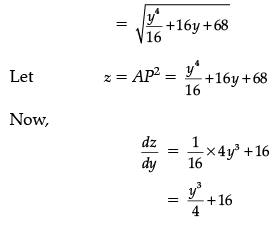
Fr maximum or minimum value of z, we have
dz/dy = 0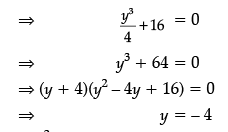
[∵ y2 – 4y + 16 = 0 gives imaginary values of y]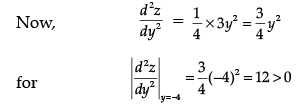
Thus, z is minimum when y = – 4
Substituting y = – 4 in the equation of the curve y2 = 4x, we obtain x = 4.
Hence, the point (4, – 4) on the curve y2 = 4x is nearest to the point (2, – 8).
Q.37. Find: 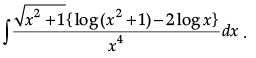
Ans.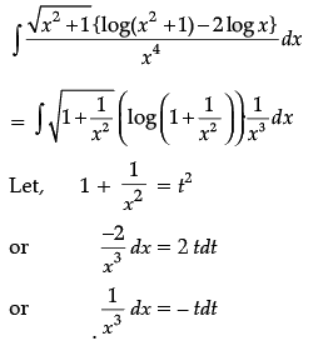
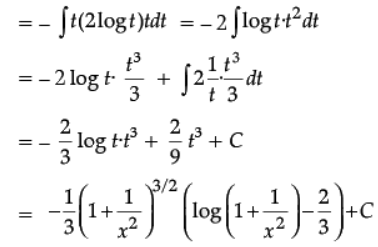
OR
Evaluate: 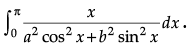
Ans.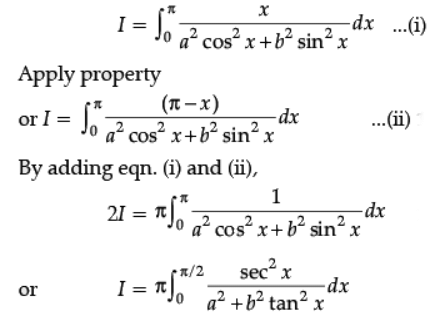
Dividing Nr. & Dr. by cos2x
Put b tan x = t or sec2 xdx = 1/b dt
When x = 0, t = 0;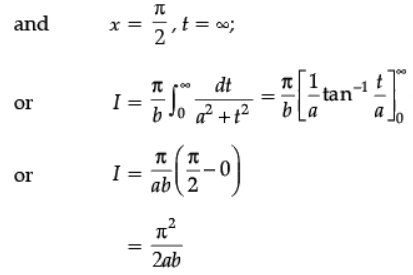
Q.38. Evaluate: 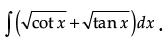
Ans.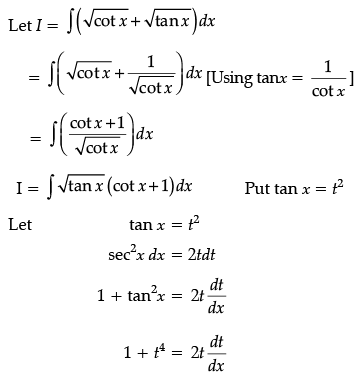
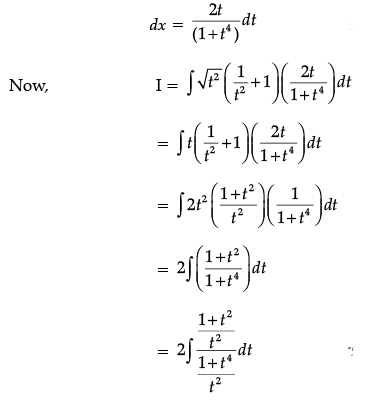
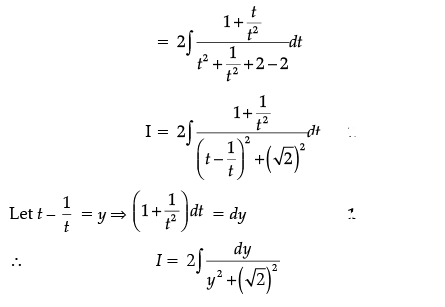
OR
Evaluate: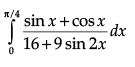
Ans.
Put sin x – cos x = t,
(cos x + sin x) dx = dt.
1 – sin 2x = t2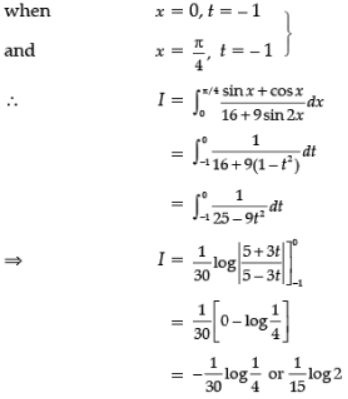
|
203 videos|307 docs|139 tests
|















