Trigonometric Ratios & Identities- 2 | Mathematics (Maths) for JEE Main & Advanced PDF Download
Trigonometric Ratios of the Sum & Difference of Two Angles
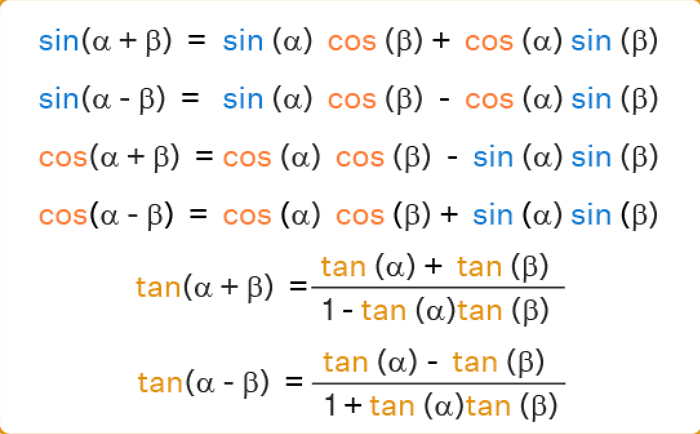
➢ Some More Results
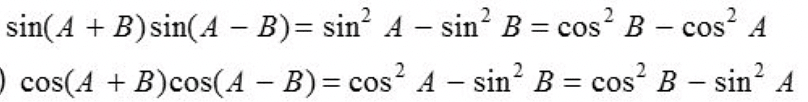
Solved Examples
Example.5. Prove that √3 cosec20° – sec20° = 4.
Solution. L.H.S.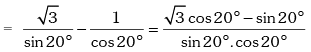
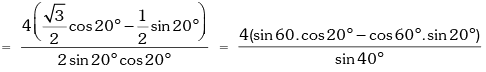
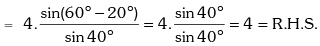
Example.6. Prove that tan70° = cot70° + 2cot40°.
Solution. L.H.S.
= tan70° = tan (20° + 50°)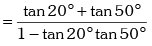
or tan70° – tan20° tan50° tan70° = tan20° + tan50°
or tan70° = tan70° tan50° tan20° + tan20° + tan50° = 2 tan 50° + tan20°
= cot70° + 2cot40° = R.H.S.
Formulas to Transform the Product into Sum or Difference

Example.7. If sin2A = λ sin2B, then prove that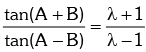
Solution. Given sin2A = λ sin2B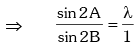
Applying componendo & dividendo,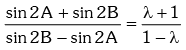
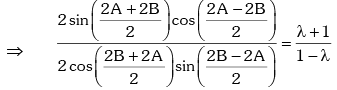
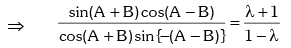
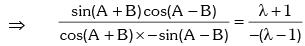
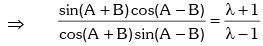
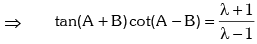
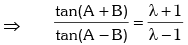
Formulas to Transform Sum or Difference into Product
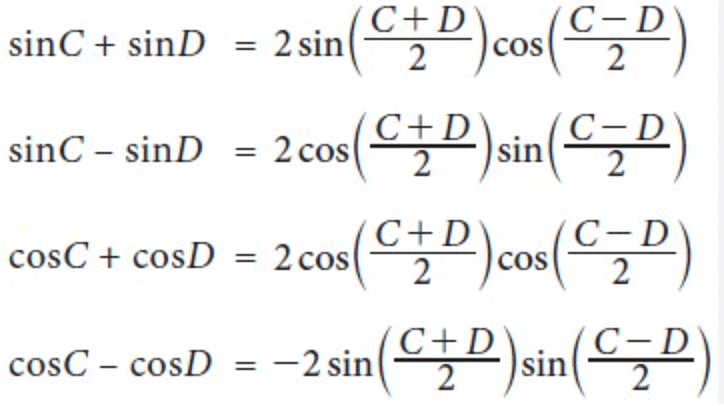
Example.8.
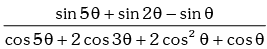 is equal to:
is equal to:(a) tan θ
(b) cos θ
(c) cot θ
(d) none of these
Ans. (a)
Solution. L.H.S.
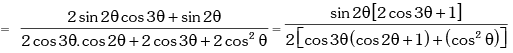
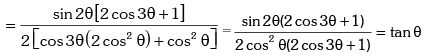
Example.9. Show that sin12º .sin48º .sin54º = 1 / 8
Solution. L.H .S.
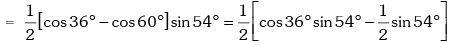
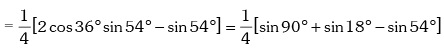
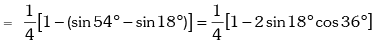
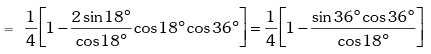
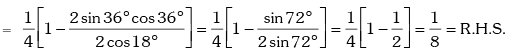
Trigonometric Ratios of sum of more than two angles
(i) sin (A + B + C) = sinAcosBcosC + sinBcosAcosC + sinCcosAcosB – sinAsinBsinC
= ΣsinA cosB cosC – Πsin A
cosA cosB cosC [tanA + tanB + tanC - tanA tanB tanC]
(ii) cos (A + B + C) = cosA cosB cosC – sinA sinB cosC – sinA cosB sinC – cosA sinB sinC
= Πcos A - Σsin A sin B cos C
= cos A cos B cos C [1 - tan A tan B - tan B tan C - tan C tan A]
(iii) tan (A + B + C) =
Trigonometric Ratios of Multiple Angles
(a) Trigonometrical ratios of an angle 2θ in terms of the angle θ :
(i) sin 2θ = 2 sin θ cos θ =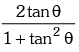
(ii) cos 2θ = cos2θ - sin2θ = 2 cos2θ - 1 = 1 - 2 sin2θ =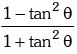
(iii) 1 + cos 2θ = 2 cos2 θ
(iv) 1 - cos 2θ = 2 sin2 θ
(v)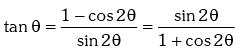
(vi)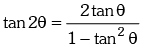
Example.10. Prove that :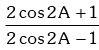 = tan (60º + A) tan (60º - A)
= tan (60º + A) tan (60º - A)
Solution. R.H.S. = tan(60° + A) tan(60° – A)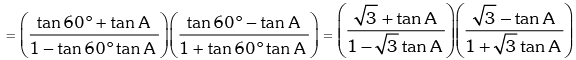
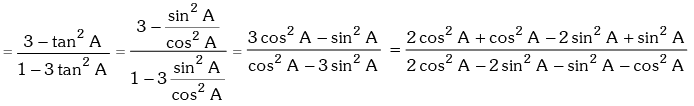
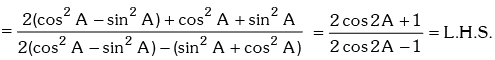
(b) Trigonometrical ratios of an angle 3θ in terms of the angle θ :
(i) sin3θ = 3sinθ - 4sin3θ.
(ii) cos3θ = 4cos3θ - 3cosθ.
(iii)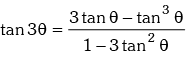
Example.11. Prove that : tanA + tan(60° + A) + tan(120° + A) = 3tan3A
Solution. L.H.S. = tanA + tan(60° + A) + tan(120° + A)
= tanA + tan(60° + A) + tan{180° –(60° – A)}
= tanA + tan(60° + A) – tan(60° – A) [∵ tan(180° - θ) = -tanθ]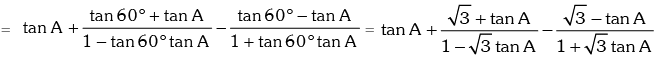
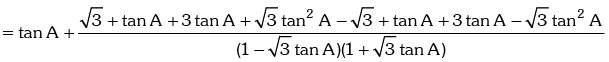
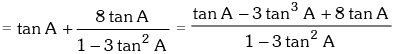

Trigonometric Ratios of Sub Multiple Angles
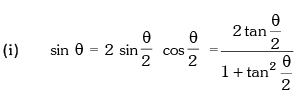
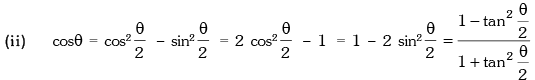
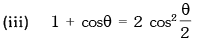
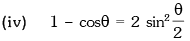
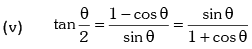
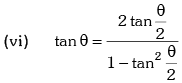
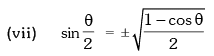
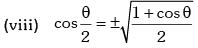
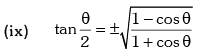
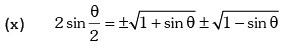
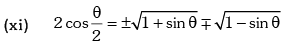
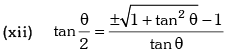
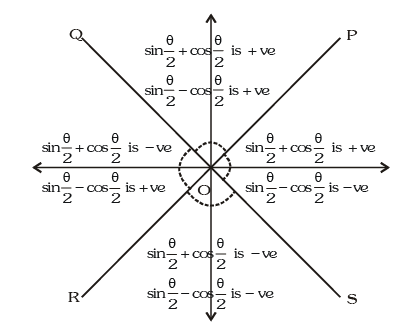
Example.12.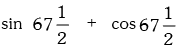 is equal to
is equal to
(a)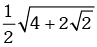
(b)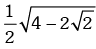
(c)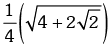
(d)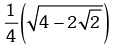
Ans. (a)
Solution. 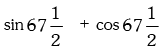
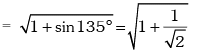
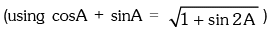
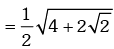
Trigonometric Ratios of Some Standard Angles
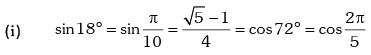
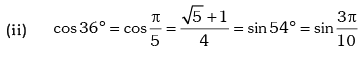
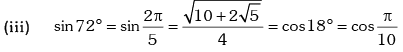
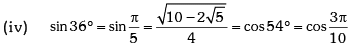
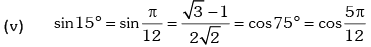
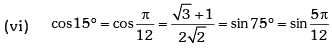
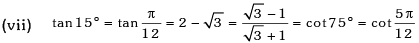
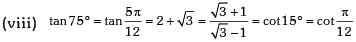
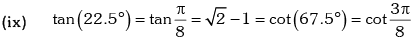

Example.13. Evaluate sin78 ° – sin66 ° – sin42 ° + sin 6°.
Solution. The expression = (sin78° - sin42°) - (sin66° - sin6°) = 2cos(60°) sin(18°) - 2cos36° . sin30°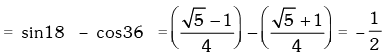
Conditional Trigonometric Identities
If A + B + C = 180°, then
(i) tan A + tan B + tan C = tan A tan B tan C
(ii) cot A cot B + cot B cot C + cot C cot A = 1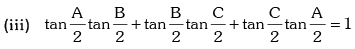
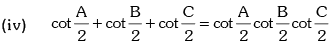
(v) sin 2A + sin 2B + sin 2C = 4 sinA sinB sinC
(vi) cos 2A + cos 2B + cos 2C = –1 – 4 cosA cosB cosC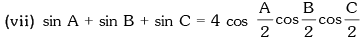
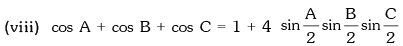
Example.14. In any triangle ABC, sin A – cos B = cos C, then angle B is
(a) π / 2
(b) π / 3
(c) π / 4
(d) π / 6
Ans. (a)
Solution. We have, sin A – cos B = cos C
sin A = cos B + cos C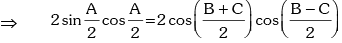
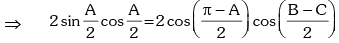 ∵ A + B + C = π
∵ A + B + C = π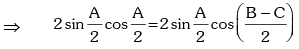
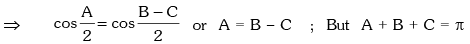
Therefore 2B = π ⇒ B = π / 2
Example.15. If A + B + C = 3π / 2, then cos 2A + cos 2B + cos2C is equal to
(a) 1 – 4cosA cosB cosC
(b) 4 sinA sin B sinC
(c) 1 + 2cosA cosB cosC
(d) 1 – 4 sinA sinB sinC
Ans. (d)
Solution. cos 2A + cos 2B + cos 2C = 2 cos (A + B ) cos (A – B) + cos 2C
=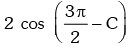 cos (A – B) + cos 2C ∵ A + B + C = 3π / 2
cos (A – B) + cos 2C ∵ A + B + C = 3π / 2
= – 2 sin C cos ( A– B) + 1 – 2 sin2C = 1 – 2 sinC [ cos ( A– B) + sin C)
= 1 – 2 sin C [ cos (A – B) + sin
= 1 – 2 sin C [ cos (A – B) – cos ( A +B ) ]
= 1 – 4 sin A sin B sin C
Maximum & Minimum Values of Trigonometric Expressions
(i) acosθ + bsinθ will always lie in the interval 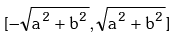 i.e. the maximum and minimum values are
i.e. the maximum and minimum values are 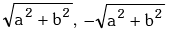 respectively.
respectively.
(ii) Minimum value of a2 tan2 θ + b2 cot2 θ = 2ab where a, b > 0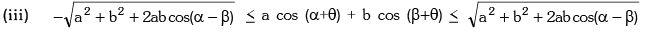 where α and β are known angles.(iv)
where α and β are known angles.(iv)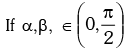 and α + β = s (constant) then
and α + β = s (constant) then
(a) Maximum value of the expression cos α cos β, cos α + cos β, sin α sin β or sin α + sin β occurs when α = β = a / 2
(b) Minimum value of sec α + sec β, tanα + tanβ, cosec α + cosec β occurs when α = β = a / 2
(v) If A, B, C are the angles of a triangle then the maximum value of
sin A + sin B + sin C and sin A sin B sin C occurs when A = B = C = 60
(vi) In case a quadratic in sin θ & cos θ is given then the maximum or minimum values can be obtained by making a perfect square.
Example.16. Prove that: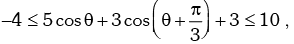 for all values of θ.
for all values of θ.
Solution. We have,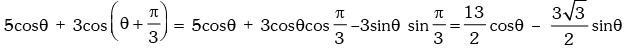
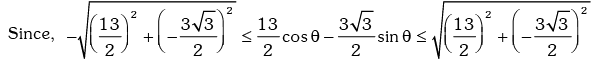
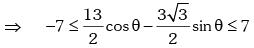
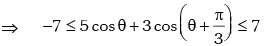 for all θ.
for all θ.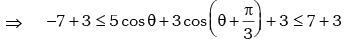 for all θ.
for all θ.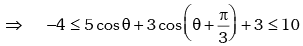 for all θ.
for all θ.
Example.17. Find the maximum value of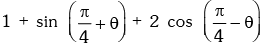
(a) 1
(b) 2
(c) 3
(d) 4
Ans. (d)
Solution. We have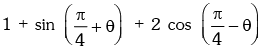
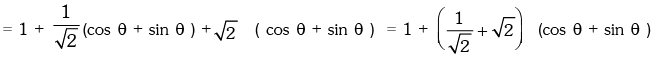
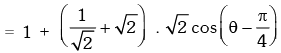
∴ maximum value =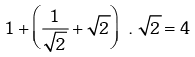
Important Results
(i) sinθ sin (60° – θ) sin (60° + θ) =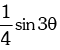
(ii) cosθ. cos (60° - θ) cos (60° + θ) =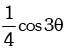
(iii) tanθ tan (60° - θ) tan (60° + θ) = tan 3θ
(iv) cot θ cot (60° - θ) cot (60° + θ) = cot 3θ
(v) (a) sin2 θ + sin2 (60° + θ) + sin2 (60° - θ) = 3 / 2
(b) cos2 θ + cos2 (60° + θ) + cos2 (60° - θ) = 3 / 2
(vi) (a) If tan A + tan B + tan C = tan A tan B tan C, then A + B + C = nπ, n ∈ I
(b) If tan A tan B + tan B tan C + tan C tan A = 1, then A + B + C = (2n + 1) π / 2, n ∈ I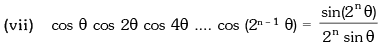
(viii) (a) cotA – tanA = 2cot2A
(b) cotA + tanA = 2cosec2A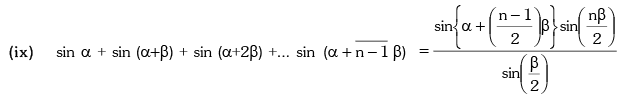
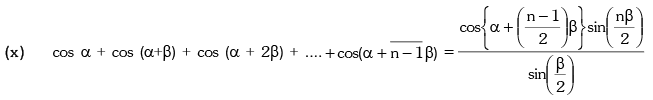
Example.18. Prove that tanA + 2tan2A + 4tan4A + 8cot8A = cot A.
Solution. 8 cot 8A = cotA - tanA - 2tan2A - 4tan4A
= 2 cot2A - 2tan2A - 4tan4A (using viii (a) in above results)
= 4 cot4A - 4tan4A (using viii (a) in above results)
= 8 cot8A.
Alternate Method:
L.H.S. = tanA + 2tan2A + 4tan4A +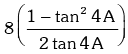
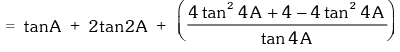
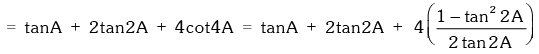
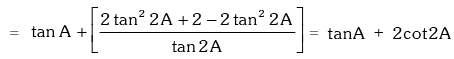
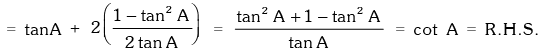
Example.19. Evaluate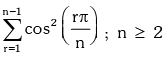
Solution.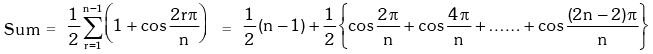

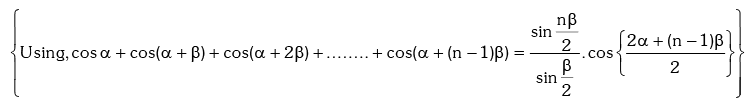
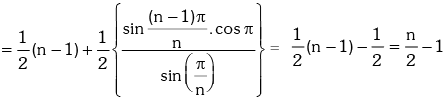
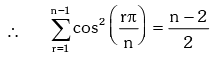
Example.20. Prove that : (1 + sec2θ)(1 + sec22θ)(1 + sec23θ)....(1 + sec2nθ) = tan2nθ.cotθ.
Solution. L.H.S.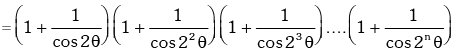
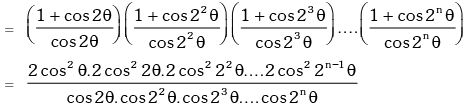

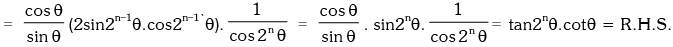
Miscellaneous Illustration
Example.21. Prove that
tanα + 2 tan2α + 22 tan2α + . .. .. . + 2n - 1 tan 2n - 1 α + 2n cot2nα = cot α
Solution. We know tanθ = cotθ - 2 cot 2θ .....(i)
Putting 0 = a, 2α, 22α,.....in (i), we get
tan α = (cot α - 2 cot 2α)
2 (tan 2 α) = 2(cot 2α - 2 cot 22α)
22 (tan 22α) = 22 (cot 22α - 2 cot 23α)
...........................................................
2n - 1 (tan 2n - 1α) = 2n - 1 (cot 2n - 1α - 2 cot 2nα)
Adding,
tan α + 2 tan2α + 22 tan2α +....+ 2n-1 tan 2n-1α = cot a - 2n cot 2nα
∴ tan α + 2 tan2 α + 22 tan2α +....+ 2n-1 tan 2n-1 a + 2n cot 2n a = cot α
Example.22. If A,B,C and D are angles of a quadrilateral and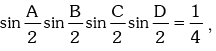 prove that A = B = C = D = π / 2.
prove that A = B = C = D = π / 2.
Solution. 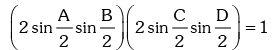
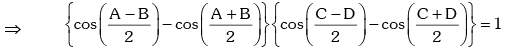
Since, A + B = 2π - (C + D), the above equation becomes,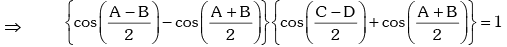
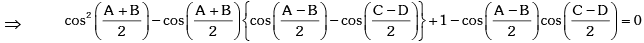
This is a quadratic equation in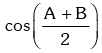 which has real roots .
which has real roots .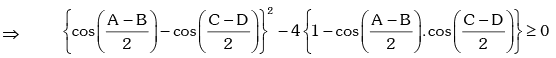
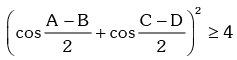

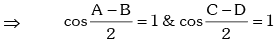
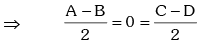
⇒ A = B , C = D .
Similarly A = C, B = D ⇒ A = B = C = D = π / 2
|
172 videos|503 docs|154 tests
|
FAQs on Trigonometric Ratios & Identities- 2 - Mathematics (Maths) for JEE Main & Advanced
| 1. What are the trigonometric ratios of the sum and difference of two angles? |  |
| 2. What are the formulas to transform a product into a sum or difference of two angles? |  |
| 3. What are the formulas to transform a sum or difference of two angles into a product? |  |
| 4. What are the trigonometric ratios of the sum of more than two angles? |  |
| 5. What are the trigonometric ratios of multiple angles? |  |





















