RS Aggarwal Solutions: Exercise 1F - Number System | Extra Documents & Tests for Class 9 PDF Download
Q.1. Write the rationalising factor of the denominator in 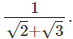
Ans.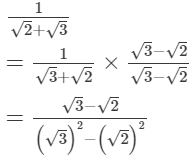
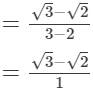
Here, the denominator i.e. 1 is a rational number. Thus, the rationalising factor of the denominator in 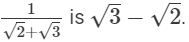
Q.2. Rationalise the denominator of each of the following.
(i)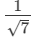
(ii)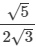
(iii)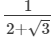
(iv)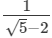
(v)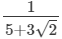
(vi)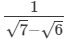
(vii)
(viii)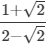
(ix)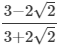
Ans.
(i)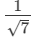
On multiplying the numerator and denominator of the given number by √7, we get: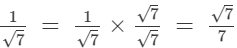
(ii)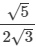
On multiplying the numerator and denominator of the given number by √3, we get: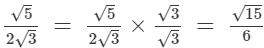
(iii)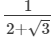
On multiplying the numerator and denominator of the given number by 2 - √3, we get: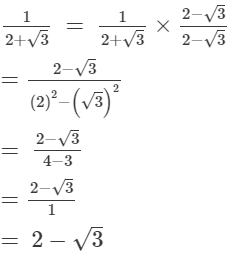
(iv)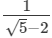
On multiplying the numerator and denominator of the given number by √5 +2, we get:
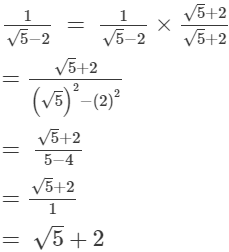
(v)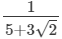
On multiplying the numerator and denominator of the given number by 5-3√2, we get: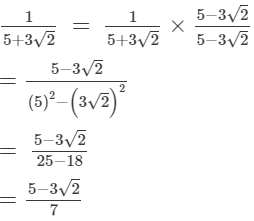
(vi)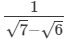
Multiplying the numerator and denominator by √7+√6, we get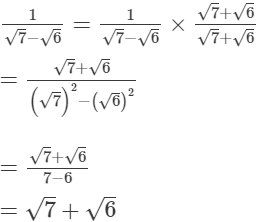
(vii)
Multiplying the numerator and denominator by √11+√7, we get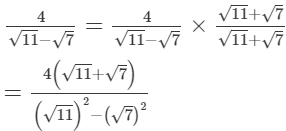
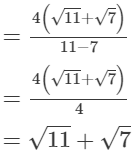
(viii)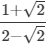
Multiplying the numerator and denominator by 2+√2, we get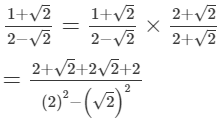
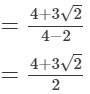
(ix)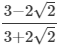
Multiplying the numerator and denominator by 3-2√2, we get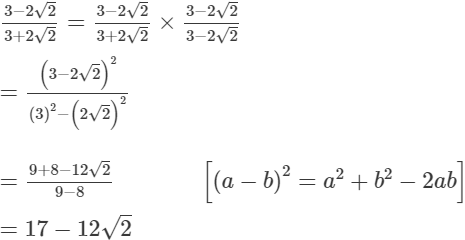
Q.3. It being given that √2 = 1.414, √3 = 1.732, √5 = 2.236 and √10 = 3.162, find the value of three places of decimals, of each of the following.
(i)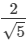
(ii)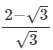
(iii)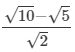
Ans.
(i)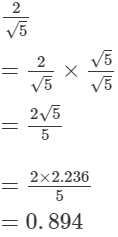
(ii)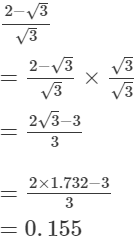
(iii)
Q.4. Find rational numbers a and b such that
(i)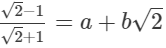
(ii)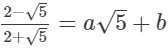
(iii)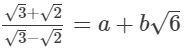
(iv)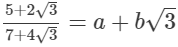
Ans.
(i)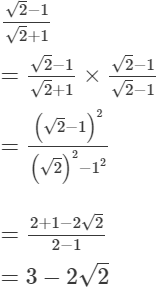
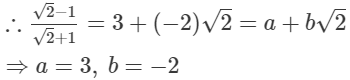
(ii)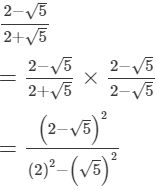
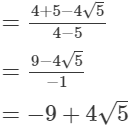
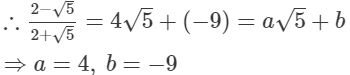
(iii)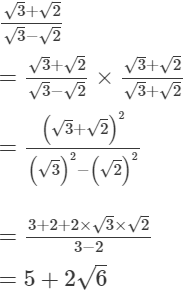

(iv)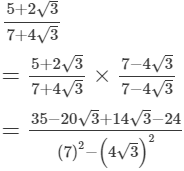

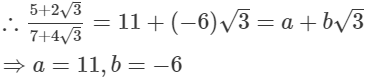
Q.5. It being given that √3 = 1.732, √5 = 2.236, √6 = 2.449 and √10 = 3.162, find to three places of decimal, the value of each of the following.
(i)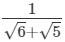
(ii)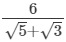
(iii)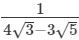
(iv)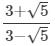
(v)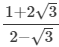
(vi)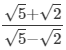
Ans.
(i)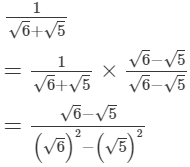
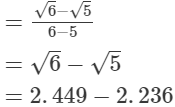
= 0.213
(ii)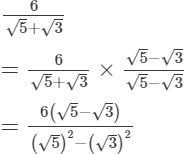

=3 × (2.236 − 1.732)
= 1.512
(iii)
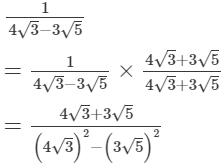
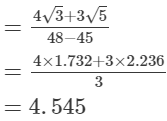
(iv)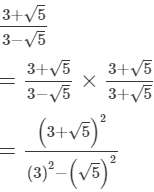
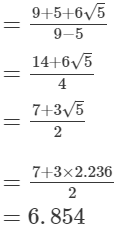
(v)
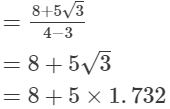
= 16.660
(vi)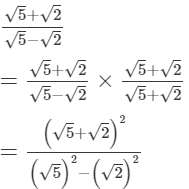
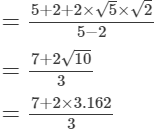
= 4.441
Q.6. Simplify by rationalising the denominator.
(i)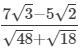
(ii)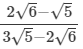
Ans.
(i)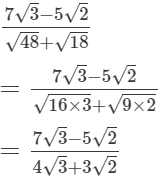
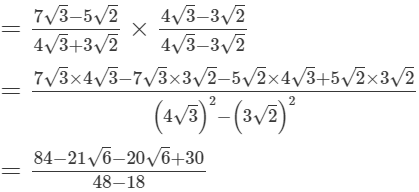
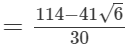
(ii)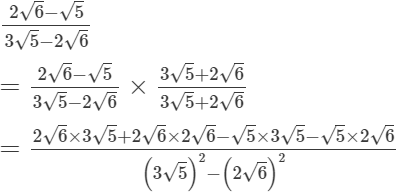

Q.7. Simplify
(i)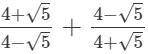
(ii)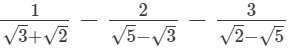
(iii)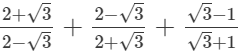
(iv)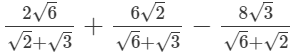
Ans.
(i)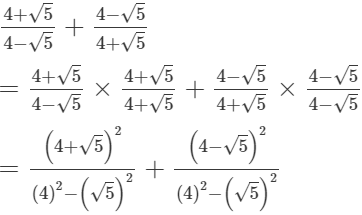
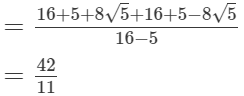
(ii)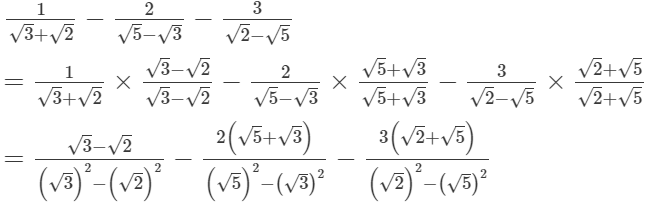
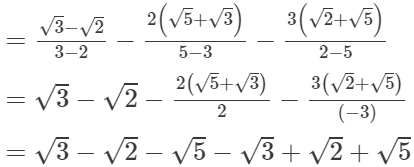
= 0
(iii)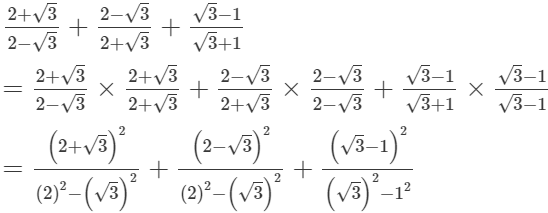
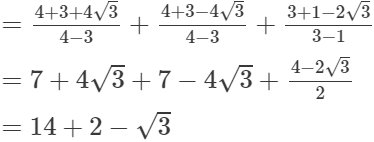
= 16 − √3
(iv)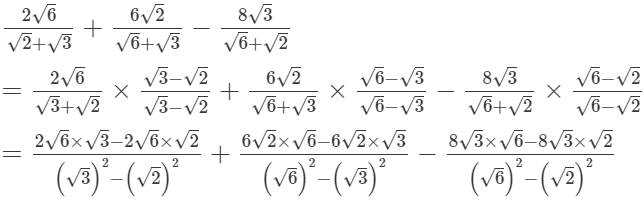
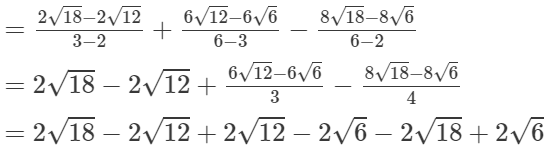
= 0
Q.8. Prove that
(i)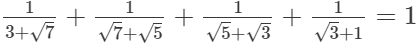
(ii)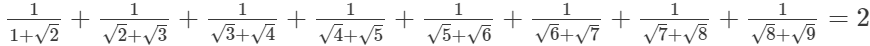
Ans.
(i)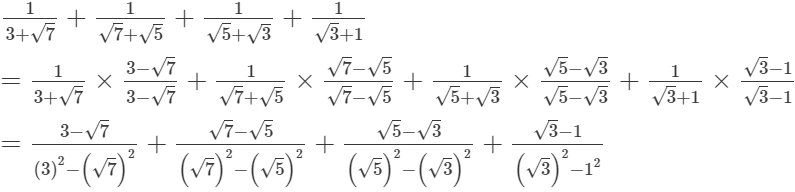
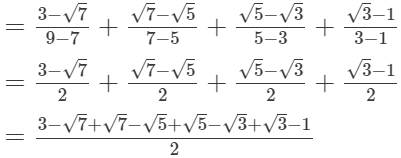
= 2/2
= 1
(ii)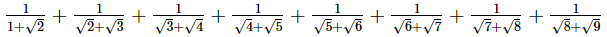
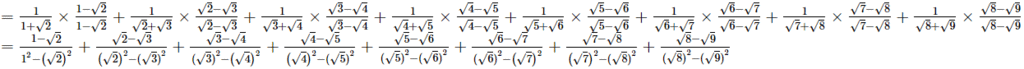
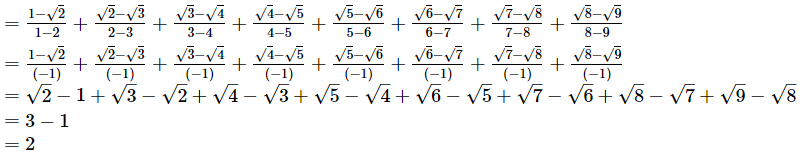
Q.9. Find the values of a and b if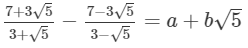
Ans.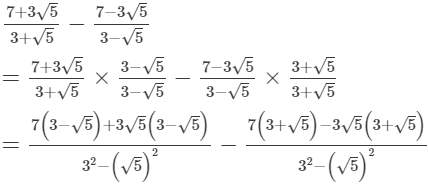
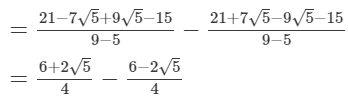

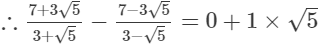
Comparing with the given expression, we get
a = 0 and b = 1
Thus, the values of a and b are 0 and 1, respectively.
Q.10. Simplify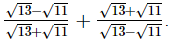
Ans.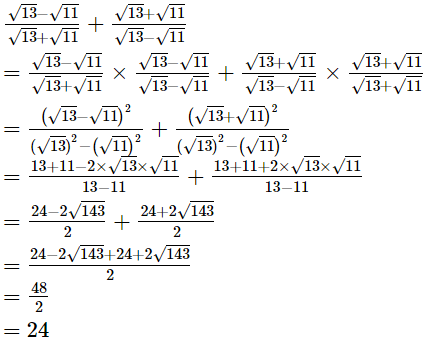
Q.11. If x = 3 + 2√2, check whether 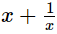 is rational or irrational.
is rational or irrational.
Ans.
x = 3 + 2√2 .....(1)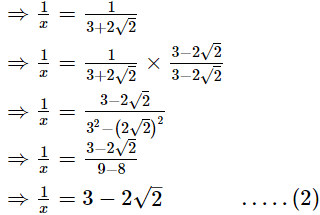
Adding (1) and (2), we get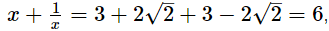 which is a rational number
which is a rational number
Thus,  is rational.
is rational.
Q.12.
If x = 2 − √3, find value of 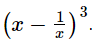
Ans.
x = 2 − √3 .....(1)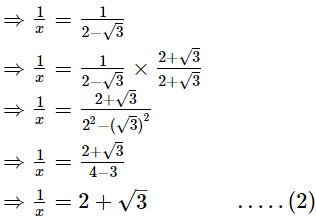
Subtracting (2) from (1), we get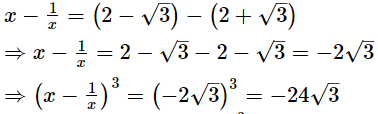
Thus, the value of 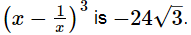
Q.13. If x = 9 − 4√5, find the value of 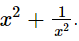
Ans.
x = 9 − 4√5 .....(1)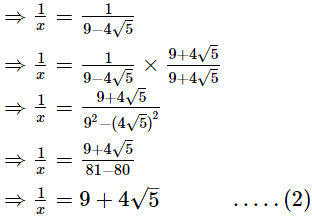
Adding (1) and (2), we get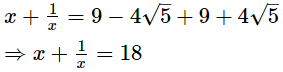
Squaring on both sides, we get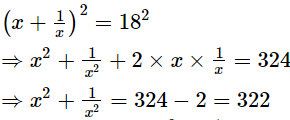
Thus, the value of x2 + 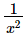 is 322.
is 322.
Q.14. If x = 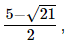 find the value of
find the value of 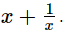
Ans.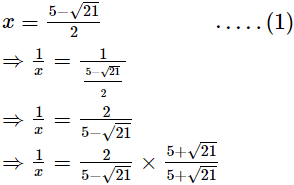
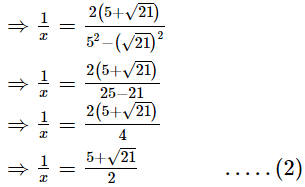
Adding (1) and (2), we get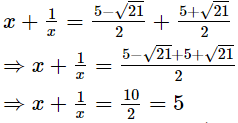
Thus, the value of x +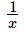 is 5.
is 5.
Q.15. If a = 3 − 2√2, find the value of a2 - 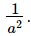
Ans.
a = 3−2√2
⇒ a2 = (3−2√2)2
⇒ a2 = 9 + 8 − 12√2
⇒ a2 = 17 − 12√2 .....(1)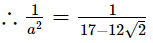
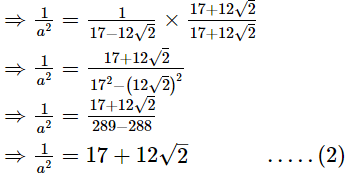
Subtracting (2) from (1), we get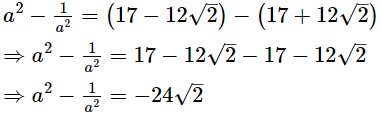
Thus, the value of a2 - 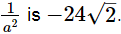
Q.16. If x = √13 + 2√3, find the value of x − 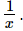
Ans.
Subtracting (2) from (1), we get
Thus, the value of x 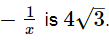
Q.17.
If x = 2 + √3, find the value of 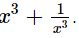
Ans.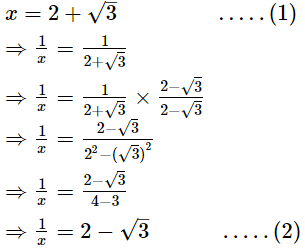
Adding (1) and (2), we get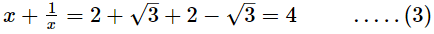
Cubing both sides, we get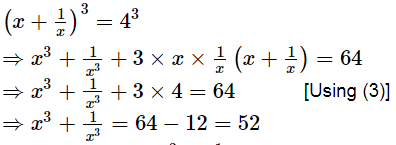
Thus, the value of 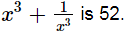
Q.18. If 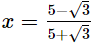 and
and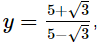 show that
show that 
Ans.
Disclaimer: The question is incorrect.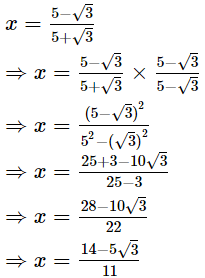
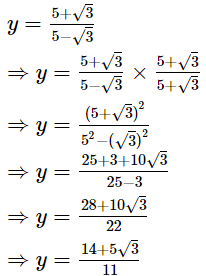
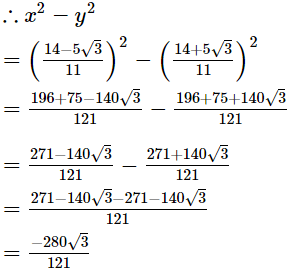
The question is incorrect. Kindly check the question.
The question should have been to show that x − y = 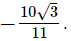
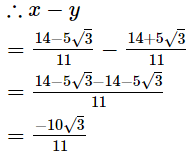
Q.19. If a = 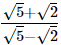 and b =
and b = 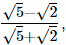 show that 3a2 + 4ab − 3b2 =
show that 3a2 + 4ab − 3b2 = 
Ans.
According to question,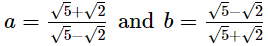
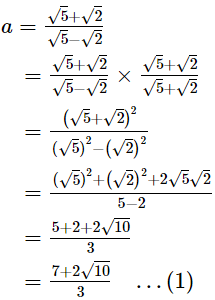
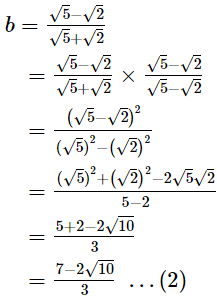
Now,
3a2 + 4ab − 3b2
= 3(a2 − b2) + 4ab
= 3 (a + b)(a − b) + 4ab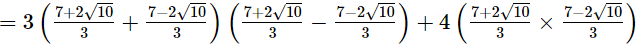

Hence, 3a2 + 4ab − 3b2 = 
Q.20.
If a = 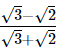 and b =
and b =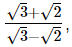 find the value of a2 + b2 – 5ab.
find the value of a2 + b2 – 5ab.
Ans.
According to question,
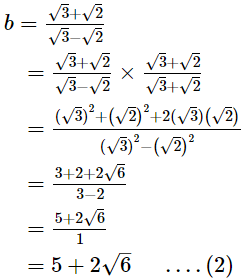
Now,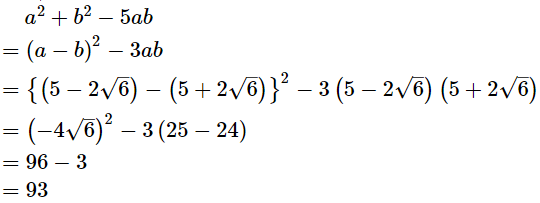
Hence, the value of a2 + b2 – 5ab is 93.
Q.21.
If p = 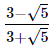 and q =
and q = 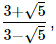 find the value of p2 + q2.
find the value of p2 + q2.
Ans.
According to question,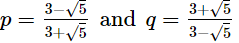
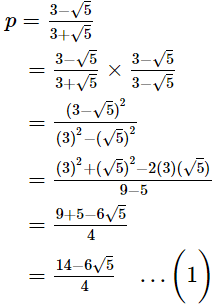
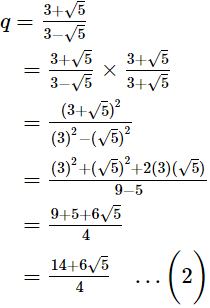
Now,
p2 + q2 = (p+q)2 − 2pq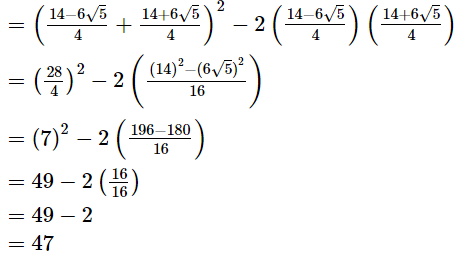
Hence, the value of p2 + q2 is 47.
Q.22. Rationalise the denominator of each of the following.
(i)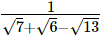
(ii) 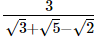
(iii)
Ans.
(i)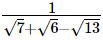

Hence, the rationalised form is 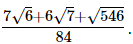
(ii) 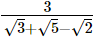
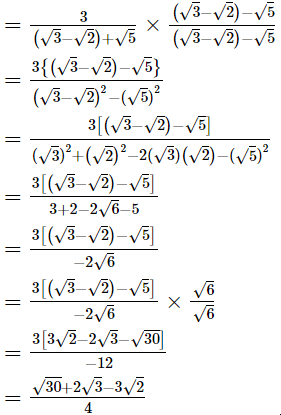
Hence, the rationalised form is 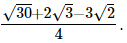
(iii) 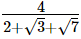

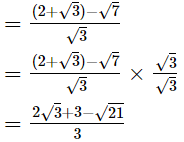
Hence, the rationalised form is 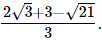
Q.23. Given, √2 = 1.414 and √6 = 2.449, find the value of 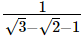 correct to 3 places of decimal.
correct to 3 places of decimal.
Ans.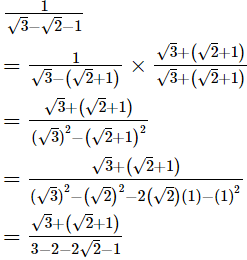
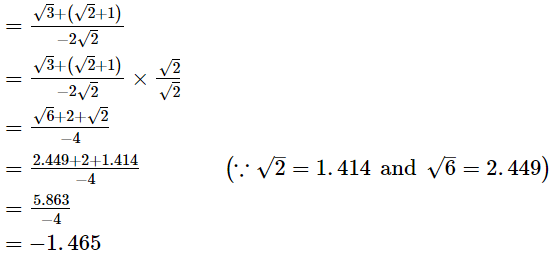
Hence, the value of  correct to 3 places of decimal is −1.465.
correct to 3 places of decimal is −1.465.
Q.24. If x = 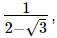 find the value of x3 – 2x2 – 7x + 5.
find the value of x3 – 2x2 – 7x + 5.
Ans.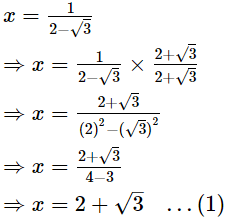
Now,
Also,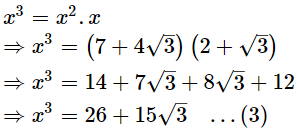
Now,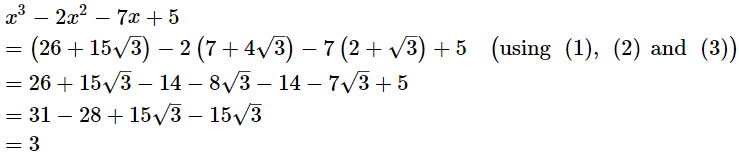
Hence, the value of x3 – 2x2 – 7x + 5 is 3.
Q.25. Evaluate 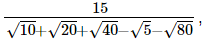 it being given that √5 = 2.236 and √10 = 3.162.
it being given that √5 = 2.236 and √10 = 3.162.
Hint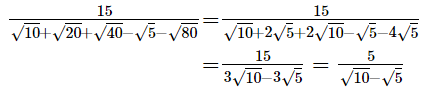
Ans.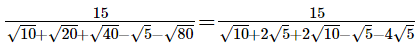
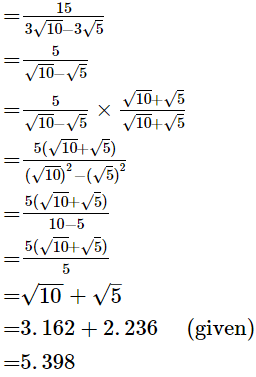
Hence,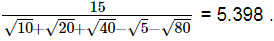
|
1 videos|228 docs|21 tests
|
















