Flood Estimation & Flood Routing | Engineering Hydrology - Civil Engineering (CE) PDF Download
Floods, Flood Routing and Flood Control
A flood an unusually high stage in a river, normally the level at which the river overflow its banks and inundates the adjoining area. The design of bridges, culvert waterways and spillways for dams and estimation of score at a hydraulic structure are some examples wherein flood-peak values are required.
To estimate the magnitude of a flood peak the following alternative methods are available:
- Rational method
- Empirical method
- unit-hydrograph technique
- Flood-frequency studies
- Rational Method
If tp ≥ tc
Qp = 1 / 36.k.Pc.A
Where, Qp = Peak discharge in m3/sec
PC = Critical design rainfall in cm/hr
A = Area catchment in hectares
K = Coefficient of runoff.
tD = Duration of rainfall
tC = Time of concentration - Empirical Formulae
(i) Dickens Formula (1865)
Where, Qp = Flood peak discharge in m3/sec
A = Catchment area in km2.
CD = Dickens constant, 6 ≤ CD ≤ 30.
(ii) Ryve’s formula (1884)
QP = CR.A2/3
Where,
CH = Ryve’s constant
= 8.8 for constant area within 80 km from the cost.
= 8.5 if distance of area is 80 km to 160 km from the cost.
= 10.2 if area is Hilley and away from the cost.
(iii) Inglis Formula (1930)
Where, A = Catchment area in Km2.
QP = Peak discharge in m3/sec. - Flood Frequency Studies
(i) Recurrence interval or return Period:
T = 1/P where, P = Probability of occurrence
(ii) Probability if non-occurrence: q = 1 - P
(iii) Probability of an event occurring r times in ‘n’ successive years: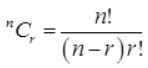 (iv) Reliability: (probability of non-occurrence /Assurance) = qn
(iv) Reliability: (probability of non-occurrence /Assurance) = qn
(v) Risk = 1 - qn → Risk = 1(1 - P)n
(vi) Safety Factory = Design values of hydrologic parameter adopted / Estimated value of hydrological parameter
(vii) Safety Margin = design value of hydrological parameter – Estimated value of hydrological parameter
Gumbel’s Method
The extreme value distribution was introduction by Gumbel (1941) and is commonly known as Gumbel’s distribution. it is one of the most widely used probability distribution functions for extreme values in hydrologic and meteorologic studies for prediction of flood peaks, maximum rainfall, maximum wind speed.
Gunbel defined a flood as the largest of the 365 daily flows and the annual series of flood flows constitute a series of largest values of flows.
Based on probability distribution.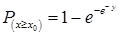
 Where, XT = Peak value of hydrologic data
Where, XT = Peak value of hydrologic data
K = Frequency factor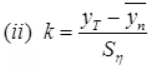
yT = Reduced variate
yr = -log∈log∈(T / T - 1)
T = Recurrence interval in year
yn = Reduced mean = 0.577
Sn = Reduced standard deviation.
Sn = 1.2825 for N → ∞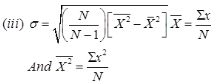
Confidence Limit
Since the value of the variate for a given return period, xT determined by Gumbel’s method can have errors due to the limited sample data used. An estimate of the confidence limits of the estimates is desirable the confidence interval indicates the limits about the calculated value between which the true value can be said to lie with specific probability based on sampling errors only.
For a confidence probability c, the confidence interval of the variate xT is bounded by value x1 and x2 given by
X2 / X1 = XT ± f(c) . S∈
Where, f(c) is a function of confidence probability ‘C’.
Se = Probability error
Where, N = Sample size
B = factor
σ = Standard deviation
Flood Routing
Flood routing is the technique of determining the flood hydrograph at a section of a river by utilizing the data of flood flow at one or more upstream sections. The hydrologic analysis of problems such a flood forecasting. Flood protection Reservoir design and spillway design invariable includes flood routing.
- Prism Storage: it is the volume that would exist if the uniform flow occurred at the downstream depth. i.e., the volume formed by an imaginary plane parallel to the channel bottom drawn at the outflow section water surface.
- Wedge Storage: it is the wedge like volume formed between the actual water surface profile and the top surface of the prism storage.
- Flood Routing
Muskingum Method
S = Sp + Sw
Where, S = Total storage in the channel.
Sp = Prism storage
= if (Q) = function of outflow discharge.
Sw = Wedge storage
= f(I) = function of inflow discharge.
S = f(Q)+f(I)S=k[XIm + (1-X)Qm]
Where, X = Weighting factor
M = Constant = 0.6 for rectangular channels
= 1.0 for nature channels
K = storage time constant
Method of Channel Routing
Muskingum Method: Hydrologic channel Routing
where, ΔS → Change in storage in time Δt
Δt → Time interval at which observations are taken. (Routing interval)
i → Avg. in flow rate over the period Δt
Average outflow rate over time period Δt.
- S1 = k[XI1 + (1 - X)Q1]
- S2 = k[XI2 + (1 - X)Q2]
- (S2 - S1) = k[X(I2 - X1)+(1 - X)(Q2 - Q1)]
- Q1 = Q1
- Q2 = C0I2 + C1I1 + C2Q1
- Qn = C0In + C1In-1 + C2Qn-1
Where, C0, C1 and C2, are Muskingum constant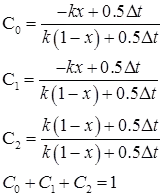
- for best result, 2Kx < Δt < k
Synthetic Hydrograph
Synder’s Method: Synder (1938), based on a study of a large number of catchment in the Appalachian Highlands of eastern United states developed a set of empirical equations for synthetic unit hydrograph in those areas .These equations are in use in the USA. And with some modifications in many other countries, and constitute what is known as Synder’s synthetic unit hydrograph.
(i) tP = Ct[L.LCa]0.3
Where, tp = Time interval between mid-point of unit rainfall excess and peak of unity hydrograph in hour
L = Length of main stream
LCa = The distance along the main stream from the basin outlet to a point on the stream which is nearest to the centrod of basis (in KM)
Ct = Regional constant 0.3 < Ct 0.6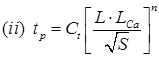 S = Basin slope.
S = Basin slope.
N = Constant = 0.38.
(iii) tr = tp / 5.5 tr = Standard duration of U.H in hour
(iv) QPS = 2.78CPA / tP
Where, Cp = Regional constant = 0.3 to 0.92.
A = Area of catchment in km2.
QPS = Peak discharge in m3/s.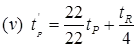 where, tR = standard rainfall duration.
where, tR = standard rainfall duration.
tP = Basin lag for non-standard U.H.
(vi) Qp = 2.78CPA / tP
(vii) tB = (72 + 3tP) hour, for a large catchment.
Where, tB = Base time of synthetic U.H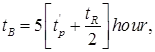 for small catchment.
for small catchment.
(viii) W50 = 5.87 / (q)1.08 W50 = width of U.H in hour at 50% peak discharge.
(ix) W75 = W50 / 7.15 W75 = Width of U.H in hours at 75% peak discharge.
(x) q = QP / A where, QP = Peak discharge in m3/sec.
A = Area in km2.
|
20 videos|53 docs|30 tests
|
FAQs on Flood Estimation & Flood Routing - Engineering Hydrology - Civil Engineering (CE)
| 1. What is flood estimation? |  |
| 2. What is flood routing? |  |
| 3. How does flood control work? |  |
| 4. What are the key factors considered in flood estimation? |  |
| 5. How does flood routing help in flood management? |  |
















