Water Requirements of Crops | Irrigation Engineering - Civil Engineering (CE) PDF Download
Water Requirements of Crops
Every crop requires a certain quantity of water after a certain fixed interval, throughout its period of growth. If natural rain is sufficient and timely so as to satisfy both these requirements, no irrigation water is required for raising that crop.
In a tropical country like India, the natural rainfall is either insufficient, or the water does not fall frequency of the rainfall varies throughout a tropical country, the certain crop may require irrigation in a certain part of the country. The area where irrigation is a must for agriculture is called the arid region, while the area in which inferior crops can be grown without irrigation is called a semiarid region.
- Crop Period or Base Period
The time period that elapses from the instant of its sowing to the instant of its harvesting is called the crop period.
The time between the first watering of a crop at the time of its sowing to its last watering before harvesting is called the base period or the base of the crop.
Crop period is slightly more than the base period, but for all practical purposes, they are taken as one and the same thing, and generally expressed in days. - Delta of a Crop (Δ)
Each crop requires a certain amount of water after a certain fixed interval of time, throughout its period of growth.
The total quantity of water required by the crop for its full growth may be expressed in hectare metre (ha.m) or simply as depth to which water would stand on the irrigated area if the total quantity supplied were to stand above the surface without percolation or evaporation. This total depth of water (in cm) required by a crop to come to maturity is called its delta (Δ).
Explanation: The depth of water required every time, generally varies from 5 to 10 cm depending upon the type of the crop. If this depth of water is required five times during the base period, then the total water required by the crop for its full growth will be 5 multiplied by each time depth. The final figure will represent the total quantity of water required by the crop for its full-fledged nourishment.
Example 1: If rice requires about 10cm depth of water at an average interval of about 10 days, and the crop period for rice is 120 days, find out the delta for rice.
Solution: Water is required at an interval of 10 days for a period of 120 days. It evidently means that 12 no. of waterings are required, and each time, 10 cm depth of water is required. Therefore, the total depth of water required.
= 12 x 10 cm = 120 cm.
Hence Δ for rice = 120 cm.
Example 2: If wheat requires about 7.5 cm of water after every 28 days, and the base period for wheat is 140 days, find out the value of delta for wheat.
Solution: Assuming the base period to be representing the crop period, as per usual practise, we can easily infer that the water is required at an average interval of 28 days up to a total period of 140days.
This means that 5(140 / 28) no. of waterings are required 28days
The depth of water required each time = 7.5 cm.
Total depth of water required. In 140 days = 5 x 7.5 = 37.5 cm
Hence, Δfor wheat = 37.5 cm. - Delta for certain crops
The average values of deltas for certain crops are shown in the table. These values represent the total water requirement of the crops. The actual requirement of irrigation water may be less, depending upon the useful rainfall. Moreover, these values represent the values on the field, i.e. ‘delta on field’ which includes losses.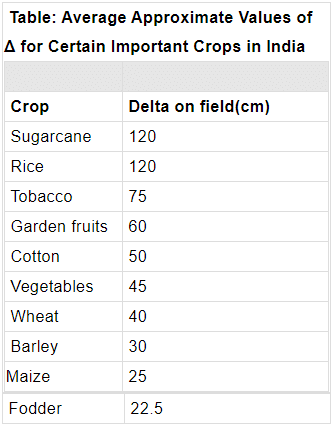
- Duty of Water (D)
The term duty means the "area of land" that can be irrigated with the unit volume of irrigation water. Quantitatively, duty is defined as the area of land expressed in hectares that can be irrigated with unit discharge, that is, 1 cumec flowing throughout the base period, expressed in days.
If water flowing at a rate of one cubic meter per second, runs continuously for B days and matures 200 hectares, then the duty of water for that particular crop will be defined as 200 hectares per cumec to the base of B days. Hence, duty is defined as the area irrigated per cumec of discharge running for base period B. The duty is generally represented by the letter D. - Relation between Duty(D) and Delta(Δ)
Let there be a crop of base period B days. Let one cumec of water be applied to this crop on the field for B days. Now, the volume of water applied to this crop during B days.
Volume of water applied to crop = V = (1 x60 x60 x24 xB) m3. = 86400 B (cubic metre)
By definition of duty (D), one cubic metre supplied for B days matures D hectares of land.
This quantity of water (V) matures D hectares of land or 104 D sq.m of area.
Total depth of water applied on this land = Volume / Area = 86,400 B / 104 D . 8.64B / D metres
By definition, this total depth of water is called delta (Δ).
Δ = 8.64B / D (metres)
Where
Δ is in meter, B is in days; and
D is duty in hectares/cumec.
During the passage of water from these irrigation channels, water is lost due to evaporation and percolation. These losses are called Transit losses or Transmission or Conveyance losses in channels.
Layout of Canal System
Duty of water for a crop is the number of hectares of land which the water can irrigate. Therefore, if the water requirement of the crop is more, less number of hectares of land it will irrigate. Hence, if water consumed is more, duty will be less. It, therefore, becomes clear that the duty of water at the head of the watercourse will be less than the because when water flows from the head of the watercourse and reaches the field, some water is lost as transit losses.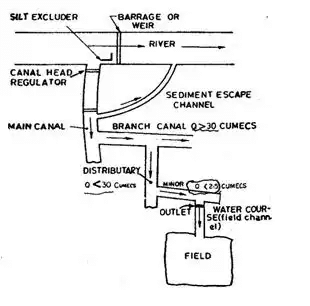
Applying the same reasoning, it can be established that duty of water at the head of a minor will be less than that at the head of the watercourse; duty at the head of a distributary will be less than that at the head of a minor, duty at the head of a branch canal will be less than that at the head of a minor, duty at the head of the main canal will be less that the duty at the head of a branch canal.
Duty of water, therefore, varies from one place to another and increases as we move downstream from the head of the main canal towards the head of the branches or watercourses. The duty at the head of the watercourse (i.e. at the outlet point is generally the endpoint of Irrigation Department.
Factors Affecting Duty of Water
- Climatic and season: As stated earlier, duty includes the water lost in evaporation and percolation. These losses will vary with the season. Hence, duty varies from season to season, and also from time to time in the same season. The figures for duties which we generally express are their average values considered over the entire crop period.
- Useful rainfall: If some of the rain, falling directly over the irrigated land, is useful for the growth of the crop, then so much less irrigation water will be required to mature the crop. More the useful rainfall, less will be the requirement of irrigation water, and hence more will be the duty of irrigation water.
- Type of soil: If the permeability of the soil under the irrigated crop is high, the water lost due to percolation will be more and hence, the duty will be less. Therefore, for sandy soils, where the permeability is more, the duty of water is less.
- The efficiency of cultivation method: If the cultivation method (including tillage and irrigation) is faulty and less efficient, resulting in the wastage of water, the duty of water will naturally be less. If the irrigation water is used economically, then the duty of water will improve, as the same quantity of water would be able to irrigate more area. Cultivators should, therefore, be trained and educated properly to use irrigation water economically.
Importance of duty
It helps us in designing an efficient canal irrigation system. Knowing the total available water at the head of the main canal, and the overall duty for all the crops required to be irrigated in different seasons of the year, the area which can be irrigated can be worked out. Inversely, if we know the corps area required to be irrigated and their duties, we can work out the discharge required for designing the channel.
Irrigation Efficiencies
Efficiency is the ratio of the water output to the water input and is usually expressed as the percentage. Input minus output is nothing but losses, and hence, if losses are more, the output is es and, therefore, efficiency is less. Hence, efficiency is inversely proportional to the losses. Water is lost in irrigation during various processes and, therefore, there are different kinds of irrigation efficiencies, as given below.
- Efficiency of water-conveyance (ηc): It is a ratio of the water delivered into the fields from the outlet point of the channel to the water pumped into the channel at the starting point. It may be represented by ηc. It takes the conveyance or transit losses into account.
- Efficiency of water application (ηa): It is the ratio of the quantity of water stored into the root zone of the crops to the quantity of water actually delivered into the field. it may be represented by ηa. It may also be termed as farm efficiency, as it takes into account the water is lost on the farm.
- Efficiency of water storage (ηs): It is the ratio of the water stored in the root zone during irrigation to the water needed in the root zone prior to irrigation (i.e., field capacity –existing moisture content). It may be represented by ηs.
- Efficiency of water use (ηu): It is the ratio of the water beneficially used, including leaching water, to the quantity of water delivered. It may be represented by ηu.
Example 3: Once cumec of water is pumped into a farm distribution system. 0.8 cumec is delivered to a turnout, 0.9 kilometres from the well. Compute the conveyance efficiency.
Solution: By definition
ηc = Output / Input x 100 = 0.8 / 1.0.100 = 80%
Example 4: 10 cumecs of water is delivered to a 32-hectare field, for 4 hours. Soil probing after the indicated that 0.3 metres of water has been stored in the root zone. Compute the water application efficiency.
Solution: Volume of water supplied by 10 cumecs of water applied for 4 hours =(10 x 4 x 60 x 60)m3 = 1,44,000 m3
= 14.4 x 104 m3 = 14.4m x 104m2 = 14. 4ha.m.
Depth of water applied =
volume/area = 1,44,000 / 32,0,000 = 144 / 320 = .45
Input = 14.4 ha.m
Output = 32 hectares land is storing water upto 0.3 m depth,
Output = 32 x 0.3 ha.m = 9.6 ha.m
Water application efficiency (ηa) = Output/ Input x 100 = ( 9.6 / 14.4) x 100 = 67% - Uniformity coefficient or Water distribution efficiency: The effectiveness of irrigation may also be measured by its water distribution efficiency (ηd ), which is defined below:
ηd = (1 - d / D) x 100
Where ηd = Water distribution efficiency
D = Mean depth of water stored during irrigation.
d = Average of the absolute values of deviations from the mean.
The water distribution efficiency represents the extent to which the water has penetrated to a uniform depth, throughout the field. When the water has penetrated uniformly throughout the field, the deviation from the mean depth is zero and water distribution efficiency is 1.0.
Example 5: A stream of 130 litres per second was diverted from a canal and 100 litres per second were delivered to the field. An area of 1.6 hectares was irrigated in 8 hours. The effective depth of the root zone was 1.7 m. The runoff loss in the field was 420 cu. M. The depth of water penetration varied linearly from 1.7 m at the head end of the field to1.1 m at the tail end. Available moisture-holding capacity of the soil is 20 cm per metre depth of soil. It is required to determine the water conveyance efficiency, water application efficiency, water storage efficiency, and water distribution efficiency. Irrigation was started at a moisture extraction level of 50% of the available moisture.
Solution: (i) Water conveyance efficiency (ηc)
=( Water delivered to the fields/ Water supplied into the canal at the head) x 100
= 100 / 130 x 100 =77%
(ii) Water application efficiency (ηa)
Water stored in the root zone during irrigation / Water delivered to the field x 100
Water supplied to field during 8 hours @ 100 litres per second
= 100 x 8 x 60 x 60 litres = 2880 cu. m.
Runoff loss in the field = 420 cu. M.
the water stored in the root zone = 2880 – 420 = 2460 cu. m.
(iii) Water application efficiency (ηa)
= 2460 / 100 = 85.4% Ans. 2880
(iv) Water storage efficiency (ηs) = (Water stored in the root zone during irrigation /
Water needed in the root zone prior to irrigation) x 100
Moisture holding capacity of soil
= 20 cm per m depth x 1.7 m depth of root zone = 34 cm
Moisture already available in the root zone at the time of start of irrigation = 50 / 100 x 34 = 17cm.
Additional water required in the root zone
= 34 – 17 = 17 cm.
= 2720 cu. m.
But actual water stored in root zone = 2460 cu. m.
Water storage efficiency (ηs) =2460 / 2720 x 100 90% (say)
(v) Water distribution efficiency
Where D = mean depth of water stored in the root zone
D = ( 1.7 + 1.1 ) / 2 = 1.4m
d is computed as below:
Deviation from the mean at upper end (absolute value) = |1.7 - 1.4| = 0.3
Deviation from the mean at lower end = | 1.1 - 1.4 | =0.3
d = Average of the absolute values of deviations from mean = 0.4 + 0.3 / 2 = 0.35
Using equations, we have,
ηd = 75 or 75% Ans. - Consumptive Use or Evapotranspiration (Cu): Consumptive use for a particular crop may be defined as the total amount of water used by the plant in transpiration (building of plant tissues, etc.) and evaporation from adjacent soils or from plant leaves, in any specified time. The values of consumptive use (Cu) may be different for different crops, and may be different for the same crop at different times and places.
In fact, the consumptive use for a given crop at a given place may vary throughout the day, throughout the month and throughout the crop period. Values of daily consumptive use or monthly consumptive use, are generally determined for a given crop and at a given place. Values of monthly consumptive use over the entire crop period are then used to determine the irrigation requirement of the crop.
Effective Rainfall (Re)
Precipitation falling during the growing period of a crop that is available to meet the evapotranspiration needs of the crop is called effective rainfall. It does not include precipitation lost through deep percolation below the root zone or the water lost as surface runoff.
Consumptive Irrigation Requirement (CIR)
It is the amount of Irrigation water required in order to meet the evapotranspiration needs of the crop during its full growth. It is, therefore, nothing but the consumptive use itself, but exclusive of effective precipitation, stored soil moisture, or ground water. When the last two are ignored, then we can write
CIR = Cu - Re
Net Irrigation Requirement (NIR)
It is the amount of irrigation water required in order to meet the evapotranspiration need of the crop as well as other needs such as leaching. Therefore, N.I.R. = Cu – Re + Water lost as percolation in satisfying other needs such as leaching.
Consumptive use or evapotranspiration depends upon all those factors on which evaporation and transpiration depend; such as temperature, sunlight, humidity, wind movement, etc.
Estimation of Consumptive Use
Although various methods have been developed in order to estimate evapotranspiration (consumptive use) value of a crop in an area, but the most simple and commonly used methods are:
- Blaney –Criddle Equation, and
- Hargreaves class A pan evaporation method
- Blaney-Criddle Formula:
It sates that the monthly consumptive use is given by
Cu = K.(P / 40 [1.8t + 32])
where, Cu = Monthly consumptive use in cm.
k = Crop factor, determined by experiments for each crop, under the environmental conditions of the particular area.
t = Mean monthly temperature in oC
p = Monthly pet cent of annual day light hours that occur during the period.
If p / 40 [1.8t + 32]is represented by f, we get
Cu = k.f
Example: The monthly consumptive use values for Paddy are tabulated in Table. Determine the total consumptive use. What is the average monthly consumptive use and peak monthly consumptive use?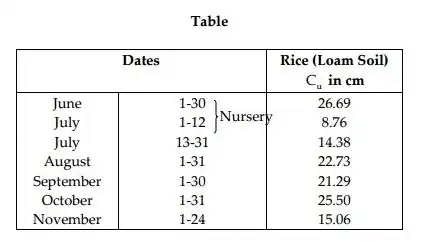
Solution: The summation of consumptive uses
= 29.69 + 8.76 + 14.38 + 22.73 + 21.29 + 25.50 + 15.06 = 137.41 cm
Hence, total consumptive use for paddy = 137.41 cm.
Average daily consumptive use =
137.4 / Period of growth in days =
= 137.41 / 31 + 31 + 31 + 30 + 31 + 24
= 137.41 / 177 = 0.77 cm. = 0.77 x 30=23.1 mm.
Average monthly consumptive use = 0.77 × 30 = 23.1 mm.
Peak monthly consumptive use = 26.69 cm. (Highest value is given)
|
7 videos|47 docs|31 tests
|
FAQs on Water Requirements of Crops - Irrigation Engineering - Civil Engineering (CE)
| 1. What factors determine the water requirements of crops? |  |
| 2. How can I determine the water requirements of specific crops? |  |
| 3. What are some efficient irrigation methods to meet crop water requirements? |  |
| 4. How can farmers manage water resources effectively for crop irrigation? |  |
| 5. How can climate change impact the water requirements of crops? |  |





















