Fundamental Theorem of Calculus | Mathematics (Maths) Class 12 - JEE PDF Download
Fundamental Theorem of Calculus
The fundamental theorem of calculus is a theorem that links the concept of integrating a function with that of differentiating a function. The fundamental theorem of calculus justifies the procedure by computing the difference between the antiderivative at the upper and lower limits of the integration process. In this article, let us discuss the first, and the second fundamental theorem of calculus, and evaluating the definite integral using the theorems in detail.
Area Function
Let’s consider a function f in x that is defined in the interval [a, b]. The integral of f(x) between the points a and b i.e.  is the area that is bounded by the curve y = f(x) and the lines x = a, x =b and x – axis
is the area that is bounded by the curve y = f(x) and the lines x = a, x =b and x – axis 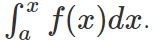 depicts the area of the region shaded in brown where x is a point lying in the interval [a, b]. Assuming that the values taken by this function are non- negative, the following graph depicts f in x.
depicts the area of the region shaded in brown where x is a point lying in the interval [a, b]. Assuming that the values taken by this function are non- negative, the following graph depicts f in x.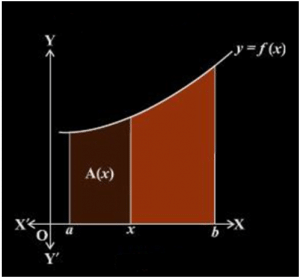
A(x) is known as the area function which is given as;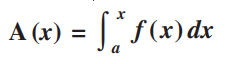
Depending upon this, the fundamental theorem of Calculus can be defined as two theorems as stated below:
First Fundamental Theorem of Integral Calculus (Part 1)
The first part of the calculus theorem is sometimes called the first fundamental theorem of calculus. It affirms that one of the antiderivatives (may also be called indefinite integral) say F, of some function f, may be obtained as integral of f with a variable bound of integration. From this, we can say that there can be antiderivatives for a continuous function.
Statement: Let f be a continuous function on the closed interval [a, b] and let A(x) be the area function. Then A′(x) = f(x), for all x ∈ [a, b].
Or
Let f be a continuous real-valued function defined on a closed interval [a, b]. Let F be the function defined, for all x in [a, b], by: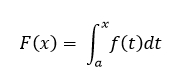
Then F is uniformly continuous on [a, b] and differentiable on the open interval (a, b), and F'(x) = f(x) ∀ x ∈(a, b)
Here, the F'(x) is a derivative function of F(x).
Second Fundamental Theorem of Integral Calculus (Part 2)
The second fundamental theorem of calculus states that, if the function “f” is continuous on the closed interval [a, b], and F is an indefinite integral of a function “f” on [a, b], then the second fundamental theorem of calculus is defined as:
F(b)- F(a) = ∫ab f(x) dx
Here R.H.S. of the equation indicates the integral of f(x) with respect to x.
f(x) is the integrand.
dx is the integrating agent.
‘a’ indicates the upper limit of the integral and ‘b’ indicates a lower limit of the integral.
The function of a definite integral has a unique value. The definite integral of a function can be described as a limit of a sum. If there is an antiderivative F of the function in the interval [a, b], then the definite integral of the function is the difference between the values of F, i.e., F(b) – F(a).
Remarks on the Second Fundamental Theorem of Calculus
- The second part of the fundamental theorem of calculus tells us that ∫ab f(x) dx = (value of the antiderivative F of “f” at the upper limit b) – (the same antiderivative value at the lower limit a).
- This theorem is very beneficial because it provides us with a method of estimating the definite integral more quickly, without determining the sum’s limit.
- In estimating a definite integral, the essential operation is finding a function whose derivative is equal to the integrand. However, this process will reinforce the relationship between differentiation and integration.
- In the expression ∫ab f(x) dx, the function f(x) or say “f” should be well defined and continuous in the interval [a, b].
How to Calculate Definite Integral?
Here are the steps for calculating ∫ba f(x)dx
- Determine the indefinite integral of f(x) as F(x). It must be noticed that arbitrary constant is not considered while calculating definite integrals since it cancels out itself, i.e.,

- Calculate F(b) – F(a) which gives us the value of the definite integral of f in x lying between the closed interval [a, b].
Examples
Q.1: Evaluate the integral: ∫23 y2dy
Solution: Let I = ∫23 y2dy
As we know,
∫y2dy = y3/3 = F(y)
Therefore, by second fundamental calculus theorem, we know;
I = F(3) – F(2) = 27/3 – 8/3 = 19/3
Q.2: Evaluate the integral: ∫12[ydy/(y+1)(y+2)]
Solution: By partial fraction we can factorise the term under integral.
y/[(y+1)(y+2)] = [-1/(y+1)]+[2/(y+2)] So,
∫y/[(y+1)(y+2)] = -log|y+1|+2log|x+2| = F(y)
Hence, by fundamental theorem of calculus part 2, we get;
I = F(2)-F(1) = [– log 3 + 2 log 4] – [– log 2 + 2 log 3] I = – 3 log 3 + log 2 + 2 log 4
I = log(32/27)
Practice Problems
Get more questions here for practice to understand the concept quickly.
Evaluate using the fundamental theorem of calculus: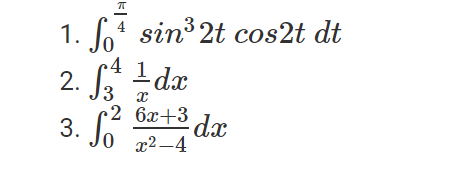
Frequently Asked Questions
What is the first fundamental theorem of calculus?
First fundamental theorem of integral calculus states that “Let f be a continuous function on the closed interval [a, b] and let A (x) be the area function. Then A′(x) = f (x), for all x ∈ [a, b]”.
How many fundamental theorems of calculus are there?
Two basic fundamental theorems have been given in calculus for calculating the area using definite integrals:
First fundamental theorem of integral calculus
Second fundamental theorem of integral calculus
What are the 4 concepts of calculus?
The 4 concepts of calculus are:
Limits and functions
Derivatives
Integrals
Infinite series
What is the second fundamental theorem of calculus?
Second fundamental theorem of integral calculus states that “Let f be a continuous function defined on the closed interval [a, b] and F be an antiderivative of f. Then ∫_{a}^{b} f(x) dx = [F(x)]_{a}^{b} = F(b) – F(a).
Who first proved the fundamental theorem of calculus?
The first published statement and proof of a basic form of the fundamental theorem, strongly geometric, was given by James Gregory. Isaac Barrow proved a more generalized version of the theorem, while his student Isaac Newton finished the development of the enclosing mathematical theory.
|
204 videos|290 docs|139 tests
|