Force Methods/Flexibility Method | Structural Analysis - Civil Engineering (CE) PDF Download
Introduction
- For determinate structures, the force method allows us to find internal forces (using equilibrium i.e. based on Statics) irrespective of the material information. Material (stress-strain) relationships are needed only to calculate deflections.
- However, for indeterminate structures , Statics (equilibrium) alone is not sufficient to conduct structural analysis. Compatibility and material information are essential.
- The flexibility method is based upon the solution of "equilibrium equations and compatibility equations". There will always be as many compatibility equations as redundants. It is called the flexibility method because flexibilities appear in the equations of compatibility. Another name for the method is the force method because forces are the unknown quantities in equations of compatibility.
The force method is used to calculate the response of statically indeterminate structures to loads and/or imposed deformations. The method is based on transforming a given structure into a statically determinate primary system and calculating the magnitude of statically redundant forces required to restore the geometric boundary conditions of the original structure.
The basic steps in the force method are as follows:
- Determine the degree of static indeterminacy, n of the structure.
- Transform the structure into a statically determinate system by releasing a number of static constraints equal to the degree of static indeterminacy, n. This is accomplished by releasing external support conditions or by creating internal hinges. The system thus formed is called the basic determinate structure.
- For a given released constraint j, introduce an unknown redundant force Rf corresponding to the type and direction of the released constraint.
- Apply the given loading or imposed deformation to the basic determinate structure. Use suitable method (given in Chapter 4) to calculate displacements at each of the released constraints in the basic determinate structure.
- Solve for redundant forces Rf ( j =1 to n ) by imposing the compatibility conditions of the original structure. These conditions transform the basic determinate structure back to the original structure by finding the combination of redundant forces that make displacement at each of the released constraints equal to zero.

Types of Force Method/Flexibility Method/Compatibility Methods
- Virtual work/Unit load Method
- Method of consistent deformation
- Three-moment theorem
- Castigliano's theorem of minimium strain energy
- Maxwell-Mohr's equation
- Column Analogy Method
Strain Energy Method
- Strain energy stored due to axial load
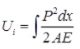
where, P = Axial load
dx = Elemental length
AE = Axial rigidity - Strain energy stored due to bending
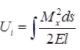
where, MX = Bending moment at section x-x
ds = Elemental length
El = Flexural rigidity
or E = Modulus of elasticity
l = Moment of inertia - Strain energy stored due to shear
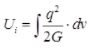
where, q = Shear stress
G = Modulus of rigidity
dv = Elemental volume - Strain energy stored due to shear force
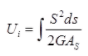
where, AS = Area of shear
S = Shear force
G = Modulus of rigidity
ds = Elemental length - Strain energy stored due to torsion
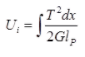
where, T = Torque acting on circular bar
dx = Elemental length
G = Modulus of rigidity
lP = Polar moment of inertia - Strain energy stored in terms of maximum shear stress
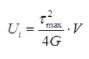
where, Maximum shear stress at the surface of rod under twisting.
G = Modulus of rigidity
V = Volume - Strain energy stored in hollow circular shaft is,
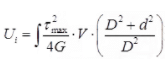
Where, D = External dia of hollow circular shafts
d = Internal dia of hollow circular shaft
τmax = Maximum shear stress - Castigliano's first Theorem
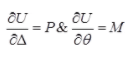
where, U = Total strain energy
Δ = Displacement in the direction of force P.
θ = Rotation in the direction of moment M. - Castiglianos Second Theorem
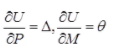
Betti's Law
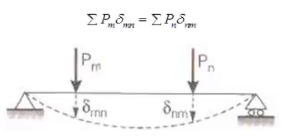
where, Pm = Load applied in the direction m.
Pn = Load applied in the direction n.
δmn = Deflection in the direction 'm' due to load applied in the direction 'n'.
δnm = Deflection in the direction 'n' due to load applied in the direction 'm'.
Maxwells Reciprocal Theorem
δ21 = δ12
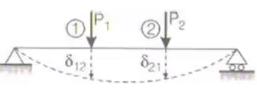
where, δ21 = deflection in the direction (2) due to applied load in the direction (1).
δ12 = Deflection in the direction (1) due to applied load in the direction (2).
Some Solved Examples
Example 1: Analyze the continuous beam shown below using the force method. Also, draw the bending moment diagram. EI is constant for entire beam.
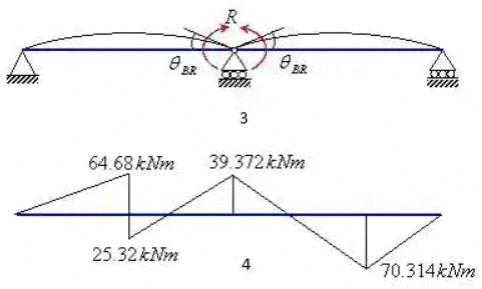
 Solution: The degree of static indeterminacy = 3–2 =1. The moment at B is taken as redundant R and the basic determinate structure will be then two simply supported beams as shown below
Solution: The degree of static indeterminacy = 3–2 =1. The moment at B is taken as redundant R and the basic determinate structure will be then two simply supported beams as shown below
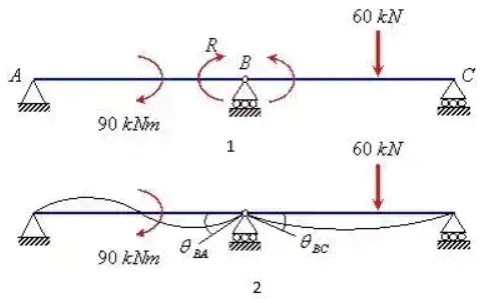
Rotation of point B due to applied loads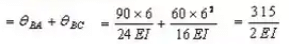
Rotation of point B due to R
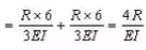
Equating the rotation of point 8 due to applied loads and R i.e.
4R/El = 315/2E1
or R = 39.375 kNm
The reaction at A is given by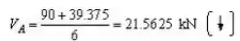
The vertical reaction at C Is given by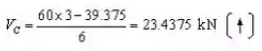
The vertical reaction at B is
VB = 60 + 21.5625 - 23.4375 = 58.125 kN
The bending moment diagram of the beam is shown in Figure 4.
Example 2: Find the force in various members of the pin-jointed frame shown in figure below. AE is constant for all members.
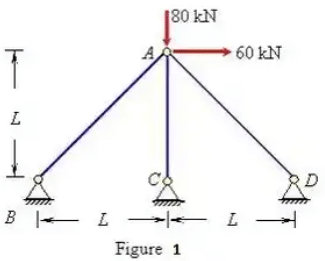
 Basic determinate structure under the applied load and unknown R
Basic determinate structure under the applied load and unknown R
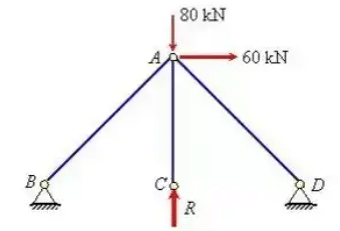
Solution: The static indeterminacy of the pin-jointed frame = 1. The vertical reaction at C is taken as unknown force R . The computation of deflection of point C due to applied loading and R are shown in Tables 2 and 3, respectively.
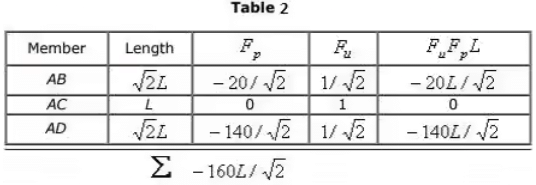
The vertical displacement of joint C due to applied loading = - 160L/√2AE (↓)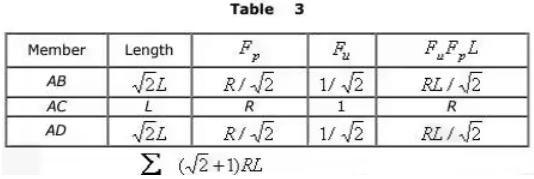
The vertical displacement of Joint C due to R = 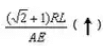
Adding the displacement of point C due to applied loading and R and equating It to zero i.e.
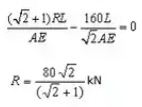
The force in various members of the frame are as follows

Example 3: Find the expression for the prop reaction in the propped cantilever beam shown in the figure below.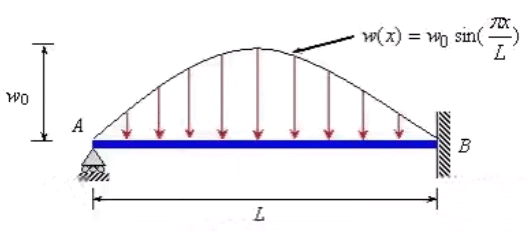
Solution: Let reaction at support A be R . According to the Castigliano's theorem
∂U/∂R = 0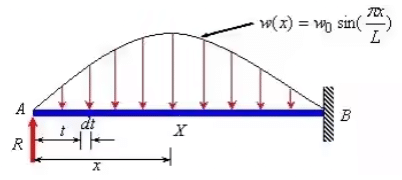
The bending moment at any point X at a distance x from A is given by
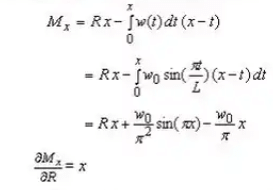
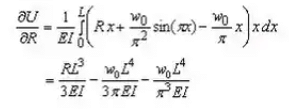
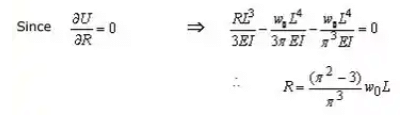
Example 4: Analyze the continuous beam shown in figure shown beolw by the three moment equation. Draw the shear force and bending moment diagram.
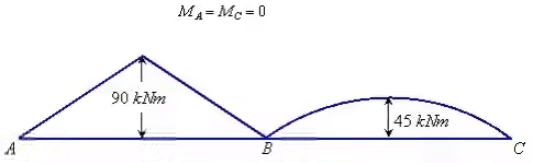
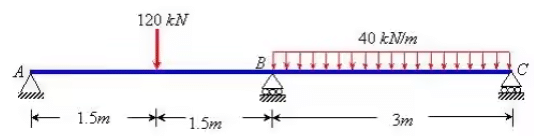 Solution: The simply supported bending moment diagram on AB and AC are shown below. Since supports A and C are simply supported
Solution: The simply supported bending moment diagram on AB and AC are shown below. Since supports A and C are simply supported
Applying the three moment equation to span AEI and BC (Δ1 = Δ2 = Δ3 = 0)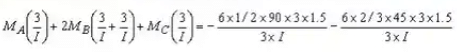
or Mb = -56.25 kN.m
The reactions at support A, B and C are given as

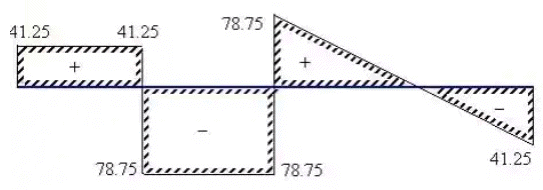
VB = 120 + 40 x 3 - 41.25 - 41.25 =157.5 kN
The bending moment and shear force diagram are shown below in figure.
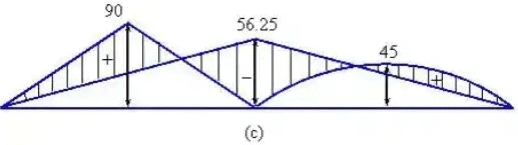
|
32 videos|154 docs|31 tests
|
FAQs on Force Methods/Flexibility Method - Structural Analysis - Civil Engineering (CE)
| 1. What is the Force Method in structural analysis? |  |
| 2. What is the Flexibility Method in structural analysis? |  |
| 3. What is GATE in the context of structural analysis? |  |
| 4. How is the Force Method different from the Flexibility Method? |  |
| 5. What are the advantages of using the Force Method and the Flexibility Method in structural analysis? |  |
















