Representations of Matrices and Graphs in Relations | Engineering Mathematics - Engineering Mathematics PDF Download
Combining Relation
Suppose R is a relation from set A to B and S is a relation from set B to C, the combination of both the relations is the relation which consists of ordered pairs (a, c) where a Є A and c Є C and there exist an element b Є B for which (a, b) Є R and (b, c) Є S. This is represented as RoS.
Inverse Relation
A relation R is defined as (a, b) Є R from set A to set B, then the inverse relation is defined as (b, a) Є R from set B to set A. Inverse Relation is represented as R-1
R-1 = {(b, a) | (a, b) Є R}.
Complementary Relation
Let R be a relation from set A to B, then the complementary Relation is defined as- {(a, b)} where (a, b) is not Є R.
Representation of Relations
Relations can be represented as- Matrices and Directed graphs.
Relation as Matrices:
A relation R is defined as from set A to set B, then the matrix representation of relation is MR = [mij] where
mij = { 1, if (a, b) Є R
0, if (a, b) Є R }
Properties- A relation R is reflexive if the matrix diagonal elements are 1.

- A relation R is irreflexive if the matrix diagonal elements are 0.
- A relation R is symmetric if the transpose of relation matrix is equal to its original relation matrix. i.e. MR = (MR)T.

- A relation R is antisymmetric if either mij = 0 or mji = 0 when i≠j.
- A relation follows join property i.e. the join of matrix M1 and M2 is M1 V M2 which is represented as R1 U R2 in terms of relation.
- A relation follows meet property i.r. the meet of matrix M1 and M2 is M1 ^ M2 which is represented as R1 Λ R2 in terms of relation.
Relations as Directed graphs
A directed graph consists of nodes or vertices connected by directed edges or arcs. Let R is relation from set A to set B defined as (a,b) Є R, then in directed graph-it is represented as edge(an arrow from a to b) between (a,b).
Properties- A relation R is reflexive if there is loop at every node of directed graph.
- A relation R is irreflexive if there is no loop at any node of directed graphs.
- A relation R is symmetric if for every edge between distinct nodes, an edge is always present in opposite direction.
- A relation R is asymmetric if there are never two edges in opposite direction between distinct nodes.
- A relation R is transitive if there is an edge from a to b and b to c, then there is always an edge from a to c.
Example:
The directed graph of relation R = {(a, a), (a, b), (b, b), (b, c), (c, c), (c, b), (c, a)} is represented as
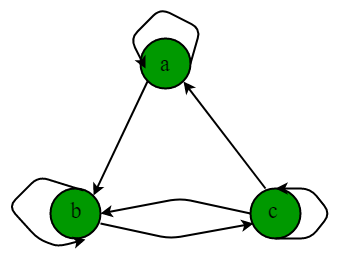
Since, there is loop at every node, it is reflexive but it is neither symmetric nor antisymmetric as there is an edge from a to b but no opposite edge from b to a and also directed edge from b to c in both directions. R is not transitive as there is an edge from a to b and b to c but no edge from a to c.
|
65 videos|129 docs|94 tests
|
FAQs on Representations of Matrices and Graphs in Relations - Engineering Mathematics - Engineering Mathematics
| 1. What is a matrix representation of a relation? |  |
| 2. How do you represent a directed graph as an adjacency matrix? |  |
| 3. Can a matrix representation of a relation be used to find the transitive closure of a directed graph? |  |
| 4. How can matrix representations of relations be used in data analysis and machine learning? |  |
| 5. What are the advantages of using a matrix representation for graphs and relations? |  |






















