Adjoint and Inverse of a Matrix | Mathematics (Maths) for JEE Main & Advanced PDF Download
The adjoint of a matrix (also called the adjugate of a matrix) is defined as the transpose of the cofactor matrix of that particular matrix. For a matrix A, the adjoint is denoted as adj (A). On the other hand, the inverse of a matrix A is that matrix which when multiplied by the matrix A give an identity matrix. The inverse of a Matrix A is denoted by A-1.
Adjoint of a Matrix
Let the determinant of a square matrix A be |A|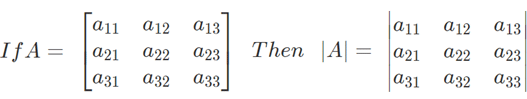
The matrix formed by the cofactors of the elements is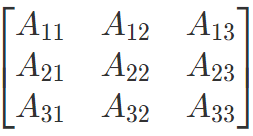
Where 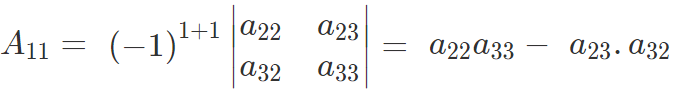
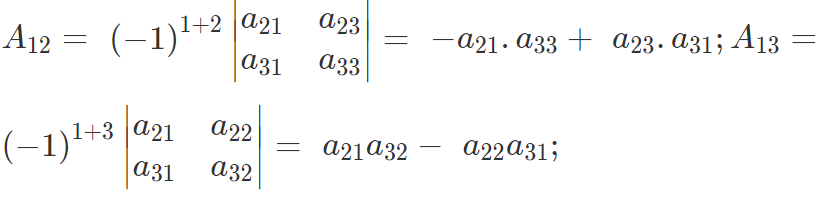
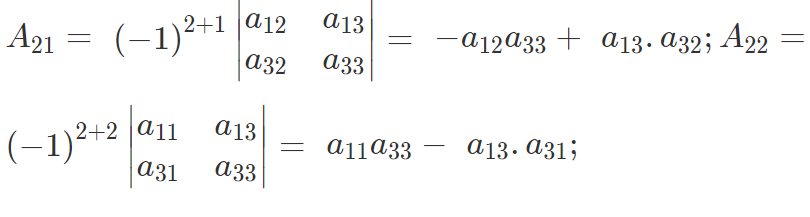
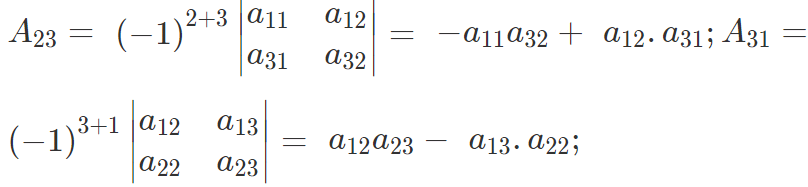
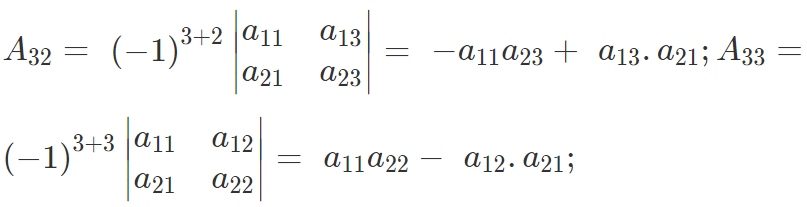
Then the transpose of the matrix of co-factors is called the adjoint of the matrix A and is written as adj A.
The product of a matrix A and its adjoint is equal to unit matrix multiplied by the determinant A.
Let A be a square matrix, then (Adjoint A). A = A. (Adjoint A) = | A |. I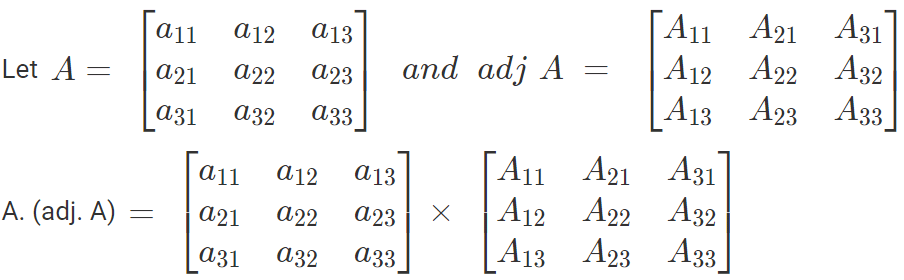
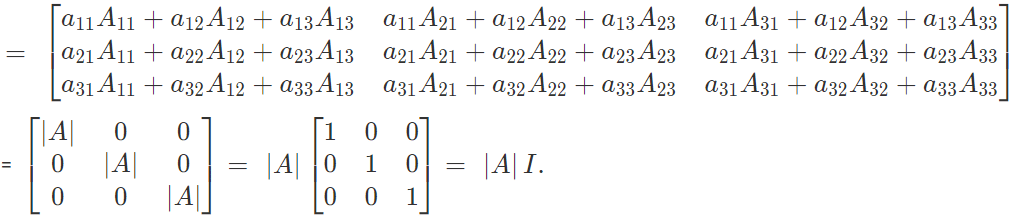
Example Problems on How to Find the Adjoint of a Matrix
Example 1: If AT = – A then the elements on the diagonal of the matrix are equal to
(a) 1
(b) -1
(c) 0
(d) none of these
Solution: (c) AT = -A; A is skew-symmetric matrix; diagonal elements of A are zeros.
so option (c) is the answer.
Example 2: If A and B are two skew-symmetric matrices of order n, then,
(a) AB is a skew-symmetric matrix
(b) AB is a symmetric matrix
(c) AB is a symmetric matrix if A and B commute
(d) None of these
Solution: (c) We are given A’ = -A and B’ = -B;
Now, (AB)’ = B’A’ = (-B) (-A) = BA = AB, if A and B commute.
Example 3: Let A and B be two matrices such that AB’ + BA’ = 0. If A is skew symmetric, then BA
(a) Symmetric
(b) Skew symmetric
(c) Invertible
(d) None of these
Solution: (c) we have, (BA)’ = A’B’ = -AB’ [ A is skew symmetric]; = BA’ = B(-A) = -BA
BA is skew symmetric.
Example 4: Let A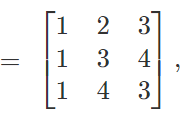
then adj A is given by –
Solution: Co-factors of the elements of any matrix are obtained by eliminating all the elements of the same row and column and calculating the determinant of the remaining elements.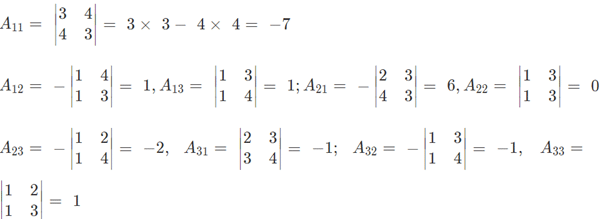
adj A = transpose of cofactor matrix.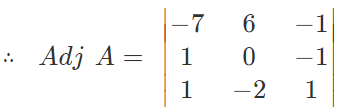
Example 5: Which of the following statements are false –
(a) If | A | = 0, then | adj A | = 0;
(b) Adjoint of a diagonal matrix of order 3 × 3 is a diagonal matrix;
(c) Product of two upper triangular matrices is an upper triangular matrix;
(d) adj (AB) = adj (A) adj (B);
Solution: (d) We have, adj (AB) = adj (B) adj (A) and not adj (AB) = adj (A) adj (B)
Inverse of a Matrix
If A and B are two square matrices of the same order, such that AB = BA = I (I = unit matrix)
Then B is called the inverse of A, i.e. B = A–1 and A is the inverse of B. Condition for a square matrix A to possess an inverse is that the matrix A is non-singular, i.e., | A | ≠ 0. If A is a square matrix and B is its inverse then AB = I. Taking determinant of both sides | AB | = | I | or | A | | B | = I. From this relation it is clear that | A | ≠ 0, i.e. the matrix A is non-singular.
How to find the inverse of a matrix by using the adjoint matrix?
We know that,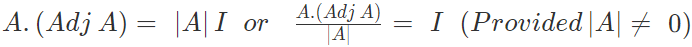
And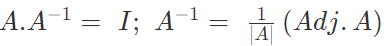
Properties of Inverse and Adjoint of a Matrix
- Property 1: For a square matrix A of order n, A adj(A) = adj(A) A = |A|I, where I is the identitiy matrix of order n.
- Property 2: A square matrix A is invertible if and only if A is a non-singular matrix.
Problems on Finding the Inverse of a Matrix
Illustration : Let A 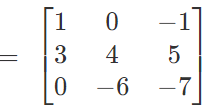
What is inverse of A?
Solution: By using the formula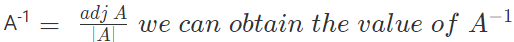
We have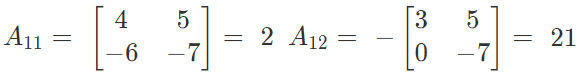
Similarly
A13 = -18 A31 =4, A32 = −8, A33 = 4, A21 = +6, A22 = −7, A23 = 6
cofactor matrix of A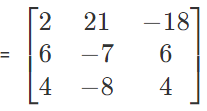
adj A = transpose of cofactor matrix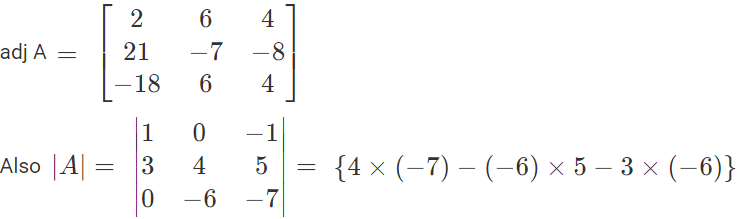
= -28 + 30 + 18
= 20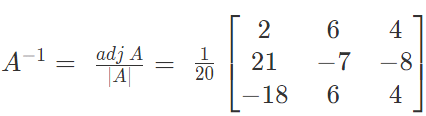
|
176 videos|582 docs|160 tests
|





















