Law of total probability | Engineering Mathematics - Engineering Mathematics PDF Download
Given n mutually exclusive events A1, A2, …Ak such that their probabilities sum is unity and their union is the event space E, then Ai ∩ Aj = NULL, for all i not equal to j, and
A1 U A2 U ... U Ak = E
Then Total Probability Theorem or Law of Total Probability is: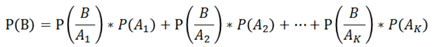
where B is an arbitrary event, and P(B/Ai) is the conditional probability of B assuming A already occured.
Proof:
Let A1, A2, …, Ak be disjoint events that form a partition of the sample space and assume that P(Ai) > 0, for i = 1, 2, 3….k.
such that:
A1 U A2 U A3 U ....U AK = E(Total)
Then, for any event B, we have,
B = B ∩ E
B = B ∩ (A1 U A2 U A3 U ....U AK)
As intersection and Union are Distributive. Therefore,
B = (B ∩ A1) U (B ∩ A2)U ... U(B ∩ AK)
Since all these partitions are disjoint. So, we have,
P(B ∩ A1) = P(B ∩ A1) U P(B ∩ A2)U ... U P(B ∩ AK)
That is, addition theorem of probabilities for union of disjoint events.
Using Conditional Probability
P(B / A) = P(B ∩ A) / P(A)
Or by the multiplication rule that,
P(B ∩ A) = P(B / A) x P(A)
Here events A and B are said to be independent events if P(B|A) = P(B), where P(A) not equal to Zero(0),
P(A ∩ B) = P(A) * P(B)
where P(B|A) is the conditional probability which gives the probability of occurrence of event B when event A has already occurred. Hence,
P(B ∩ Ai) = P(B | Ai).P(Ai) ; i = 1, 2, 3....k
Applying this rule above we get,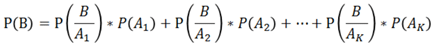
This is the law of total probability.
The law of total probability is also referred to as total probability theorem or law of alternatives.
Note: The law of total probability is used when you don’t know the probability of an event, but you know its occurrence under several disjoint scenarios and the probability of each scenario.
Application: It is used for evaluation of denominator in Bayes’ theorem.
Example: We draw two cards from a deck of shuffled cards with replacement. Find the probability of getting the second card a king.
Solution: Let,
A – represent the event of getting the first card a king.
B – represent the event that the first card is not a king.
E – represent the event that the second card is a king.
Then the probability that the second card will be a king or not will be represented by the law of total probability as:
P(E) = P(A)P(E | A) + P(B)P(E | B)
Where,
P(E) is the probability that second card is a king,
P(A) is the probability that the first card is a king,
P(E | A) is the probability that the second card is a king given that first card is a king,
P(B) is the probability that the first card is not a king,
P(E | B) is the probability that the second card is a king but the first card drawn is not a king.
According to question:
P(A) = 4 / 52
P(E | A) = 4 / 52
P(B) = 48 / 52
P(E | B) = 4 / 52
Therefore,
P(E)
= P(A)P(E | A) + P(B)P(E | B)
=(4 / 52) * (4 / 52) + (48 / 52) * (4 / 52)
= 0.0769230
|
65 videos|129 docs|94 tests
|
FAQs on Law of total probability - Engineering Mathematics - Engineering Mathematics
| 1. What is the law of total probability? |  |
| 2. How is the law of total probability applied in real-world scenarios? |  |
| 3. Can you provide an example to illustrate the law of total probability? |  |
| 4. Are there any limitations or assumptions associated with the law of total probability? |  |
| 5. How does the law of total probability relate to Bayes' theorem? |  |
















