Derivatives of a function in parametric form | Mathematics (Maths) for JEE Main & Advanced PDF Download

Derivatives of a function in parametric form: There are instances when rather than defining a function explicitly or implicitly we define it using a third variable. This representation when a function y(x)  is represented via a third variable which is known as the parameter is a parametric form. A relation between x and y can be expressible in the form x = f(t) and y = g(t) is a parametric form representation with parameter as t. Now we will concentrate on how to differentiate these functions using parametric differentiation. 

As we already know the chain rule of derivatives,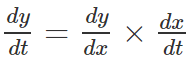

This chain rule can also be rewritten as,

Also, as mentioned earlier  y’ = g'(t) =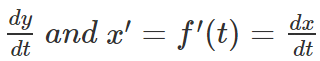

Thus we can say that,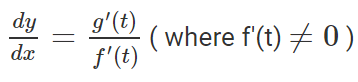

Rules for solving problems on derivatives of functions expressed in parametric form:
Step i) First of all we write the given functions x and y in terms of the parameter t.
Step ii) Using differentiation find out dy/dt and dx/dt.
Step iii) Then by using the formula used for solving functions in parametric form i.e.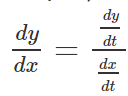

Step iv) Lastly substitute the values of dy/dt and dx/dt and simplify to obtain the result.

What is the Parametric equation?

When a group of quantities of one or more independent variables formed as functions, then they are called parametric equations. These are used to represent the coordinates of a point for any geometrical object like curve, surfaces, etc., where the equations of these objects are said to be a parametric representation of that particular object.
The general form of parametric equations are:
x = cos t
y = sin t
Here, (x, y) = (cos t, sin t) form a parametric form of the unit circle such that t is the parameter and (x, y) is the points on the unit circle.

Applications

Parametric functions are mainly used in the integration of different types of functions where the given function is in the complex form. In such cases, parameter t is used for substitution for some part of the given function. Other applications include graphs of various functions and equations that involve differentiation and so on. Now let us go through some examples to get a deeper insight for solving functions of the parametric form.

Parametric Differentiation Questions and Solutions

Example 1: Find the value of dy/dx for the following functions which are expressed in the parametric form.
i) x = sin t , y = t²
ii) x = 3/t³ ,y = 3t⁴ + 5
Solution:
i) Since this function is represented in parametric function format beforehand therefore we need to find out the value dy/dt and dx/dt.
Now, dy/dt = 2t
dx/dt = cost
Now with the help of chain rule we can write,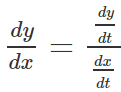

Now substituting the value of dy/dt and dx/dt into the above equation we can find the derivative of  w.r.t x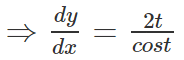

This is the required solution of the differentiation of the parametric equation.
ii) These functions are already expressed in terms of t. Therefore, to find dy/dx, evaluate dy/dt, and dx/dt separately.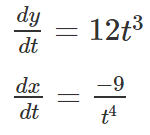

We know that,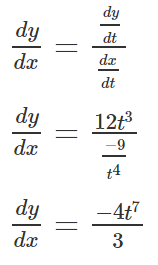

This is the required solution of the differentiation of the parametric equation.

Example 2: Find the value of dy/dt for y = e^sint and x=3t³
Solution: The given functions are parametric in nature.
And we know,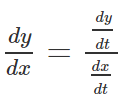


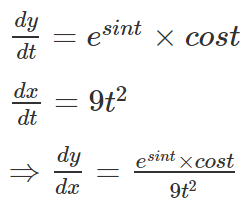
This is the required solution.