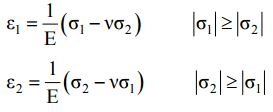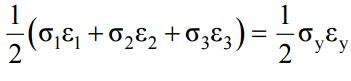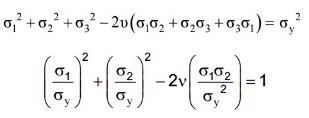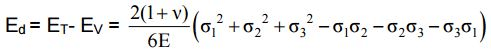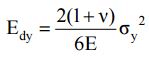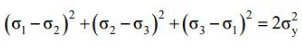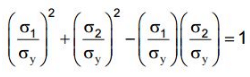Failure Theories | Strength of Materials (SOM) - Mechanical Engineering PDF Download
Theory of Failures
It is important to predict the failure mode in a machine component acted to a set of complex stress system so that suitable design method can be adapted for failure analysis.
- Theories of failure is a set of the theories especially designed for the complex stress system such as 3-D stresses.
- An element will be considered failed if it does not to perform its intended function.
There are basically two types of mechanical failure:
- Yielding: This is due to excessive inelastic deformation rendering the machine part unsuitable to perform its function. This mostly occurs in ductile materials.
- Fracture- in this case the component tears apart in two or more parts. This mostly occurs in brittle materials.
Failure: In order to design any machine element and find out the dimensions, failure, in different parts and different cross-sections are considered. A ductile material may fail by sudden fracture in different cases and this may occur if a material is subjected to:
(i) Cyclic loading
(ii) Long term static loading at elevated temperature
(iii) Impact loading
(iv) Work hardening
(v) Severe quenching
The Factor of Safety (FOS)
- The ratio of ultimate to allowable load or stress is known as factor of safety i.e. it is ratio of the material strength or failure stress to the allowable or working stress.
- The factor of safety must be always greater than unity. It is easier to refer to the ratio of stresses since this applies to material properties.
FOS = Failure Stress/Working or Allowable Stress
Ductile and Brittle Materials
- A ductile material deforms significantly before fracturing.
- Ductility is measured by % elongation at the fracture point.
- Materials with 5% or more elongation are considered ductile.
- The limiting strength of ductile materials is the stress at yield point.
- A brittle material yields very little before fracturing, the yield strength is approximately the same as the ultimate strength in tension.
- The ultimate strength in compression is much larger than the ultimate strength in tension.
- The limiting strength of brittle materials is the ultimate stress.
 |
Download the notes
Failure Theories
|
Download as PDF |
What is need for Failure Theory
- Static Failure theories predicting failures in members subjected to Uni-axial stress is both simple and straight-forward. While failure stresses for predicting failures in the components subjected to Bi-axial or Tri-axial stresses is much more complicated.
- There are various theories formulated and are as follows:
(i). Maximum Principal/Normal Stress Theory (Rankine’s Theory)
(ii). Maximum Shear Stress Theory (Guest’s Theory)
(iii). Maximum Principal /Normal Strain Theory (Saint’s Theory)
(iv). Maximum Strain Energy Theory (Haigh’s Theory)
(v). Maximum Distortion Energy Theory (Hencky & Von Mises Theory)
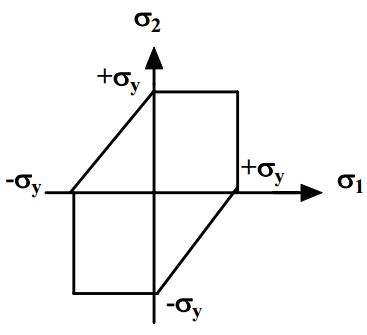
Maximum Principal Stress Theory (Rankine Theory):
- If one of the principal stresses σ1 (maximum principal stress), σ2 (minimum principal stress) or σ3 exceeds the yield stress, yielding would occur.
- In a two dimensional loading situation for a ductile material where tensile and compressive yield stress are nearly of same magnitude.
σ1 = ± σy
σ2 = ± σy
- Yielding occurs when the state of stress is at the boundary of the rectangle.
- At a point a, the stresses are still within the elastic limit but at b, σ1 reaches σy although σ2 is still less than σy.
- Yielding will then begin at point b
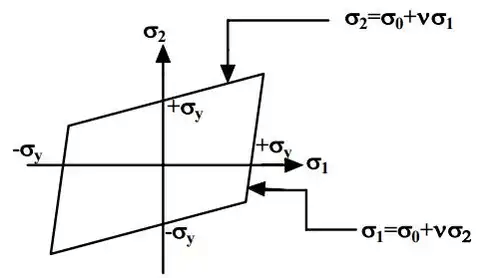
Maximum Principal Strain Theory (St. Venant’s theory):
- Yielding will occur when the maximum principal strain just exceeds the strain at the tensile yield point in either simple tension or compression.
- If ε1 and ε2 are maximum and minimum principal strains corresponding to σ1 and σ2, in the limiting case.

It implies:
Eε1 = σ1 - vσ2 = ± σ0
Eε2 = σ2 - vσ1 = ± σ0 - Boundary of a yield surface in Maximum Strain Energy Theory is given below

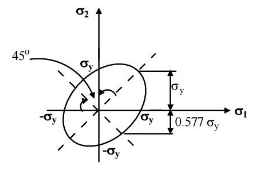
Maximum Shear Stress Theory (Tresca Theory):
- Yielding would occur when the maximum shear stress just exceeds the shear stress at the tensile yield point.
- At the tensile yield point σ2 = σ3 = 0 and thus maximum shear stress is σy/2.
- This gives us six conditions for a three-dimensional stress situation:
σ1 - σ2 = ± σy
σ2 - σ3 = ± σy
σ3 - σ1 = ± σy - Yield surface corresponding to maximum shear stress theory in biaxial stress situation is given below :

Maximum strain energy theory (Beltrami’s theory):
- Failure would occur when the total strain energy absorbed at a point per unit volume exceeds the strain energy absorbed per unit volume at the tensile yield point. This may be given:

- Substituting, ε1, ε2, ε3 and εy in terms of stresses we have

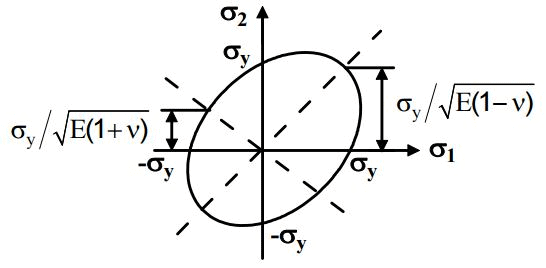
- Above equation results in Elliptical yield surface which can be viewed as:

Distortion energy theory (Von Mises yield criterion):
- Yielding would occur when total distortion energy absorbed per unit volume due to applied loads exceeds the distortion energy absorbed per unit volume at the tensile yield point. Total strain energy ET and strain energy for volume change EV can be given as:

- Substituting strains in terms of stresses the distortion energy can be given as:

- At the tensile yield point, σ1 = σy , σ2 = σ3 = 0 which gives,

- The failure criterion is thus obtained by equating Ed and Edy , which gives

- In a 2-D situation if σ3 = 0, so the equation reduces to,

- This is an equation of ellipse and yield equation is an ellipse.
- This theory is widely accepted for ductile material.

|
37 videos|41 docs|47 tests
|
FAQs on Failure Theories - Strength of Materials (SOM) - Mechanical Engineering
| 1. What are the main causes of mechanical failures in engineering? |  |
| 2. How does material defect contribute to mechanical failures? |  |
| 3. What is fatigue failure and how does it occur in mechanical systems? |  |
| 4. How does corrosion contribute to the failure of mechanical components? |  |
| 5. What role does poor maintenance play in mechanical failures? |  |