Merge Sort | Algorithms - Computer Science Engineering (CSE) PDF Download
Introduction
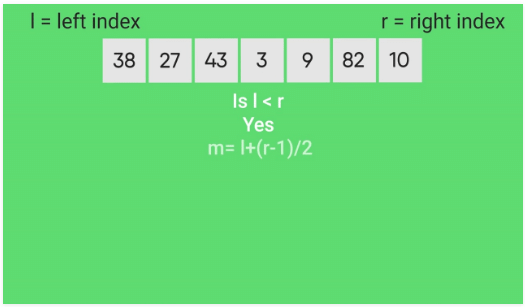
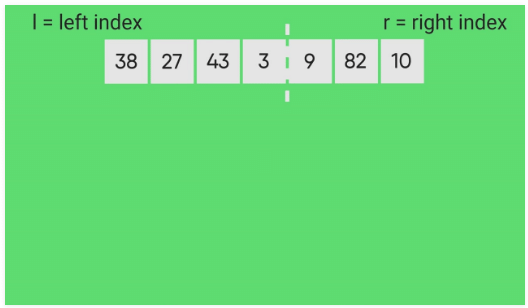
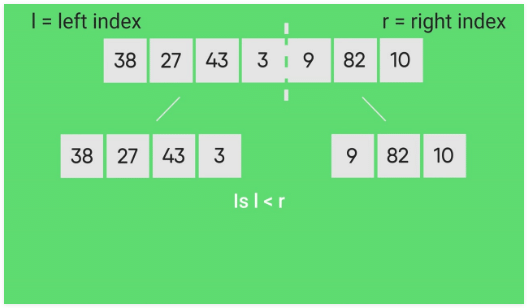
Like QuickSort, Merge Sort is a Divide and Conquer algorithm. It divides the input array into two halves, calls itself for the two halves, and then merges the two sorted halves. The merge() function is used for merging two halves. The merge(arr, l, m, r) is a key process that assumes that arr[l..m] and arr[m+1..r] are sorted and merges the two sorted sub-arrays into one. See the following C implementation for details.
MergeSort(arr[], l, r)
If r > l
- Find the middle point to divide the array into two halves:
middle m = l+ (r - l) / 2 - Call mergeSort for first half:
Call mergeSort(arr, l, m) - Call mergeSort for second half:
Call mergeSort(arr, m + 1, r) - Merge the two halves sorted in step 2 and 3:
Call merge(arr, l, m, r)
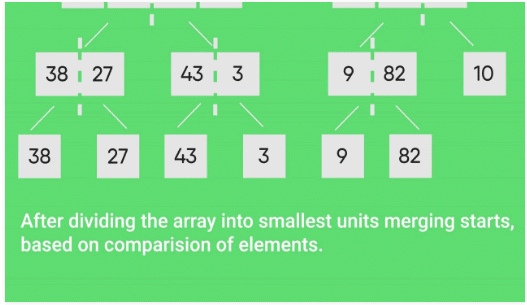
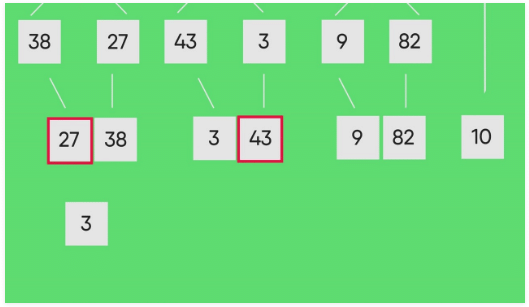
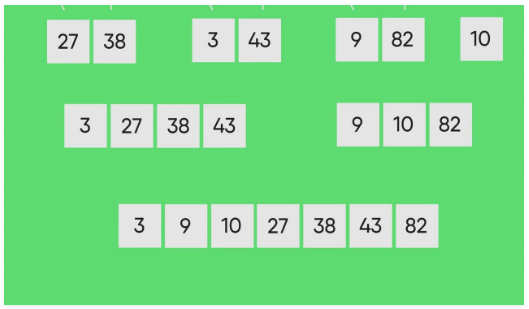
The following diagram shows the complete merge sort process for an example array {38, 27, 43, 3, 9, 82, 10}. If we take a closer look at the diagram, we can see that the array is recursively divided into two halves till the size becomes 1. Once the size becomes 1, the merge processes come into action and start merging arrays back till the complete array is merged.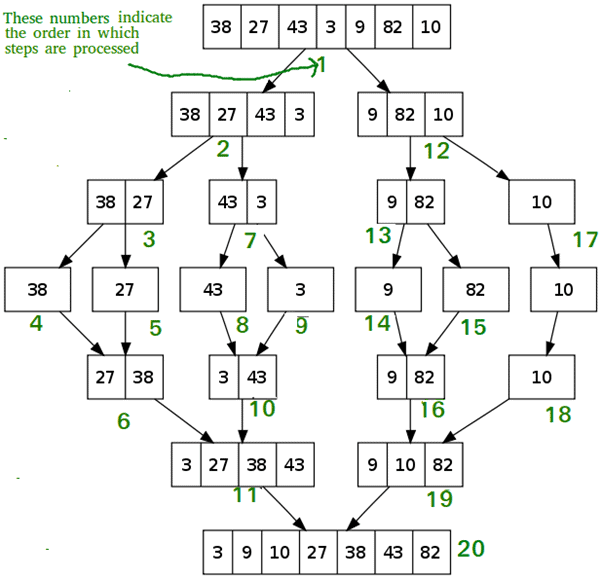
C++




C




Java




Python3


C#




Javascript




Output
Given array is
12 11 13 5 6 7
Sorted array is
5 6 7 11 12 13
T(n) = 2T(n / 2) + θ(n)
The above recurrence can be solved either using the Recurrence Tree method or the Master method. It falls in case II of Master Method and the solution of the recurrence is θ(nLogn). Time complexity of Merge Sort is θ(nLogn) in all 3 cases (worst, average and best) as merge sort always divides the array into two halves and takes linear time to merge two halves.
Auxiliary Space: O(n)
Algorithmic Paradigm: Divide and Conquer
Sorting In Place: No in a typical implementation
Stable: Yes
Applications of Merge Sort
- Merge Sort is useful for sorting linked lists in O(nLogn) time. In the case of linked lists, the case is different mainly due to the difference in memory allocation of arrays and linked lists. Unlike arrays, linked list nodes may not be adjacent in memory. Unlike an array, in the linked list, we can insert items in the middle in O(1) extra space and O(1) time. Therefore, the merge operation of merge sort can be implemented without extra space for linked lists.
In arrays, we can do random access as elements are contiguous in memory. Let us say we have an integer (4-byte) array A and let the address of A[0] be x then to access A[i], we can directly access the memory at (x + i*4). Unlike arrays, we can not do random access in the linked list. Quick Sort requires a lot of this kind of access. In a linked list to access i’th index, we have to travel each and every node from the head to i’th node as we don’t have a continuous block of memory. Therefore, the overhead increases for quicksort. Merge sort accesses data sequentially and the need of random access is low. - Inversion Count Problem
- Used in External Sorting
Drawbacks of Merge Sort
- Slower comparative to the other sort algorithms for smaller tasks.
- Merge sort algorithm requires an additional memory space of 0(n) for the temporary array.
- It goes through the whole process even if the array is sorted.
- Recent Articles on Merge Sort
- Coding practice for sorting.
- Quiz on Merge Sort
Other Sorting Algorithms on GeeksforGeeks: 3-way Merge Sort, Selection Sort, Bubble Sort, Insertion Sort, Merge Sort, Heap Sort, QuickSort, Radix Sort, Counting Sort, Bucket Sort, ShellSort, Comb Sort
Merge Sort for Linked Lists
Merge sort is often preferred for sorting a linked list. The slow random-access performance of a linked list makes some other algorithms (such as quicksort) perform poorly, and others (such as heapsort) completely impossible.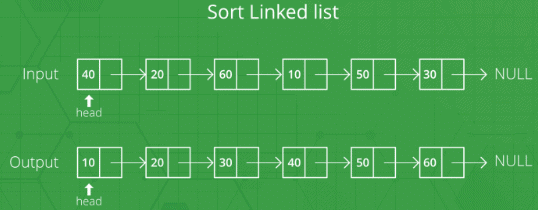
Let the head by the first node of the linked list be sorted and headRef be the pointer to head. Note that we need a reference to head in MergeSort() as the below implementation changes next links to sort the linked lists (not data at the nodes), so the head node has to be changed if the data at the original head is not the smallest value in the linked list.
MergeSort(headRef)
- If the head is NULL or there is only one element in the Linked List then return.
- Else divide the linked list into two halves.
FrontBackSplit(head, &a, &b); /* a and b are two halves */ - Sort the two halves a and b.
MergeSort(a);
MergeSort(b); - Merge the sorted a and b (using SortedMerge() discussed here) and update the head pointer using headRef.
*headRef = SortedMerge(a, b);
C++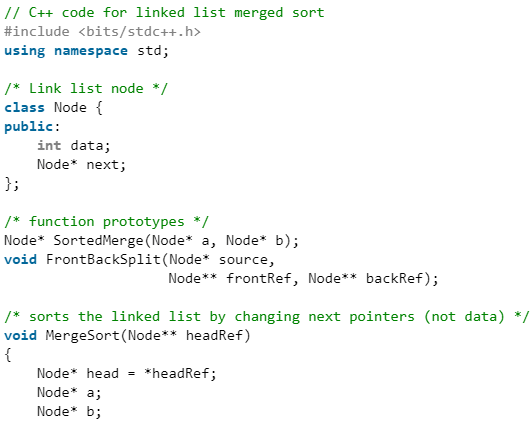






C






Java





Python3



C#





Javascript





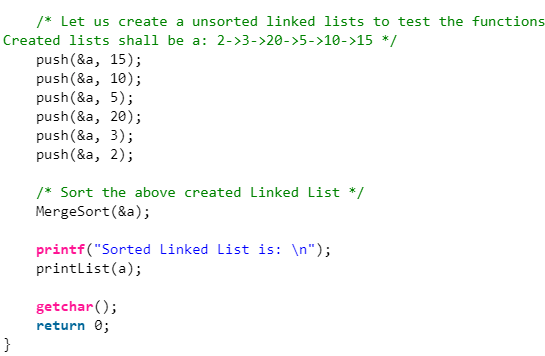
Output:
Sorted Linked List is:
2 3 5 10 15 20
Time Complexity: O(n*log n)
Space Complexity: O(n*log n)}
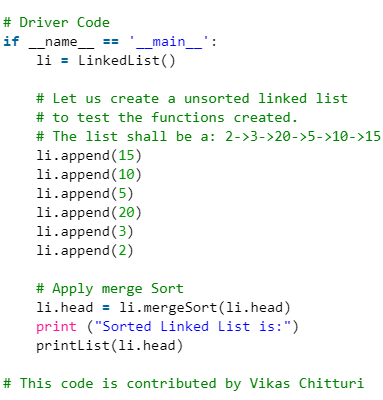
Approach 2: This approach is simpler and uses log n space.
mergeSort():
- If the size of the linked list is 1 then return the head
- Find mid using The Tortoise and The Hare Approach
- Store the next of mid in head2 i.e. the right sub-linked list.
- Now Make the next midpoint null.
- Recursively call mergeSort() on both left and right sub-linked list and store the new head of the left and right linked list.
- Call merge() given the arguments new heads of left and right sub-linked lists and store the final head returned after merging.
- Return the final head of the merged linkedlist.
merge(head1, head2):
- Take a pointer say merged to store the merged list in it and store a dummy node in it.
- Take a pointer temp and assign merge to it.
- If the data of head1 is less than the data of head2, then, store head1 in next of temp & move head1 to the next of head1.
- Else store head2 in next of temp & move head2 to the next of head2.
- Move temp to the next of temp.
- Repeat steps 3, 4 & 5 until head1 is not equal to null and head2 is not equal to null.
- Now add any remaining nodes of the first or the second linked list to the merged linked list.
- Return the next of merged(that will ignore the dummy and return the head of the final merged linked list)
Java





C#





Javascript




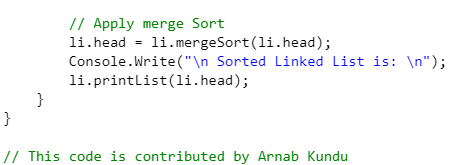
Output:
Sorted Linked List is:
2 3 5 7 10 20
Time Complexity: O(n*log n)
Space Complexity: O(log n)
Merge Sort for Doubly Linked List
Given a doubly linked list, write a function to sort the doubly linked list in increasing order using merge sort.
For example, the following doubly linked list should be changed to 24810
C++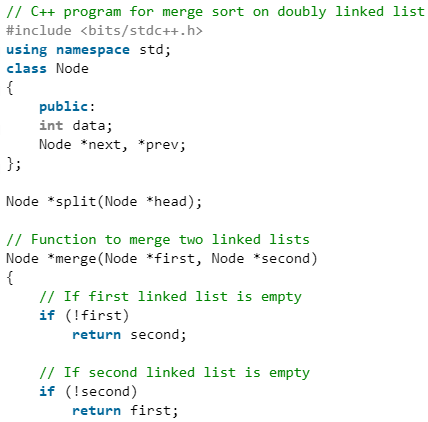





C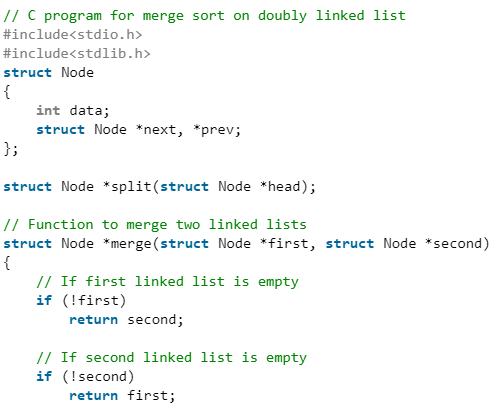





Java




Python




C#





Javascript



Output:
Linked List after sorting
Forward Traversal using next pointer
3 4 5 10 20 30
Backward Traversal using prev pointer
30 20 10 5 4 3
|
81 videos|113 docs|33 tests
|
FAQs on Merge Sort - Algorithms - Computer Science Engineering (CSE)
| 1. What is merge sort for linked lists? |  |
| 2. How does merge sort work for doubly linked lists? |  |
| 3. What is the complexity of merge sort for linked lists? |  |
| 4. Why is merge sort preferred for linked lists over other sorting algorithms? |  |
| 5. Can merge sort be used for sorting arrays as well? |  |
















