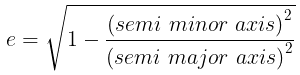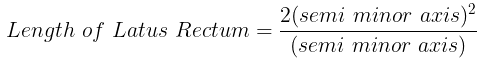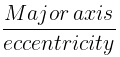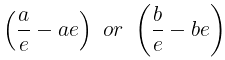Overview: Conic Sections | Applied Mathematics for Class 11 - Commerce PDF Download
| Table of contents |

|
| Introduction |

|
| Terminology |

|
| Circle |

|
| Ellipse |

|
| Parabola |

|
| Hyperbola |

|
| Degenerated Conics |

|
Introduction
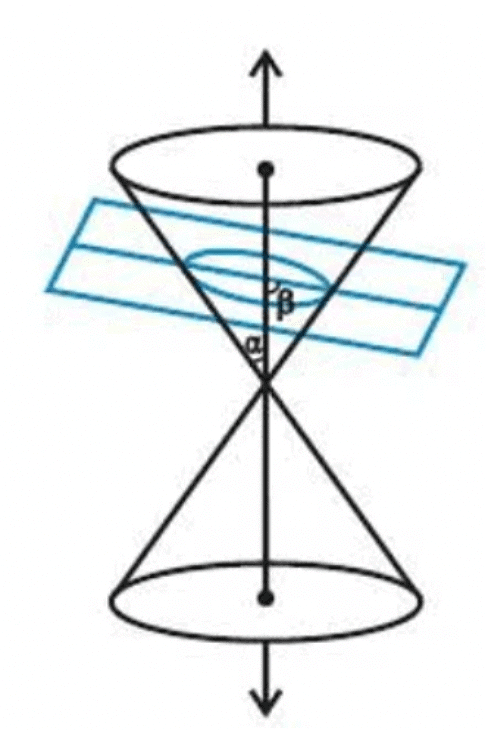
- A curve, generated by intersecting a right circular cone with a plane is termed as ‘conic’.
- It has distinguished properties in Euclidean geometry.
- The vertex of the cone divides it into two nappes referred to as the upper nappe and the lower nappe.
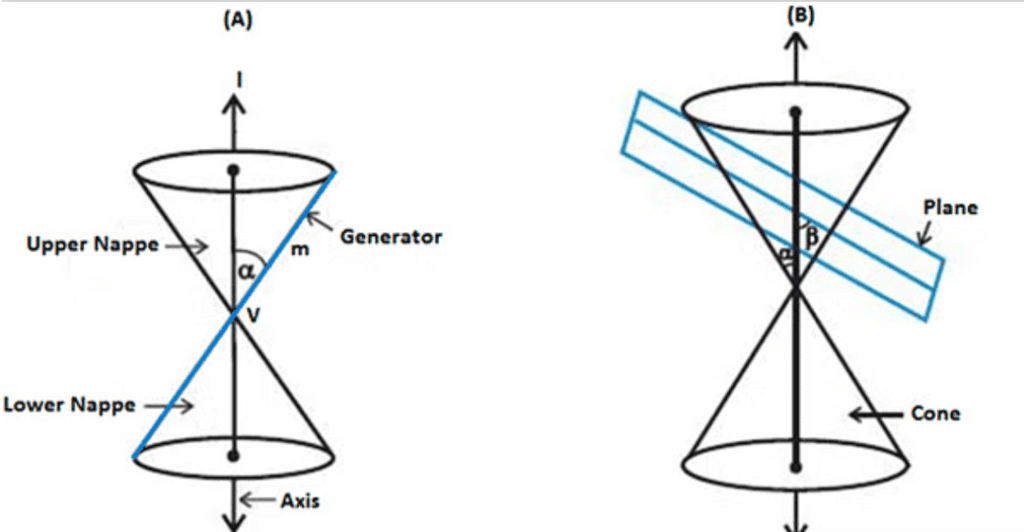
- The initials as mentioned in the above figure A carry the following meaning,
(i) V is the vertex of the cone.
(ii) l is the axis of the cone.
(iii) m, the rotating line is a generator of the cone. - In figure B, the cone is intersected by a plane and the section so obtained is known as a conic section.
Depending upon the position of the plane which intersects the cone and the angle of intersection β, different types of conic sections are obtained. i.e.
(i) Circle
(ii) Ellipse
(iii) Parabola
(iv) Hyperbola
Terminology
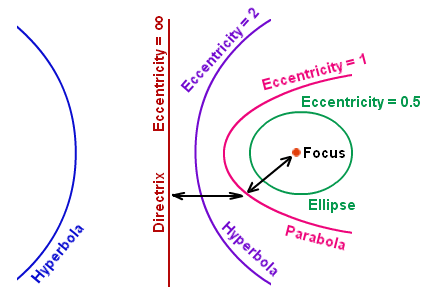
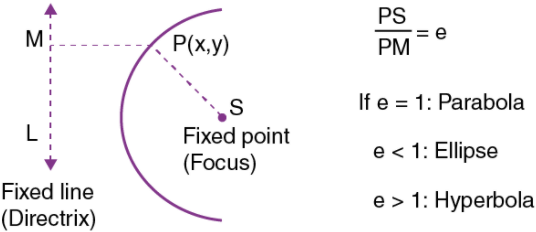
A conic section or conic is the locus of a point that moves in a plane so that its distance from a fixed point is in a constant ratio to its perpendicular distance from a fixed straight line.
- The fixed point is called the Focus.
- The fixed straight line is called the Directrix.
- The constant ratio is called the Eccentricity denoted by e.
- The line passing through the focus & perpendicular to the directrix is called the Axis.
- A point of intersection of a conic with its axis is called a Vertex.
- Eccentricity is the factor related to conic sections which show how circular the conic sections.
More the eccentricity less circular the shape is. The eccentricity of the line is ∞.
The two conic sections will be of the same shape if they have the same eccentricity.
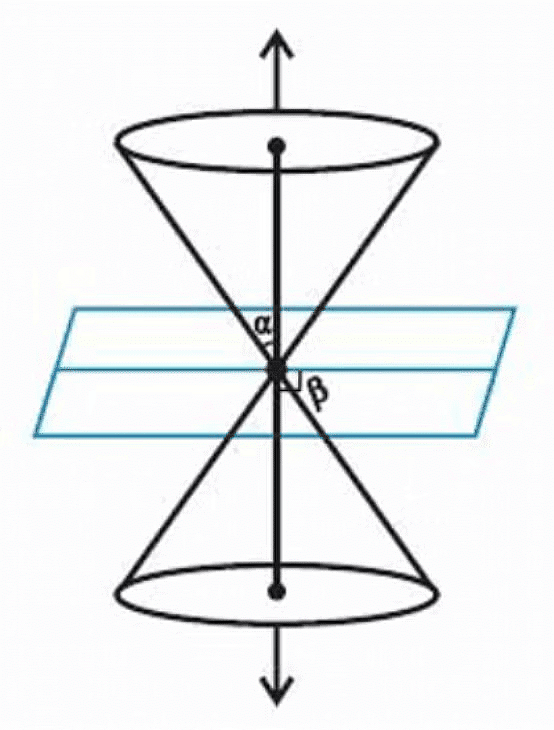
Suppose, the angle formed between the surface of the cone and its axis is β and the angle formed between the cutting plane and the axis is α, then
eccentricity, e = cos α/cos β
Note:
(i) If eccentricity, e = 0, the conic is a circle
(ii) If 0<e<1, the conic is an ellipse
(iii) If e=1, the conic is a parabola
(iv) If e>1, it is a hyperbola
- Principal Axis: Line joining the two focal points or foci of ellipse or hyperbola. Its midpoint is the center of the curve.
- Linear Eccentricity: Distance between the focus and center of a section.
- Latus Rectum: A chord of section parallel to directrix, which passes through a focus.
- Focal Parameter: Distance from focus to the corresponding directrix.
- Major axis: Chord joining the two vertices. It is the longest chord of an ellipse.
- Minor axis: Shortest chord of an ellipse.
Circle
If β=90o, the conic section formed is a circle as shown below.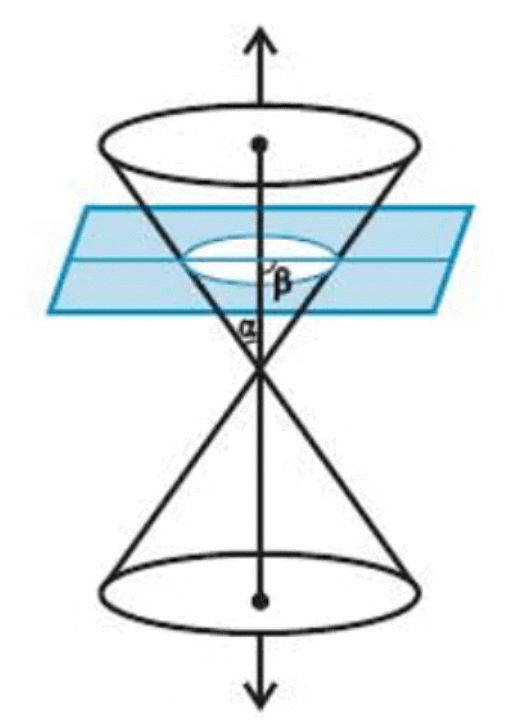
The standard form of a circle: (x - h)2 + (y - k)2 = r2
where (h, k) is the center of the circle and r is the radius of the circle.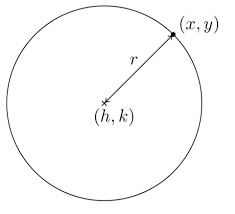
Ellipse
If α<β<90o, the conic section so formed is an ellipse as shown in the figure below.
The standard form of an ellipse is:
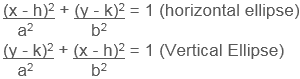
where (h, k) is the center of the ellipse, a is the horizontal stretch factor and b is the vertical stretch factor.
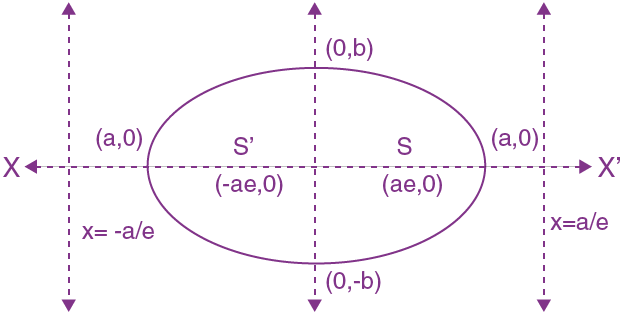 Ellipse with horizontal major axis:
Ellipse with horizontal major axis:
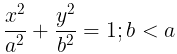
- Focus: There are 2 focii; (ae, 0) and (-ae, 0)
- Directrix: These foci have corresponding directrices as
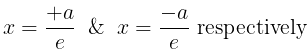
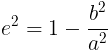
- Length of major axis(xx’): 2a
Length of major axis(yy’): 2b - Vertex: (a, 0) & (-a, 0)
- Centre: (0, 0)
- Latus rectum:
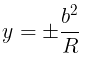
- Length of Latus rectum
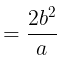
Ellipse with vertical major axis:
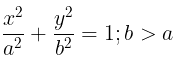
- Focii: (0, be) & (0, -be)
- Directrices: x = b/e & x = -b/e

- Length of major axis (yy'): 2b
Length of minor axis (xx'): 2a - Vertex: (0, b) & (0, -b)
- Centre: (0, 0)
- Latus rectum:
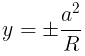
- Length of Latus rectum
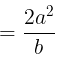
Note:
(i)
(ii)
(iii) Distance between 2 directices=
(iv) Distance between 2 focii = (major axis) × eccentricity
(v) Distance between focus and directrix =
Parabola
If α = β, the conic section formed is a parabola (represented by the orange curve) as shown below.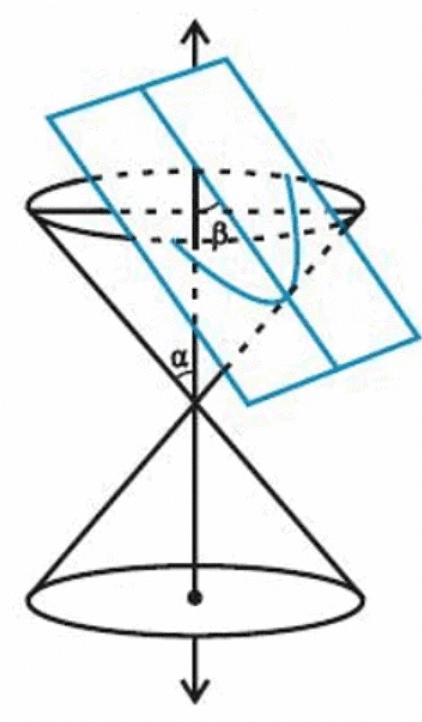
The standard form of an ellipse is:
x = a(y - k)2 + h (east to west), where a is the horizontal stretch factor and (h, k) is the vertex.
y = a(x - h)2 + k (north to south), where a is the vertical stretch factor and (h, k) is the vertex.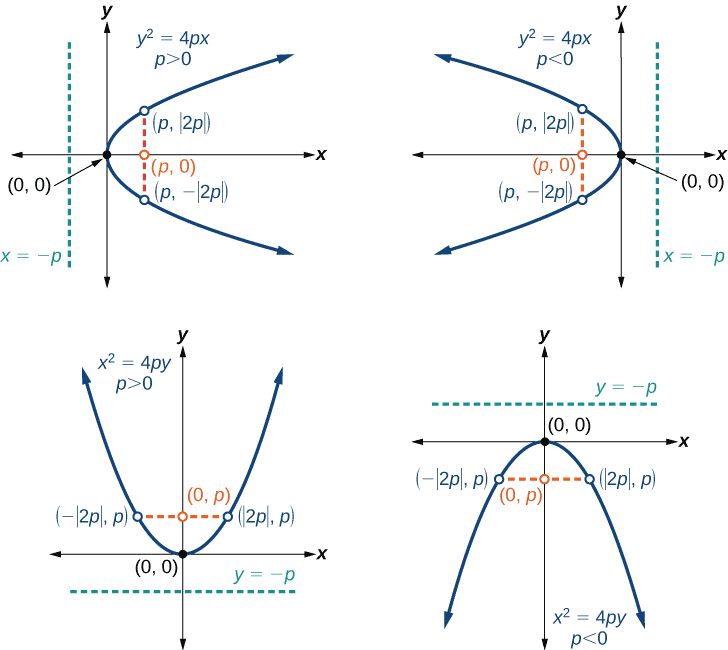 Standard forms of Parabola
Standard forms of Parabola
- Latus rectum: 4 x (distance between vertex and focus) = 4a
- Latus rectum: 2 x Distance between directrix and focus = 2(2a).
- Point of intersection of Axis and directrix and the focus is bisected by the vertex.
- Focus is the midpoint of the Latus rectum.
- (Distance of any point on parabola from the axis)2 = (LR) (Distance of the same point from tangent at the vertex)
Illustration 1: If extreme points of LR are (11/2, 6) and (13/2, 4). Find the equation of the parabola.
Solution: Mid point of LR = focus = (6, 5)
⇒ 4a = 2 or a = ½
The equation of parabolas are: (y – 5)2 = 2(x – 5.5) and (y – 5)2 = – 2 (x – 6.5)
Hyperbola
If 0 ≤ β < α, then the plane intersects both nappes and the conic section so formed is known as a hyperbola (represented by the orange curves).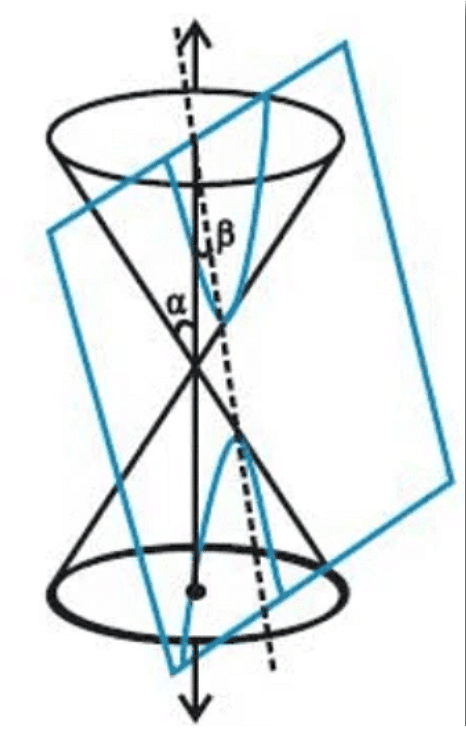
The standard form of an ellipse is: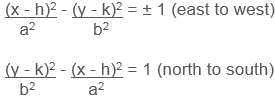
where a is the horizontal stretch factor and b is the vertical stretch factor.
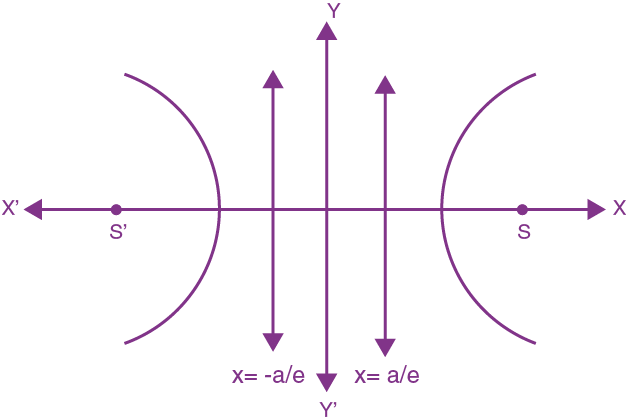
Standard Hyperbola
- Equation:
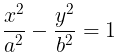
- Focus: There are 2 focii (ae, 0) and (-ae, 0)
- Directrix: The foci has corresponding directrices as x = +a/e and x = −a/e respectively.

- Length of Transverse axis (xx') = 2a
Length of Conjugate axis (yy') = 2b (Hypothetical) - Vertex: (0, 0) and (-a, 0)
- Centre: (0, 0)
- Latus rectum: x = +ae
- Length of latus rectum

- Position of point at hyperbola
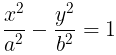 .
.
Let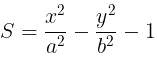 and
and
(i) If S1 > 0, point (x1, y1) lies inside the hyperbola
(ii) If S1 = 0, point (x1, y1) lies on the hyperbola
(iii) If S1 < 0, point (x1, y1) lies outside the hyperbola
Illustration 2: Classify the following equations according to their type of conics.
(a) 4x2 + 4y2 - 16x + 4y - 60 = 0
(b) x2 - 4x + 16y + 17 = 0
(c) x2 + 2y2 + 4x + 2y – 27 = 0
(d) x2 – y2 + 3x – 2y – 43 = 0
Solution:
(a) Here A = 4, B = 0, C = 4
Determinant will be B2 - 4AC = 02- 4(4) (4) = -64
This shows that B2 - 4AC < 0, B = 0 and A = C, so this is a circle.
In another way,
Since Both variables are squared, and both squared terms are multiplied by the same number. Therefore, this is a circle
(b) Here A =1,B = 0, C = 0
Determinant will be B2- 4AC = 02 - 4(1) (0) = 0
This shows that B2 - 4AC = 0, so this is a parabola.
In another way,
Since only one of the variables is squared. Therefore, this is called a Parabola.
(c) Here A =1, B = 0, C = 2
Determinant will be B2 - 4AC = 02 - 4(1) (2) = -8
This shows that B2 - 4AC < 0, and A ≠ C so this is an ellipse.
In other way,
Since both variables are squared with the same sign, but they aren't multiplied by the same number. Therefore, so this is an ellipse.
(d) Here A =1,B = 0, C = -1
Determinant will be B2- 4AC = 02 - 4(1) (-1) = 8
This shows that B2 - 4AC > 0 so this is a hyperbola.
In another way,
Since both variables are squared, and the squared terms have opposite signs. Therefore, this is a hyperbola.
Degenerated Conics
A degenerate conic is generated when a plane intersects the vertex of the cone.
There are three types of degenerate conics:
- If α< β≤90°, then the plane intersects the vertex exactly at a point. This condition is known as the degenerated form of circle or ellipse.
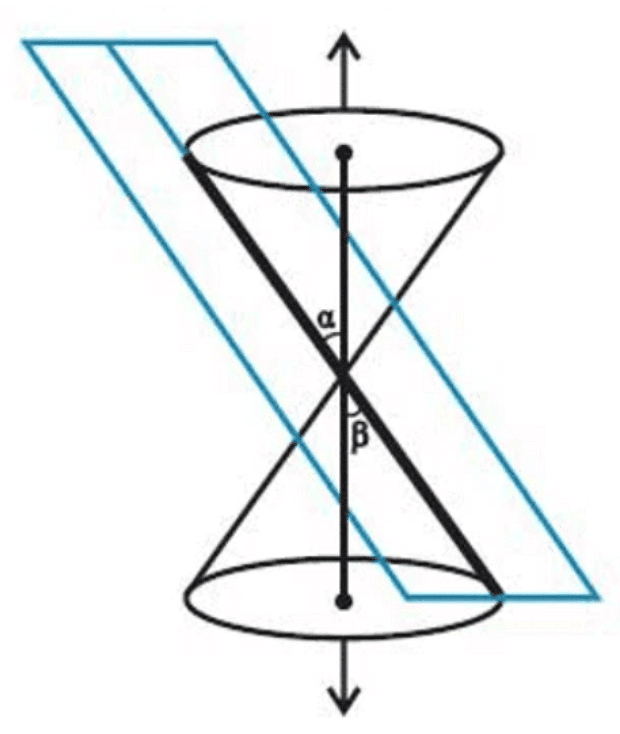
- If α=β, the plane upon an intersection with a cone forms a straight line containing a generator of the cone. This condition is a degenerated form of a parabola.
- If 0≤β<α, the section formed is a pair of intersecting straight lines. This condition is a degenerated form of a hyperbola.

|
83 videos|102 docs|62 tests
|
FAQs on Overview: Conic Sections - Applied Mathematics for Class 11 - Commerce
| 1. What are the key conic sections covered in the JEE syllabus? |  |
| 2. How are circle and ellipse different from each other in terms of their equations and properties? |  |
| 3. What is a degenerated conic in conic sections? |  |
| 4. How are parabolas and hyperbolas distinguished from each other in conic sections? |  |
| 5. How are conic sections used in real-life applications? |  |