De Broglie’s Explanation of Bohr’s Second Postulate of Quantisation | Physics for JEE Main & Advanced PDF Download
Angular Momentum Of Electron
What is Angular Momentum of Electron?
Angular momentum of an electron by Bohr is given by mvr or nh/2π (where v is the velocity, n is the orbit in which electron is, m is mass of the electron, and r is the radius of the nth orbit).
Bohr’s atomic model laid down various postulates for the arrangement of electrons in different orbits around the nucleus. According to Bohr’s atomic model, the angular momentum of electron orbiting around the nucleus is quantized. He further added that electrons move only in those orbits where angular momentum of an electron is an integral multiple of h/2. This postulate regarding the quantisation of angular momentum of an electron was later explained by Louis de Broglie. According to him, a moving electron in its circular orbit behaves like a particle wave.
De Broglie’s Explanation to the Quantization of Agular Momentum of Electron:
The behaviour of particle waves can be viewed analogously to the waves travelling on a string. Particle waves can lead to standing waves held under resonant conditions. When a stationary string is plucked, a number of wavelengths are excited. On the other hand, we know that only those wavelengths survive which form a standing wave in the string, that is, which have nodes at the ends.
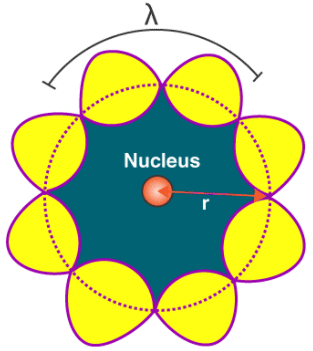 Quantization of Angular Momentum of Electron
Quantization of Angular Momentum of Electron
Thus, in a string, standing waves are formed only when the total distance travelled by a wave is an integral number of wavelengths. Hence, for any electron moving in kth circular orbit of radius rk, the total distance is equal to the circumference of the orbit, 2πrk.
2πrk = kλ
Let this be equation (1).
Where,
λ is the de Broglie wavelength.
We know that de Broglie wavelength is given by:
λ = h/p
Where,
p is electron’s momentum
h = Planck’s constant
Hence,
λ = h/mvk
Let this be equation (2).
Where mvk is the momentum of an electron revolving in the kth orbit. Inserting the value of λ from equation (2) in equation (1) we get,
2πrk = kh/mvk
mvkrk = kh/2π
Hence, de Broglie hypothesis successfully proves Bohr’s second postulate stating the quantization of angular momentum of the orbiting electron. We can also conclude that the quantized electron orbits and energy states are due to the wave nature of the electron.
|
291 videos|648 docs|183 tests
|
FAQs on De Broglie’s Explanation of Bohr’s Second Postulate of Quantisation - Physics for JEE Main & Advanced
| 1. What is the formula to calculate the angular momentum of an electron? |  |
| 2. How does De Broglie explain Bohr's second postulate of quantisation? |  |
| 3. What is the significance of Bohr's second postulate of quantisation? |  |
| 4. How does the De Broglie wavelength relate to the quantisation of electron motion? |  |
| 5. Can the angular momentum of an electron in an atom have any value? |  |






















