Volume & Capacity | Mathematics (Maths) Class 8 PDF Download
| Table of contents |

|
| What is Volume? |

|
| What is capacity? |

|
| Mensuration of Some Enclosed Figures |

|
| Sample Problems on Volume and Capacity |

|
Mensuration is the branch of mathematics that talks about the length, volume, and area of different geometrical objects. The shape may be in 2-D or 3-D. We find the volume of 3-D objects and area of 2-D objects.
What is Volume?
Volume is the measurement of total space occupied by a given solid. Volume is defined in 3-D because to have the volume the object must have three variables i.e. length, breadth or thickness or width, and height.
The difference between the total amount of space left inside the hollow body and the space occupied by the body is the volume of the figure. Now, let us take the example of a 3d shape called cuboid, it is a solid figure bounded by six rectangles and thus has six rectangular faces. The dimensions of the cuboid are as follows: length l, breadth b, and height h.height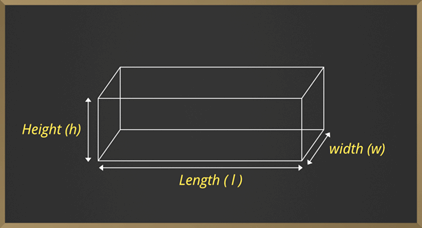
Volume of the cuboid is given as:
Volume = length * height * width
Volume is for both solid and hollow objects. E.g. Cube, Cuboid, Cone, Cylinder, etc.
What is capacity?
When the hollow object is filled with liquid or air and it takes the shape of that object or container. The total volume of the water and air which is filled inside the container is called the capacity of the container.
Note: Capacity is calculated only for hollow object.
Example: Cone, Cylinder, Hollow hemisphere, etc.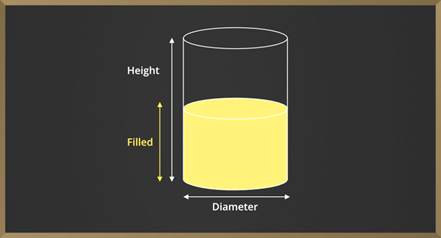
Example: Find the volume and capacity of cylinder whose radius is 14 cm and height is 21cm.
Solution: We have given, r = 14cm, h = 21cm;
Volume of cylinder = πr*r*r*h.
V = 22/7 * 14 * 14 * 21
V = 12,936cm3.
and capacity is = 12,936/1000 litre …….as (1000cm3= 1litre)
= 12.936 litre.
Note: The unit of capacity is litres(l) and millilitres(ml).
Mensuration of Some Enclosed Figures
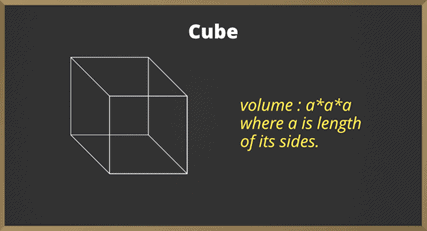
Cube
Surface area of cube is defined as the area of every face of the cube. For e.g. as we know that every side of cube is equal. So area of one face is length*length or width*width or height*height out of these three we pick one according to question.
So total surface area of cube is 6 * length * length. Because cube has six faces and each face has an area of length*length.
Now the volume of cube is its hollow portion and can be written as length * length * length or width * width * width or height * height * height. And its unit will be cubic.
Example: Find the width of the cube whose volume is 625cm3.
Solution:
We know that volume of the cube is a * a * a =a3 where a can be the length, width, height.
So, a3 = 125 then
a = 5cm ( 5 is cube root of 125)
So width is 5 cm.
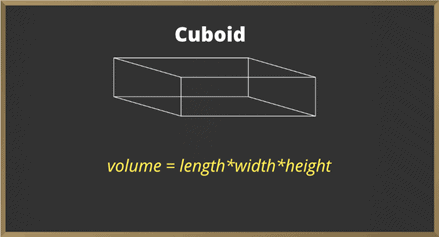
Cuboid
Surface area of cuboid is defined as the surface area of cube but the difference here is all the sides are not equal and in cuboid length width height are different. So its surface area will be the area of each face and add all the areas which we will get total surface area.So total surface area of cuboid is length * width + width * height + height * length + length * width + width * height + height * length i.e. the addition of areas of every six face
So total surface area is
2 * (length * width + width * height + height * length)
The volume of cuboid is the hollow portion inside the cuboid and it is
Volume = length * width * height
Example: Find the height of cuboid volume is 625cm3 and its base area is 25 cm2.
Solution:
Base area of cube means width * length this forms base in cube
As we know volume of cube is
=> l * b * h = 625
=> h = 625 / b * l
=> h = 625 / 25
=> h = 25cm
So the height is 25 cm
Cylinder
Here we are talking about right circular cylinder for e.g. round pillar, tube lights, water pipes, etc. Volume of cylinder is the hollow portion inside the cylinder.
Volume of Cylinder = 22/7 * r * r * h
Here,
r = radius of cylinder and h = height of cylinder

Example: A rectangular sheet of paper having length 11cm and width 4cm cm is being rolled to form a cylinder of height 4 cm. What is the volume of the cylinder
Solution:
Let the cylinder if radius = r and its height = h
Perimeter of base of cylinder = 2 * pi * r = 11cm
=> 2 * 22/7 * r = 11cm
=> r = 7/4 cm
Volume = 22/7 * r* r * h
=> 22/7 * 7/4 * 7/4 * 4
=> 38.5cm3
Hence, the volume of cylinder is 38.5cm3
Cone
Volume of cone is the hollow portion inside cone.
Volume = 1/3 * 22/7 * r * r * h
Here,
h = height of cone
r = radius of cone

Sample Problems on Volume and Capacity
Sample Problems on Volume and Capacity
Problem 1: Find the capacity, in litres, of cubic tank with length, width, height is given as 1 m, 1m, and 1m respectively.
Solution:
First we convert between volume and capacity in cm3 and ml so we need to find volumes in cm3
The volume is 1m * 1m * 1m = 1m3 as it is cube so we used cube formula
As 1m = 100cm so volume in cm3 is 100cm * 100cm * 100cm = 1000000cm3
As 1cm3 = 1ml So the capacity of the tank in ml is 1000000ml.
and finally capacity of tank in litre is 1000000/1000=1000litres.
As 1000ml is 1 litre. So the capacity of tank is 1000litres.
Problem 2: A tank measures 2m, 1m, 2m. Find the capacity of tank.
Solution:
As we know that 1m = 100cm.
As it is cuboid figure because its length is different.
Volume of cuboid = length * width * height = 2m * 1m * 2m = 4m3.
Or 200cm * 100cm * 200cm = 4000000cm3.
We know that, 1cm3 = 1ml so 4000000cm3 = 4000000ml
As 1000ml = 1litre, then 4000000ml is 4000000/1000 = 4000 litres is capacity of tank.
Problem 3: A rectangular sheet of paper is being rolled and converted to cylinder of radius 10cm what is the volume of cylinder? Width of rectangle is 7cm.
Solution:
Width of the rectangle becomes the height of the cylinder and the radius of the cylinder is given as 10 cm.
So the value of cylinder is V = 22/7 * r * r * h
V = 22/7 * 10 * 10 * 7
v = 22 * 10 * 10
v = 2200cm3.
Problem 4: What is the volume of the cone if the radius is 9cm and height is 14cm
Solution:
The volume of cone = 1/3 * pi * r * r * h
Hence, volume is 1/3 * 22/7 * 9 * 9 * 14
1 * 22 * 3 * 9 * 2 = 1,188cm3.
|
81 videos|423 docs|31 tests
|
FAQs on Volume & Capacity - Mathematics (Maths) Class 8
| 1. What is the difference between volume and capacity? |  |
| 2. How do you calculate the volume of a cube? |  |
| 3. What is the formula for finding the volume of a cylinder? |  |
| 4. How can you measure the capacity of a container? |  |
| 5. How does the volume of a rectangular prism differ from that of a cylinder? |  |




















