Area of Triangle | Mathematics (Maths) Class 7 (Old NCERT) PDF Download
Area of Triangle
The area of a triangle is defined as the total space occupied by the three sides of a triangle in a 2-dimensional plane. The area of a triangle is equal to half of the base times height, i.e. A = 1/2 x b x h. Hence, to find the area of a triangle, we need to know the base (b) and height (h) of it. This formula is applicable to all types of triangles, whether it is scalene, isosceles or equilateral. Remember the base and height of a triangle are perpendicular to each other.
In this lesson, we will learn the area of triangle formulas for different types of triangles, along with some examples.
What Is the Area of a Triangle?
The area of a triangle is the region enclosed between the sides of the triangle. Every possible triangle will have some area. Depending on the length of the sides and the internal angles, the area of a triangle varies from one triangle to another. The unit of area is measured in square units, for example, m2, cm2, in2, etc.
Area of a Triangle Formula
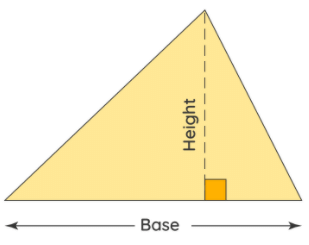
Area = 1/2 x Base x perpendicular Height
There are many ways to find the area of a triangle. Apart from the above formula, Heron’s formula is used to calculate the triangle’s area, when we know the length of all three sides. Also, trigonometric functions are used to find the area when we know two sides and the angle formed between them in a triangle.
We will calculate the area for all the conditions in this article.
Example: What is the area of a triangle with base b = 2 cm and height h = 4 cm?
Using the formula,
Area of a Triangle, A = 1/2 x b x h = 1/2 x 4 cm x 2 cm = 4 cm2
Triangles can be classified based on their angles as acute, obtuse, or right triangles. They can be scalene, isosceles, or equilateral when classified based on their sides.
Area of Triangle Using Heron's Formula
Heron's formula is used to find the area of a triangle when the length of the 3 sides of the triangle is known. The perimeter of a triangle is the distance covered around the triangle and is calculated by adding the lengths of all three sides of a triangle.
Heron’s formula has two important steps. The first step is to find the semi perimeter (half perimeter) of a triangle by adding all the three sides of a triangle and dividing it by 2. The next step is to apply the semi-perimeter of triangle value in the main formula called “Heron’s Formula” to find the area of a triangle.
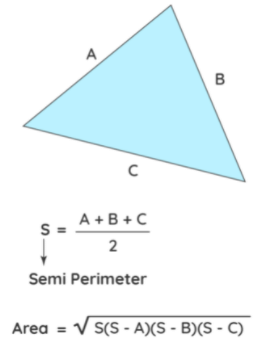 Heron's FormulaConsider the triangle ABC with side lengths A, B, and C. Heron's formula to find the area of the triangle is:
Heron's FormulaConsider the triangle ABC with side lengths A, B, and C. Heron's formula to find the area of the triangle is:
Area = 
Note that (A + B + C) is the perimeter of the triangle.
'S' is the semi-perimeter which is given by (A + B + C)/2
Area of Triangle With 2 Sides and Included Angle (SAS)
There are three variations to the same formula based on which sides and included angle are given. Consider the triangle,
 Area of a triangle with 2 sides and an included angle(SAS)
Area of a triangle with 2 sides and an included angle(SAS)
When sides 'b' and 'c' and included angle A is known, the area of the triangle is:
Area (∆ABC) = 1/2 x bc x sin(A)
When sides 'b' and 'a' and included angle B is known, the area of the triangle is:
Area (∆ABC) = 1/2 x ab x sin(C)
When sides 'a' and 'c' and included angle C is known, the area of the triangle is:
Area (∆ABC) = 1/2 x ac x sin(B)
These formulas are very easy to remember and also to calculate.
Example: In ∆ABC, A = 30° and b = 4, c = 6 in units. Then the area will be;
Area (∆ABC) = 1/2 bc sin A
= 1/2 (4) (6) sin 30º
= 12 x 1/2 (since sin 30º = 1/2)
= 6 sq.unit.
How To Calculate the Area of a Triangle?
The area of the triangle can be calculated using the formulas as discussed above or using the area of triangle calculator. The area formulas for all the different types of triangles like an area of an equilateral triangle, right-angled triangle, and isosceles triangle are given below.
Area of a Right Angled Triangle
A right-angled triangle, also called a right triangle, has one angle at 90° and the other two acute angles sums to 90°. Therefore, the height of the triangle will be the length of the perpendicular side.
Area of a Right Triangle = A = 1/2 x Base x Height (Perpendicular distance)
Area of an Equilateral Triangle
An equilateral triangle is a triangle where all the sides are equal. The perpendicular drawn from the vertex of the triangle to the base divides the base into two equal parts. To calculate the area of the equilateral triangle, we have to know the measurement of its sides.
Area of an Equilateral Triangle = A = (√3)/4 x side2
Area of an Isosceles Triangle
An isosceles triangle has two of its sides equal and also the angles opposite the equal sides are equal.
Area of an Isosceles Triangle = 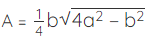
where 'b' is the base and 'a' is the measure of equal side.
A table with all the formulas for area of a triangle is given below:

Solved Examples on Area of Triangle
Example 1: Find the area of an acute triangle with a base of 10 inches and a height of 5 inches.
Solution: A = (1/2) x b x h sq.units
A = (1/2) x (10 in) x (5 in)
A = (1/2) x (50 in2)
A = 25 in2
Example 2: Find the area of a right-angled triangle with a base of 9 cm and a height of 11 cm.
Solution:
A = (1/2) x b x h sq.units
A = (1/2) x (9 cm) x (11 cm)
A = (1/2) x (99 cm2)
A = 49.5 cm2
Example 3: Find the area of an obtuse-angled triangle with a base of 8 cm and a height 7 cm.
Solution:
A = (1/2) x b x h sq.units
A = (1/2) x (8 cm) x (7 cm)
A = (1/2) x (56 cm2)
A = 28 cm2
|
77 videos|386 docs|39 tests
|
FAQs on Area of Triangle - Mathematics (Maths) Class 7 (Old NCERT)
| 1. What is the formula to calculate the area of a triangle? |  |
| 2. How do you find the base and height of a triangle? |  |
| 3. Can I use the area of a triangle formula for any type of triangle? |  |
| 4. Is it possible to calculate the area of a triangle if only the lengths of its sides are given? |  |
| 5. Can the area of a triangle be negative? |  |





















