Superposition of Two or More Simple Harmonic Oscillators: Notes with Example | Oscillations, Waves & Optics - Physics PDF Download
Superposition of Two Collinear Harmonic Oscillations
Addition of Two S.H.M having Equal Frequencies
Consider two SHMs of equal frequencies but of different amplitudes and phase constants
acting on a particle in the x -direction.
The displacement x1 and x2 of the two SHM of frequency ω is
x1 = A1 sin (ωt +φ1) and x2 = A2 sin (ωt +φ2)
where A1 and A2 are the amplitude and φ1 and φ2 the initial phases of the two motions.
The resultant displacement x at any instant t is
x = x1 + x2 = A1 sin (ωt +φ1) = A2 sin (ωt +φ2)
⇒ x = A2 sin ωt +φ2 = A1(sinωt cosφ1 + cosωt sinφ1) + A2 (sinωt cosφ2 + cosωtsinφ2)
⇒ x = sinωt (A1 cosφ1 + A2 cosφ2) + cosωt (A1sinφ1 + A2sinφ2)
Now Let
A1 cosφ1 + A2 cosφ2 = Acosδ and A1 sinφ1 + A2sinφ2 = Asinδ
where A and δ are constant to be determined.
⇒ x = Asin (ωt +δ )
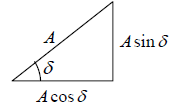
This shows that the resultant motion is SHM with angular frequency ω, the same as that
of the individual SHMs.
The resultant motion has amplitude A and a phase constant δ
where A =  and
and 
Conclusion: superposition of collinear SHM is also a SHM of the same frequency but
different amplitude and phase constant
Case-I: (Maximum Amplitudes)
When the phase difference between the two individual motions is zero or any integral
multiple of 2π i.e. φ1 −φ2 = 2nπ n = (0,1, 2,3...)
Then A = A1 + A2 (Resultant amplitude is sum of the amplitudes of individual motions)
Case-I: (Minimum Amplitudes)
Whenφ1 −φ2 = (2n +1)π , n = (0,1, 2,3...) this gives A = A1 − A2
If A1 = A2 then A = 0 , i.e particle at rest.
Addition of Two S.H.M having Different Frequencies
Consider two SHM of equal amplitude but different frequencies
x1= A1 sinω1 t and x2 = A2 sinω2 t
The resultant displacement is
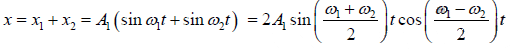
x = 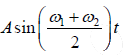
This represent a periodic motion) of amplitude A = 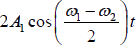
⇒ 
Thus resultant amplitude of motion varies periodically between 1 ±2A and zero.
The amplitude A is maximum when 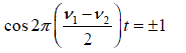
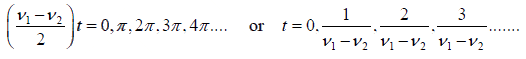
Hence the time interval between two consecutive maxima is Tb = 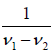 .
.
The frequency νb of maxima is = ν1 −v2
The amplitude A is minimum when 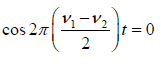
or 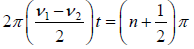 (n = 0,1,2,3....)
(n = 0,1,2,3....)
or 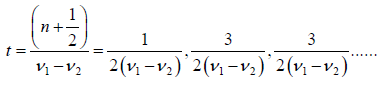
Thus the time interval between two consecutive minima is Tb = 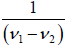
Hence the frequency of minima is also (ν1 −v2) .
One maximum of amplitude followed by a minimum is called a beat. The time period Tb
between the successive beats is called the beat period Tb = 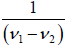 and beat frequency
and beat frequency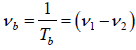
Superposition of Two Perpendicular Harmonic Oscillations
Addition of Two SHM having Equal Frequencies
Let us consider two perpendicular SHM one along x -axis and other along y -axis with
amplitude A1 & A2
x = A1 sin ωt +δ and y = A2 sinωt where δ is phase constant.
⇒ 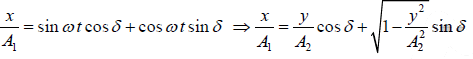
∵ sin ωt = y/A2 and cosωt = 
⇒ 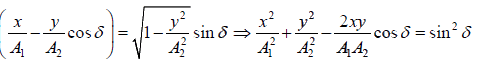
This is the general equation of ellipse whose axes are inclined to the co-ordinate axes.
Let us consider few cases
(i) δ = 0 ⇒ 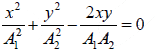
or 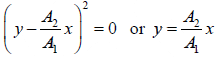
This is the equation of straight line having a positive slope A2/A1 and passing through the origin.
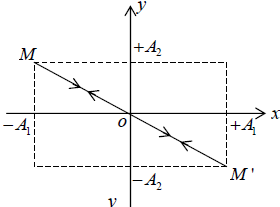
Motion description: x = A1 sinωt and y = A2 sinωt
At time t = 0 , particle is at O, at t = 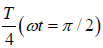 , particle is at M .
, particle is at M .
At t = 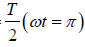 , =π , particle is at O, at t =
, =π , particle is at O, at t = 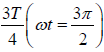 , particle is at M′ .
, particle is at M′ .
and at t = T (ωt = 2π ) , particle is at O
Such vibration is called linearly polarized vibration.
(ii) δ = π/2 ⇒ 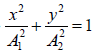 which is equation of ellipse as shown in figure .The particle
which is equation of ellipse as shown in figure .The particle
moves in an elliptical path. The direction of its motion can be obtained as
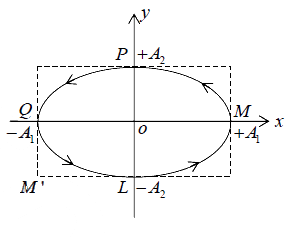
x = A1 cosωt and y = A2 sinωt
At 1 t = 0, (ωt = 0) : x = A1 , y = 0 i.e. particle is at M
At t = 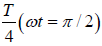 : x = 0, y = +A2 i.e. particle is at P
: x = 0, y = +A2 i.e. particle is at P
At t =  : x = −A1 y = 0 i.e. particle is at Q
: x = −A1 y = 0 i.e. particle is at Q
At t = 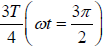 :x =0, y= −A2 i.e. particle is at L
:x =0, y= −A2 i.e. particle is at L
At t = T (ωt = 2π) : x = +A1 , y = 0 i.e. particle is at M
Thus the particle traces out an ellipse in the anti-clockwise direction. Such vibration is
called LEFT-HANDED elliptically polarized vibration.
In addition, If A1 = A2 = A , the motion become circular ( x2 + y2 = A2 ) with radius A .
(iii) δ = π ⇒ 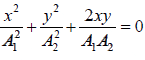
or 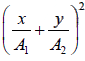 = 0 y =
= 0 y = 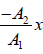
This represents a equation of straight line, having negative slope -A2/A1 & passing through the origin.
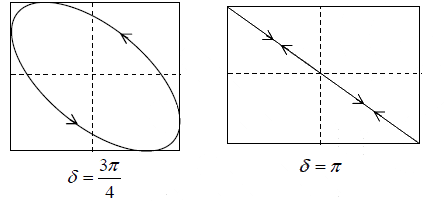
(iv) δ = 3π/2 = 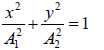
Such vibration is called RIGHT-HANDED elliptically polarized vibration.
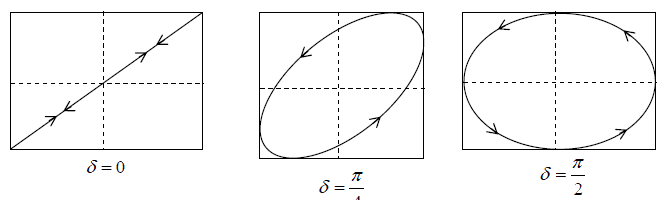
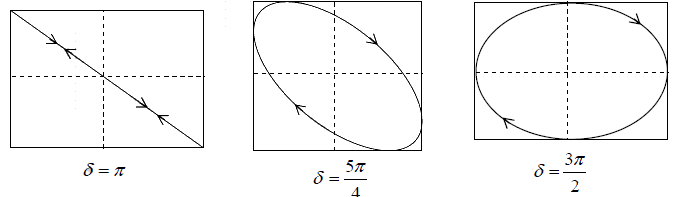
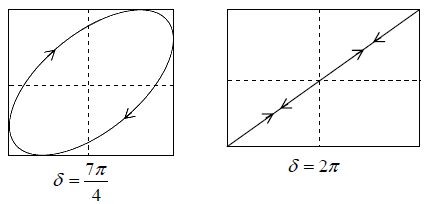
Addition of Two SHM having Different Frequencies (Lissajous Figures)
Frequencies in the Ratio of 2:1
Let a particle is subjected to two mutually perpendicular SHM having frequencies
ω1 :ω2 = 2 :1
x = A1sin (2ωt +δ) and y = A2 sinωt
Where A1 & A2 are the amplitude of the x -vibrations & y -vibration and δ is the phase
difference between them.
The equation of the curve of resultant motion is obtained as
x/A1 = sin2ωt cosδ + cos2ωt sinδ = 2sinωt cosωt cosδ + (1 - 2sin2ωt)sinδ
= 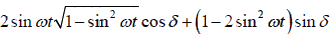
⇒ 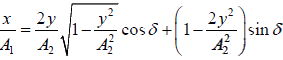 .
.
⇒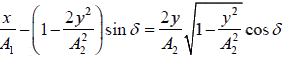
⇒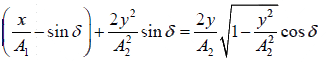
Squaring and re-arranging terms, we get
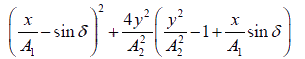 = 0
= 0
This is the general equation of curve having two loops
(i) Whenδ = 0 , sinδ = 0 , thus
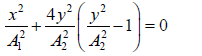
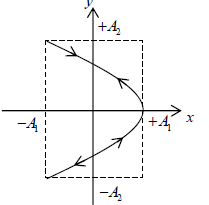
This represents a curve symmetrical about both the axes.
(ii) When δ = π/2, sinδ = 1
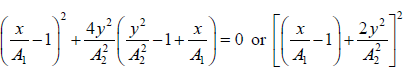 = 0
= 0
This represents two coincident parabolas symmetrical about the x-axis and their vertices
at (A1 ,0) . The equation of Parabola is

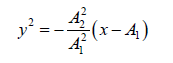
(iii) when δ =π , sinδ = 0 . The case is similar to case (i).
(iv) when δ =3π/2 , sinδ = -1
so, 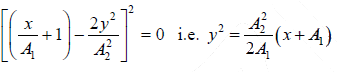
This represent parabola symmetric about the x -axis with their vertices at(-A1 ,0) .
Following figures shows the Lissajous figures for various initial phase differences for
frequency ratio 2:1
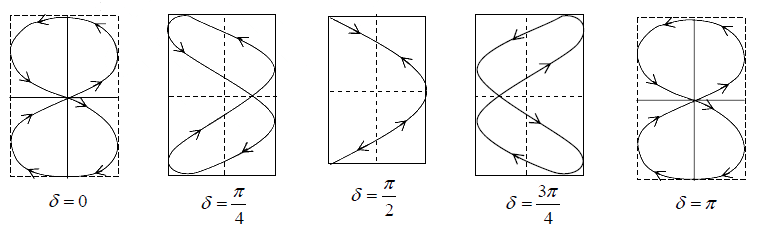
Note: If particles displacements are of following form
x = A1sin(2ωt) and y = A2sin(ωt + δ)
The resultant Lissajous figures loops will be
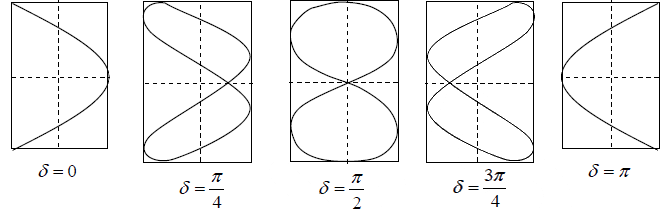
(2) Frequencies in the ratio of 3:1
For x = A1sin (3ωt +δ) and y = A2sinωt
The resultant Lissajous figures at various initial phase differences are
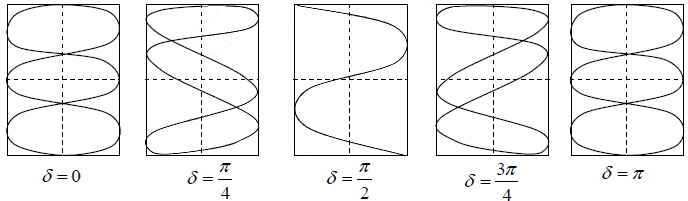
Method to find the frequencies ratio:
To find the frequencies ratio from the given Lissajous figure, draw two lines parallel to x
and y axis which having maximum intercept with loops.
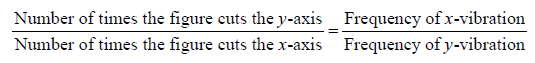
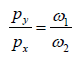
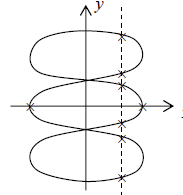
In above figure, py = 6 & px = 2 ⇒ω1 :ω2 = 3:1
|
54 videos|22 docs|14 tests
|
FAQs on Superposition of Two or More Simple Harmonic Oscillators: Notes with Example - Oscillations, Waves & Optics - Physics
| 1. What is the superposition of two collinear harmonic oscillations? |  |
| 2. How do we mathematically represent the superposition of two collinear harmonic oscillations? |  |
| 3. What happens when two collinear harmonic oscillations have the same frequency and phase difference? |  |
| 4. How does the superposition of two perpendicular harmonic oscillations differ from collinear oscillations? |  |
| 5. Can the superposition of two perpendicular harmonic oscillations result in a zero displacement? |  |





















