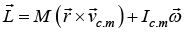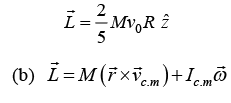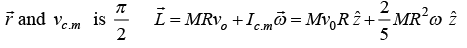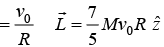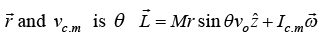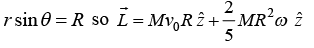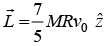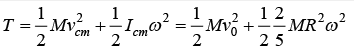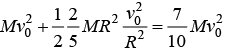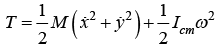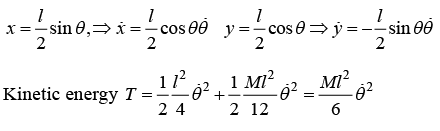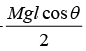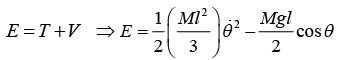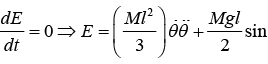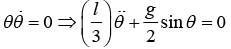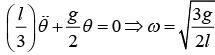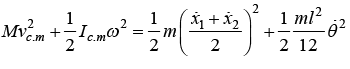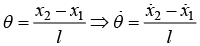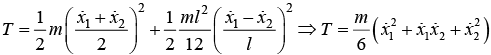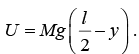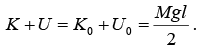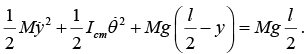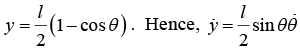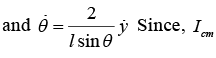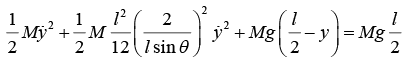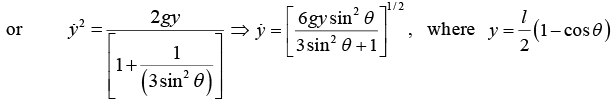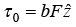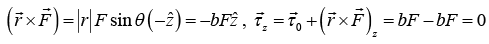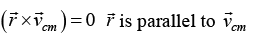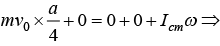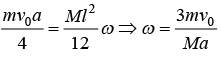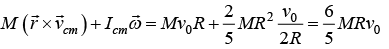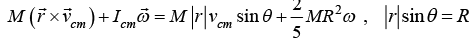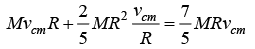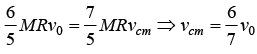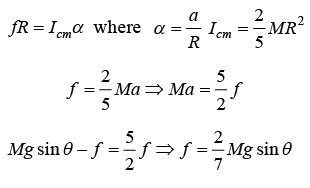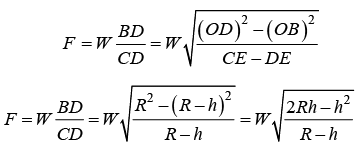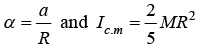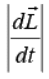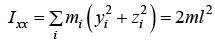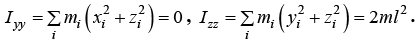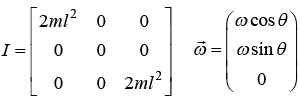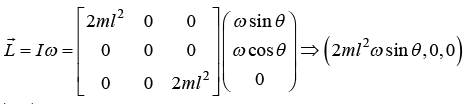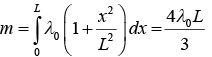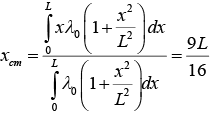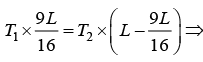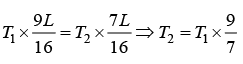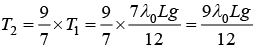Rotational Dynamics | Mechanics & General Properties of Matter - Physics PDF Download
Angular Momentum Due to Particle
The particle has momentum 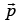 , then angular momentum about point O is given
, then angular momentum about point O is given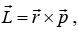 , where
, where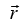 is position vector of particle with respect to origin. Consider motion in the x-y plane, first in the x - direction and then in the y - direction, as shown below in figure (a) and (b).
is position vector of particle with respect to origin. Consider motion in the x-y plane, first in the x - direction and then in the y - direction, as shown below in figure (a) and (b).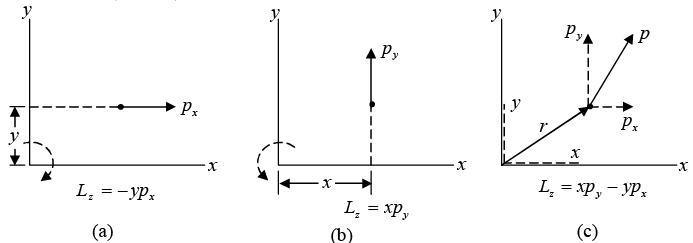
The most general case involves both these motions simultaneously, as shown in above figure. Hence, Lz = xpy - ypx
As you can verify by inspection or by evaluating the cross product as follows. Using r = (x, y, 0) and p = (px, Py, 0), we have
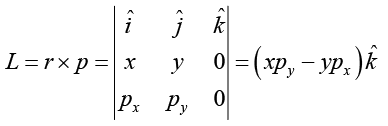
Motion of a rigid body involving translation and rotation
Assume a sphere of mass M and radius R are rolling on a rough surface, where vcm is velocity of center of mass and ω is angular velocity
Pure translation: when sphere perform pure translation motion then every point has same speed of speed of center of mass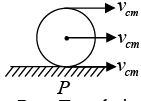 Pure Rotation: when sphere perform pure rotation about center of mass then center of mass have zero velocity and all other point have velocity
Pure Rotation: when sphere perform pure rotation about center of mass then center of mass have zero velocity and all other point have velocity 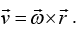
so upper and lower points have v = ωR but in opposite direction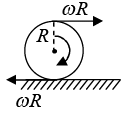 Rolling - when translation and rotation can be combined then sphere will rolling
Rolling - when translation and rotation can be combined then sphere will rolling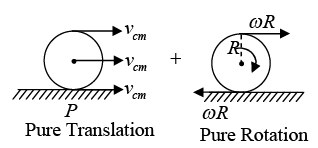
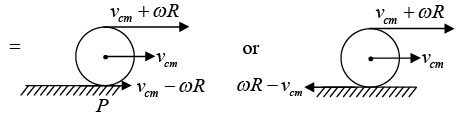
The condition of Rolling without slipping
A rigid body such as sphere having translation motion as velocity of center of mass vcm and angular velocity about center of mass is ω. The condition of rolling without slipping will achieve if vcm = ωR where R is radius of rolling body.
Similarly, if acceleration of center of mass is acm and α is angular velocity of about center of mass then acm = ωR , where R is radius of rolling body.
Angular Momentum of Rigid body involve Rolling
The angular momentum About any point O of rigid body of mass M and radius R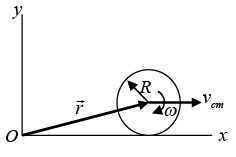
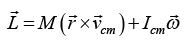
Where 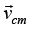 is velocity vector of center of mass
is velocity vector of center of mass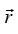 is position vector of center of mass from origin O
is position vector of center of mass from origin O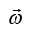 is angular velocity about center of mass
is angular velocity about center of mass
Ic.m is moment of inertia about center of mass
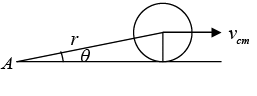
Example 1: A sphere of mass M and radius R having velocity of center of mass v0 . As friction of surface is enough so that sphere Achieving condition of rolling without slipping.
(a) Find the angular momentum about Center of mass C
(b) Find the Angular momentum about point of contact P
(c) Find Angular momentum about Point O
(a)
for rolling without slipping, vc.m = ωR ω = V0/R
|r| = R and angle between
for rolling without slipping, vc.m = ωR ω
(c)
|r| = r and angle between
For rolling without slipping, vc.m = ωR ω = v0/R
Kinetic Energy of Rigid Body
The rigid body of mass M and radius R . The moment of inertia about center of mass is Icm. The velocity of center of mass is vcm and angular velocity about center of mass is ω, then kinetic energy is 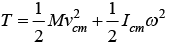
Example 2: A sphere of mass M and radius R having velocity of center of mass v0. As friction of surface is enough so that sphere Achieving condition of Rolling without Slipping . Find the kinetic energy of sphere.
Rolling without slipping, vc.m = ωR ω = V0/R 1/2
Example 3: A rod of length l is pivoted at one of its end. If rod is constrained to move in y - z plane, then
(a) find the total energy of system
(b) find angular frequency for small oscillation.
(a)
Potential energy V is given by (θ) = -
(b) Hence, energy is conserved
for small oscillation, sinθ = θ , so
Example 4: A rod of mass m and length l is suspended from two mass less vertical springs with a spring constants k1 and k2. If x1 and x2 be the displacements from equilibrium position of the two ends of the rod, find the kinetic energy of system.
T = 1/2
for small oscillation
(keep in mind that there is not pure rotation case)
Example 5: A stick of length l and mass M initially upright on a frictionless table, starts falling. The problem is to find the speed of the center of mass as a function of position.
The key lies in realizing that since there are no horizontal forces, the center of mass must fall straight down. Since we must find velocity as a function of position, it is natural to apply energy methods.
The sketch shows the stick after it has rotated through angle θ and the center of mass has fallen distance y. The total energy at rest is E = K0 + U0 = Mgl/2
The kinetic energy at a later time isand the corresponding potential energy is
Since, there are no dissipative forces, mechanical energy is conserved and
Hence,
We can eliminate θ by turning to the constraint equation. From the sketch we see thatwe obtain
Torque
The torque 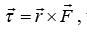 where
where 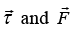 are always perpendicular. There can be a torque on a system with zero net force, and there can be force with zero net torque. In general, there will be both torque and force. These three cases are illustrated in the sketches as shown below. (The torques are evaluated about the centers of the disks.)
are always perpendicular. There can be a torque on a system with zero net force, and there can be force with zero net torque. In general, there will be both torque and force. These three cases are illustrated in the sketches as shown below. (The torques are evaluated about the centers of the disks.)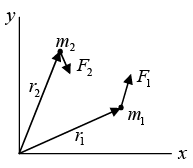

If 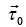 is the component of the torque about the center of mass and
is the component of the torque about the center of mass and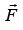 is the total applied force, then torque is given by
is the total applied force, then torque is given by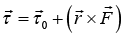
The first term is the torque about the center of mass due to the various external forces, and the second term is the torque due to the total external force acting at the center of mass.
Conservation of Angular Momentum
Torque is important because it is intimately related to the rate of change of angular momentum: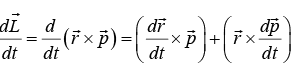
But 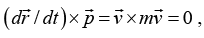 since the cross product of two parallel vectors is zero. Also,
since the cross product of two parallel vectors is zero. Also, 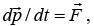 by Newton’s second law. Hence, the second terms is
by Newton’s second law. Hence, the second terms is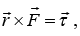 and we have
and we have  If external torque is zero
If external torque is zero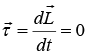 then angular momentum,
then angular momentum,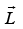 is constant and the angular momentum is conserved.
is constant and the angular momentum is conserved.
Example 6: A disk of mass M and radius b is pulled with constant force F by a thin tape wound around its circumference. The disk slides on ice without friction.
(a) What will be torque about Center of mass
(b) What will be torque about Point A
(c) If Icm is moment of inertia about center of mass. Find the acceleration of center of mass from result obtain by a)
(d) Find the acceleration of center of mass from result (a)
where
and
because
as center of mass is origin
(b) Choose a coordinate system whose origin A is along the line of F . The torque about center of mass C is,
(c) τcm = Icmα ⇒ bF = Icmα ⇒ α = bF/Icm
(d) The torque about A is zero. As we expect that angular momentum about the origin is conserved.
The angular momentum about A is Lz = Icmω + ( R × MV)z = Icmω -bMV.
Since, dLz/dt = 0, we have 0= Icmα - bMα or α =as before.
Example 7: A uniform rod of mass and length a lies on smooth horizontal plane. A particle of mass m moving at speed v0 perpendicular to length of rod strikes it at a distance 4 a from the center and stops after the collision.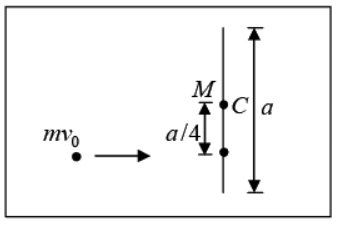
(a) Find the velocity of center of mass of rod
(b) Find the angular velocity of rod about its center of mass just after collision.
From conservation of linear momentum mv0 + M × 0 = m ×0 + Mvcm
System before collision
System after collisionIn this problem Angular momentum is conserve about any point because external torque is zero so from conservation of angular momentum about center of mass
about origin
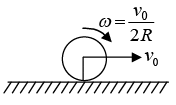
Example 8: A sphere of mass M and radius R having velocity of center of mass v0 and angular velocity V0/2R. The friction of surface are enough that after some time sphere achieve the case of rolling without slipping. Find the velocity of center of mass.
In this problem, the angular momentum is conserved about point of contact P . Initial angular momentum is
The angular momentum about point P when sphere achieve the condition of rolling without slipping
From conservation of angular momentum
Newton’s Law of Motion for Rigid Body
A rigid body having mass M and moment of inertia about center of mass is Icm
External Force 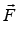 is acting on center of mass and
is acting on center of mass and 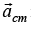 is linear acceleration of center of mass.
is linear acceleration of center of mass.
From Newton’s law of motion, 
Torque about center of mass is 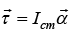 whereis
whereis 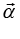 angular acceleration about center of mass
angular acceleration about center of mass
For rolling without slipping, α = αcm/R
Direction of frictional force in case of rotational dynamics
Assume a sphere of mass M and radius R are rolling on a rough surface, where α is acceleration of center of mass and α is angular acceleration.
Case 1: If acceleration of center of mass α is more than Rα , then friction will opposite to direction of acceleration of center of mass F Case 2: If acceleration of center of mass α is less than Rα, then friction will same to direction of acceleration of center of mass
Case 2: If acceleration of center of mass α is less than Rα, then friction will same to direction of acceleration of center of mass
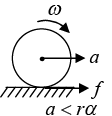 Case 3: In case of rolling without slipping point of contact A will remain at rest, then the direction of frictional force depends on applied torque and possible relative velocity between surface and sphere.
Case 3: In case of rolling without slipping point of contact A will remain at rest, then the direction of frictional force depends on applied torque and possible relative velocity between surface and sphere.
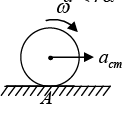
For example if applied force F is at topmost point of sphere then due to torque lowest point will move clock wise direction then frictional force is in same direction of F.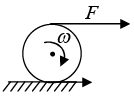 In another example, if sphere is rolling up on inclined plane and by force F and sphere is rolling upward so point of contact A is tend to move clockwise direction to keep this point rest frictional force will in upward direction.
In another example, if sphere is rolling up on inclined plane and by force F and sphere is rolling upward so point of contact A is tend to move clockwise direction to keep this point rest frictional force will in upward direction.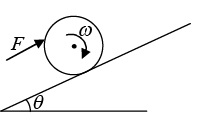
Example 9: A uniform drum of radius R and mass M rolls without slipping down a plane inclined at angle θ. Find its acceleration along the plane. The moment of inertia of the drum about its axis is I0 = MR2/2.
The forces acting on the drum are shown in the diagram. f is the force of friction. The translation of the center of mass along the plane is given by
W sin θ - f = Mα
and the rotation about the center of mass by torque equation Rf = I0α.For rolling without slipping, we also have
α = Rα.
If we eliminate f , we obtain W sin θ - I0 α/b = Mα
Usingwe obtain
Mg sin θ - Mα/2 = Mα or α = 2/3 g sin θ
Example 10: A sphere of mass M and radius R rolling down the wedge with angle θ. Find the minimum value of coefficient of static friction to support pure rolling.
Force equation Mg sin θ - f = Mα ....(i)
The torque equation is given by τ = Icmα
For limiting case μsN ≥ f ⇒ μs.Mg cos θ = 2/7 mg sin θ ⇒ μs ≥ 2/7 tan θ
Example 11: A wheel of radius R and weight W is to be raised over an obstacle of height h by a horizontal force F applied to the centre as shown in figure. Find the minimum value of F.
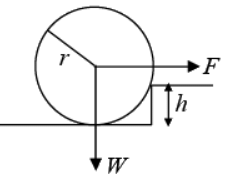
Taking torque about D, the corner of the obstacle,
F × CD = W × BD
Example 12: A force F acts tangentially at the highest point of a sphere of mass M and radius R kept on a rough horizontal plane. If the sphere rolls without slipping, find the acceleration of center of sphere.
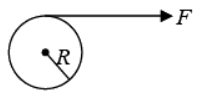
f is frictional force on the lowest point P The force equation is equivalent to
F + f = Ma ....(i)
The torque equation is equivalent to FR - fR = Icmα
For case of rolling without slipping
So torque equation can be reduce to F - f = 2/5 Mα .....(ii)
So solving equation (i) and (ii) we will get 2F = 7/5 Mα ⇒ α = 10F/7M
Example 13: A thin mass less rod of length 2 l has equal point masses m attached at its ends (see figure). The rod is rotating about an axis passing through its centre and making angle θ with it.
(a) Find the angular momentum of system
(b) Find the magnitude of the rate of change of its angular momentum i.e.,
All component of product of inertia is zero,x L = 2ml2ω2sinθcosθ ml2ω2 sin2 θ
Example 14: The linear mass density of a rod of length L varies from one end to the other as 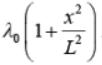 , where x is the distance from one end with tensions T1 and T2 in them (see figure), and λ0 is a constant. The rod is suspended from a ceiling by two massless strings.
, where x is the distance from one end with tensions T1 and T2 in them (see figure), and λ0 is a constant. The rod is suspended from a ceiling by two massless strings.
(a) Find mass of Rod
(b) Find center of mass of Rod
(c) Find tension T1 and T2
(a) The mass of rod is
(b) The centre of gravity of the rod is located at
(c) Force equation T1 + T2 = 4λ0Lg/3
System is in equilibrium about center of mass so
From torque equation
By putting value of T2 = 9/7 T1 in equation, we get T1 + T2 = 4λ0Lg/3and
|
61 videos|23 docs|25 tests
|
FAQs on Rotational Dynamics - Mechanics & General Properties of Matter - Physics
| 1. What is angular momentum and how is it related to particle torque? |  |
| 2. What is Newton's Law of Motion for a rigid body and how does it apply to rotational dynamics? |  |
| 3. What are some applications of rotational dynamics in real-life scenarios? |  |
| 4. How can angular momentum be conserved in a system? |  |
| 5. How is the concept of angular momentum applied in the study of rotational dynamics in the context of IIT JAM? |  |