Q.1. Prove that areal velocity is constant when force is central.
Ans:
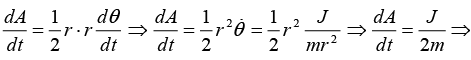 Areal velocity is constant.
Areal velocity is constant.
Q.2. Consider a comet of mass m moving in a parabolic orbit around the Sun. the closest distance between the comet and the Sun is b, the mass of the Sun is M and the universal gravitation constant is G. Then what is angular momentum of the comet.
Ans: l/r = 1 + e cos θ for parabolic orbit e = 1.
For perihelion distance r = rP = b and l/b = 2.
∵ cos θ = 1, l = J2/mk ⇒ J2/mk = 2b ∵ l = 2b
J2 = 2mbk ⇒ J = m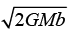 ∵ k = GmM
∵ k = GmM
Q.3. Consider that the motion of a particle of mass m in the potential field
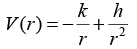 if l is angular momentum.
if l is angular momentum.
(a) Prove that equation is orbit for given potential is same as Kepler’s potential given by
V(r) = - k/r
(b) What is condition that motion is stable and unstable?
Ans:



If 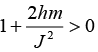 then orbit is bounded and solution can be y = A cos
then orbit is bounded and solution can be y = A cos
and if 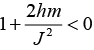 then motion is unbounded y = A cos
then motion is unbounded y = A cos
Q.4. Given L, find the V(r) that leads to a spiral path of the form r = r0eαθ. Choose E to be zero. Hint: Obtain an expression for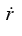 that contains no θ's and then use equation
that contains no θ's and then use equation

Ans: The given information r = r0eαθ yields (using 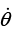 = L / mr2)
= L / mr2)

Plugging into equation, 
this gives, 
Therefore, V(r) = 
Q.5. If a particle of mass m is bounded by potential V (r) = kr moves in a circular orbit with angular frequency ωo. If particle is slightly disturbed with circular orbit what will be frequency of small oscillation.
Ans:(a)
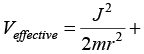 kr, For circular motion
kr, For circular motion

If particle is slightly perturbed from circular orbit then angular frequency is


Q.6. Two particles of identical mass move in circular orbits under a central potential V (r) = 1/2 kr2. Let l1 and l2 be the angular momentum and r1, r2 be the radii of the orbits respectively. If l1/l2, then find the value of r1/r2 is.
Ans:
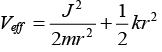 where J is angular momentum.
where J is angular momentum.
Condition for circular orbit 
Thus, 
Q.7. There are three planets in circular orbits around a star at distances α,4α and 9α, respectively. At time t = t0, the star and the three planets are in a straight line. The period of revolution of the closest planet is T. How long after t0 will they again be in the same straight line?
Ans: T1 = ka3/2 = T, T2 = k(4α)3/2 = 8T, T3 = K(9α)3/2 = 27T
Common time that all three star will meet again is t0 = T1 x T2 x T3 = 216T, which is LCM of all time period.
Q.8. A uniform distribution of dust in the solar system adds to the gravitational attraction of the Sun on a planet an additional force
F = -mCr
where m is the mass of the planet, C is a constant proportional to the gravitational constant and the density of the dust, and r is the radius vector from the Sun to the planet (both considered as points). This additional force is very small compared to the direct Sun-planet gravitational force.
(a) Calculate the period for a circular orbit of radius r0 of the planet in this combined field.
(b) Calculate the period of radial oscillations for slight disturbances from the circular orbit.
Ans:
Force due to dust particle F = 

For circular motion 


For circular motion ω0 = 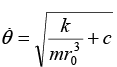 (angular velocity)
(angular velocity)
(b) For small oscillation ω = 


Q.9. A binary star system consists of two stars S1 and S2, with masses m and 2m respectively separated by a distance r. If both S1 and S2 individually follow circular orbits around the centre of mass with instantaneous speeds v1 and v2 respectively, then what is speeds ratio v1/v2.
Ans: Distance between the stars m1 and m2 is r so external force between them is 
Let us assume r1 and r2 be the radius of circular orbit for m1 and m2 respectively.
So from equation of motion 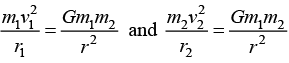

Hence center of circle is at center of mass then m1r1 = m2r2

Q.10. The probe Mangalyaan was sent recently to explore the planet Mars. The inter-planetary part of the trajectory is approximately a half-ellipse with the Earth (at the time of launch), Sun and Mars (at the time the probe reaches the destination) forming the major axis. Assuming that the orbits of Earth and Mars are approximately circular with radii RE and RM, respectively, Find the speed (with respect to the Sun) of the probe during its voyage when it is at a distance r(RE << r << RM) from the Sun, neglecting the effect of Earth and Mars.
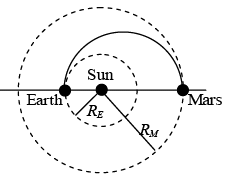 Ans: Total energy E = -K/2a where 2a major axis and 2a = RE+ RM.
Ans: Total energy E = -K/2a where 2a major axis and 2a = RE+ RM.

Q.11. A particle of mass m moves in a potential given by V(r) = βrk . Let the angular momentum be L.
(a) Find the radius r0 of the circular orbit
(b) If the particle is given a tiny kick so that the radius oscillates around r0, find the frequency, ωr of these small oscillations in r
(c) What is the ratio of the frequency ωr to the frequency of the (nearly) circular motion, ωθ ≡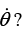 Give a few values of k for which the ratio is rational, that is, for which the path of the nearly circular motion closes back on itself.
Give a few values of k for which the ratio is rational, that is, for which the path of the nearly circular motion closes back on itself.
Ans: (a) for potential V(r) = βrk . A circular orbit exists at the value of r for which the derivative of the effective potential (which is the negative of the effective force) is zero. This is simply the statement that the right-hand side of equation 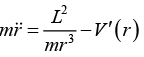 equals zero, so that
equals zero, so that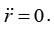 Since V'(r) = βrk-1,the equation gives
Since V'(r) = βrk-1,the equation gives
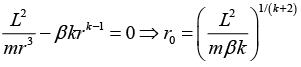 ...(i)
...(i)
If k is negative, then β must also be negative if there is to be a real solution for r0.
(b)
If you work through the r ≡ r0 + ∈ method described above, you will find that you are basically calculating the second derivative of Veff, but in a rather cumbersome way. Using the form of the effective potential, we have

Using the r0 from equation (i) this simplifies to

We could get rid of the r0 here by using equation (i), but this form of ωr will be more useful in part (c).
Note that we must have k >-2 for ωr to be real. If k <-2 , then V''ef (r0) < 0 , which means that we have a local maximum of Veff , instead of a local minimum. In other words, the circular orbit is unstable. Small perturbations grow, instead of oscillating around zero.
(c) for circular orbit ωc = 
But we can also write angular frequency in term of angular momentum Since L = 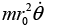 for the circular orbit, we have
for the circular orbit, we have 
Combining this with equation

we find 

A few values of k that yields rational values for this ratio are (the plots of the orbits are shown in figure above): k = -1 ⇒ ωr/ωθ = 1:
This is the gravitational potential. The variable r makes one oscillation for each complete revolution of the (nearly) circular orbit.
k = -2 ⇒ ωr/ωθ = 2:
This is the spring potential. The variable r makes two oscillations for each complete revolution. There is an infinite number of k values that yield closed orbits. But note that this statement applies only to orbits that are nearly circular. Also, the ''closed'' nature of the orbits is only approximate, because it is based on equation 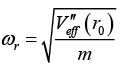 which is an approximate result based on small oscillations. The only k values that lead to exactly closed orbits for any initial conditions are k =-1 (gravity) and k = 2 (spring), and in both case the orbits are ellipses. This result is known as Bertrand's theorem.
which is an approximate result based on small oscillations. The only k values that lead to exactly closed orbits for any initial conditions are k =-1 (gravity) and k = 2 (spring), and in both case the orbits are ellipses. This result is known as Bertrand's theorem.
Q.12. A binary system consists of two stars of equal mass m orbiting each other in a circular orbit under the influence of gravitational forces. The period of the orbit is τ. At t = 0, the motion is stopped and the stars are allowed to fall towards each other. After what time t, expressed in terms of τ, do they collide?
Ans:


when x = R , v = 0 , then c = - A/R

Put x = u2 ⇒ dx = 2udu and x = 0, u = 0 and also, x = R, u = √R


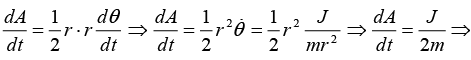 Areal velocity is constant.
Areal velocity is constant.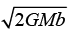 ∵ k = GmM
∵ k = GmM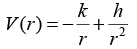 if l is angular momentum.
if l is angular momentum.


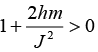 then orbit is bounded and solution can be y = A cos
then orbit is bounded and solution can be y = A cos
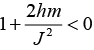 then motion is unbounded y = A cos
then motion is unbounded y = A cos
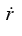 that contains no θ's and then use equation
that contains no θ's and then use equation
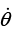 = L / mr2)
= L / mr2)



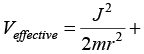 kr, For circular motion
kr, For circular motion



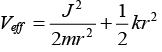 where J is angular momentum.
where J is angular momentum.






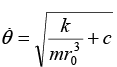 (angular velocity)
(angular velocity)



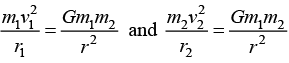


 Ans: Total energy E = -K/2a where 2a major axis and 2a = RE+ RM.
Ans: Total energy E = -K/2a where 2a major axis and 2a = RE+ RM.
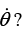 Give a few values of k for which the ratio is rational, that is, for which the path of the nearly circular motion closes back on itself.
Give a few values of k for which the ratio is rational, that is, for which the path of the nearly circular motion closes back on itself.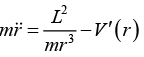 equals zero, so that
equals zero, so that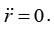 Since V'(r) = βrk-1,the equation gives
Since V'(r) = βrk-1,the equation gives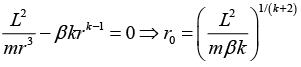 ...(i)
...(i)



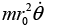 for the circular orbit, we have
for the circular orbit, we have 



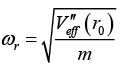 which is an approximate result based on small oscillations. The only k values that lead to exactly closed orbits for any initial conditions are k =-1 (gravity) and k = 2 (spring), and in both case the orbits are ellipses. This result is known as Bertrand's theorem.
which is an approximate result based on small oscillations. The only k values that lead to exactly closed orbits for any initial conditions are k =-1 (gravity) and k = 2 (spring), and in both case the orbits are ellipses. This result is known as Bertrand's theorem.

























