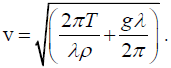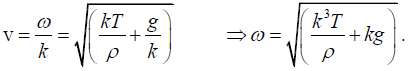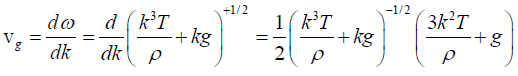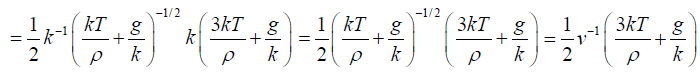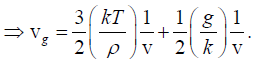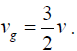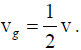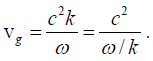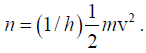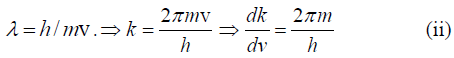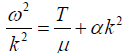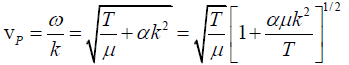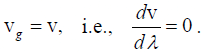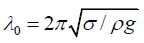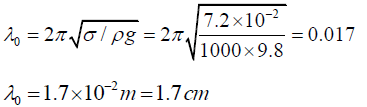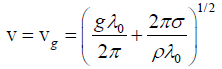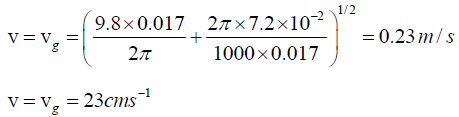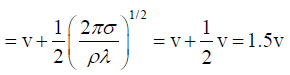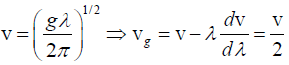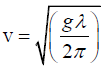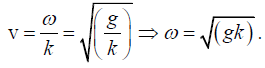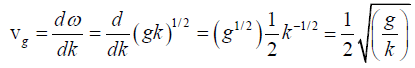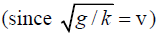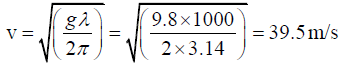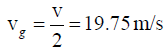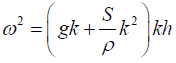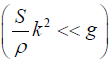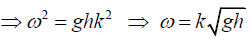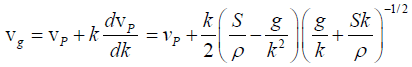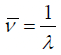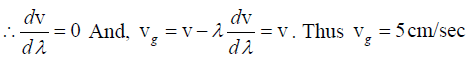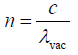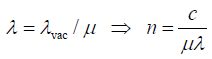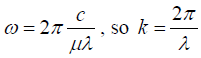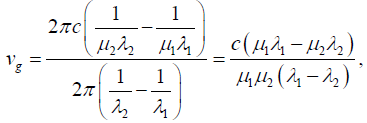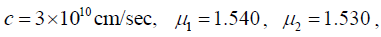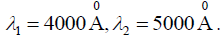Phase & Group Velocity: Assignment | Oscillations, Waves & Optics - Physics PDF Download
Q.1. The phase velocity of surface waves of wavelength λ on a liquid of density ρ and surface tension T is given by, 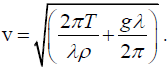 Find the group velocity.
Find the group velocity.
The phase velocity on water surface is controlled mainly by surface tension and is
given by
Since, 2π/λ = k, where k is propagation constant.
Then the wave velocity,
The group velocity,
This is the expression for the group velocity vg in terms of the wave velocity v.
We can see that if we neglect the effect of gravity (g =0) then
If we neglect the effect of surface tension (T =0), then
Q.2. If the angular velocity ω and the propagation number k of a wave are related by
ω2 = c2k2 +ω20, where c and ω0 are constants, then show that the product of group
velocity and phase velocity is a constant.
The given relation is, ω2 = c2k2 +ω20,
Differentiating ω with respect to k, we get
By definition, dω/dk is the group velocity,
Again, by definition, ω/k is the phase velocity v,
Q.3. The dispersion relation for water waves of very short wavelength in deep water is 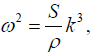 where S is the surface tension and ρ is the density.
where S is the surface tension and ρ is the density.
(a) What is the phase velocity of these waves?
(b) What is the group velocity?
(c) Is the group velocity greater or less than phase velocity?
Q.4. A wave packet of mean wavelength 3.6 x 10 cm is traveling with phase velocity 1.8 x 1010 cm/sec in a dispersive medium of carbon-di-sulphide. From the dispersion of the medium, dv/dλ is computed to be 3.8x1013 per sec . Calculate the group velocity in carbon-di-sulphide.
The group velocity vg is related to the phase velocity by
vg = (1.8 x 1010 cm/sec) - (3.6 x 10-5 cm) (3.8 x 1013 /sec)
= (1.8 x 1010 cm/sec) - (13.68 x 108 cm/sec) = (1.8x1010 cm/sec ) - (0.1368 x 1010 cm/sec).
= 1.66 x 1010 cm/sec.
Q.5. If the frequency of matter wave is 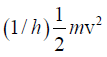 and the wavelength is h/mv , show that the group velocity is v.
and the wavelength is h/mv , show that the group velocity is v.
The angular frequency is ω =2πn.
Here the wave frequency is....(i)
Again, the propagation constant, k = 2π/λ
For matter wave,
Dividing equation (i) and (ii), we have dω/dk = v.
By definition, dω/dk is the group velocity vg, ∴ vg = v.
Q.6. It is only when a string is perfectly flexible that the phase velocity of a wave on a string is given by 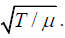 The dispersion relations for the real piano wire can be written as
The dispersion relations for the real piano wire can be written as 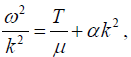 where α is a small positive quantity which depends on the stiffness of the string. For perfectly flexible string, α = 0. Obtain expressions for phase velocity vp and group velocity vg and show that vp increases as wavelength decrease.
where α is a small positive quantity which depends on the stiffness of the string. For perfectly flexible string, α = 0. Obtain expressions for phase velocity vp and group velocity vg and show that vp increases as wavelength decrease.
The dispersion relation is given as,
The phase velocity,(for small α)
Since k = 2π/λ, vp increase as λ decrease.
The group velocity is given by,
Q.7. The phase velocity of deep-water waves is given by, 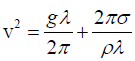 . Where, g = 9.8ms-2 ,ρ = 1000kgm-3 and σ= 7.2 x 10-2 Nm (σ is the Surface tension of water).
. Where, g = 9.8ms-2 ,ρ = 1000kgm-3 and σ= 7.2 x 10-2 Nm (σ is the Surface tension of water).
(a) Determine the value (λ0) of the wavelength of the waves which do not disperse in water. What is the phase and group velocities at this wavelength?
(b) Show that for wavelength λ <<λ0; vg = 1.5v and λ>>λ0; vg = v/2
(a). For no dispersion,
Differentiating the expressionwith respect to λ and setting
and λ = λ0 gives
Substituting the values of g, σ, ρ and λ0 yields,Thus, waves of average wavelength of 1.7cm do not disperse in water. The group and
phase velocities at λ0 are equal to each other.
Substituting the values of g, σ, ρ and λ0 yields,
(b) For λ<<λ0 the surface tension term dominates, so that
Now,
This is the speed with which ripples (short-wavelength waves) propagate in water. Forsuch waves vg > v, indicating that they show anomalous dispersion.
And if λ>>λ0 the gravity term dominates. The phase velocity of these long wavelength waves is, therefore, given by
These waves show normal dispersion, i.e., their phase velocity decrease with decrease in wavelength.
Q.8. Neglecting the effects of surface tension and finite depth, the wave velocity of water wave of wavelength λ is given by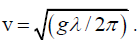 Prove that the group velocity is half the wave velocity. Calculate group velocity and wave velocity for λ = 1000m.
Prove that the group velocity is half the wave velocity. Calculate group velocity and wave velocity for λ = 1000m.
The phase velocity of wave in deep water (gravity waves) is given by,
Since 2π/λ = k, where k is propagation constant
Then the phase velocity or wave velocity is
The group velocity,
Hence, vg = 1/2 v
Therefore, the wave velocity for λ = 1000m is,
And the group velocity is
Thus, the gravity waves are highly dispersive. The individual waves travel much morerapidly within the group.
Q.9. The general dispersion relation for water waves can be written as

Where g is acceleration due to gravity, ρ is the density of water, S is the surface
tension and h is the water depth. Use the properties of tan hx function viz.
For x >>1, tan hx =1 and for x<<1, tan hx = x. Show that
(a) in shallow water the group velocity and the phase velocity are both equal to 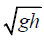 if the wavelength is long enough to ensure that
if the wavelength is long enough to ensure that 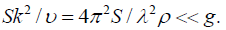
(b) Show that for deep water the phase velocity is given by 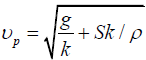 and find the group velocity.
and find the group velocity.
If kh <<1, then tanh(kh) = kh, then
If the second term in the bracket is smaller than the first one i.e.,
then,and group velocity
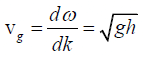
∴ vg = vp
(b) kh >>1, tanh(kh) = 1 then
phase velocity,
Group velocity,
And,For short wavelengths k is larger, the first term in both the numerator and denominator will be smaller and vg = 3/2vp, while for long wavelength k is small and vg = 1/2vp.
Q.10. (i) Calculate the wave number for gamma rays of wavelength 1A0.
(ii) The angular frequency is five times of the propagation constant. Calculate phase and group velocities.
(i) The wave number
(say) is defined by
Given that,
(ii) The angular frequency ω is 5 times the propagation constant, that is, ω/k = 5
where ω/k is the phase velocity v . Thus v = 5cm/ sec
if k is per cm. here ω/k is constant, that is v = constant
Q.11. The refractive indices of a medium for two spectral lines of wavelength 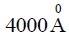 and
and 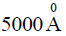 are 1.540 and 1.530 respectively. Calculate the value of the group velocity. Velocity of light in vacuum is 3 x 1010 cm/sec.
are 1.540 and 1.530 respectively. Calculate the value of the group velocity. Velocity of light in vacuum is 3 x 1010 cm/sec.
The group velocity,
...(1)
Where, ω is angular frequency and k is propagation constant
Now, ω = 2πn, where n is frequency, which is given by,Where λvac is the wavelength of light in vacuum. If λ be the wavelength in a medium of
refractive index μ, then
thus
From equation (i), we have,
Given:
|
54 videos|22 docs|14 tests
|
FAQs on Phase & Group Velocity: Assignment - Oscillations, Waves & Optics - Physics
| 1. What is phase velocity? |  |
| 2. What is group velocity? |  |
| 3. How are phase velocity and group velocity related? |  |
| 4. What is the significance of phase and group velocities? |  |
| 5. How do phase and group velocities differ in different media? |  |