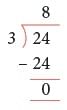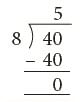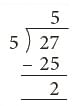Division Class 2 Notes Maths
| Table of contents |

|
| What is Division? |

|
| Division as Repeated Subtraction |

|
| Relation between Multiplication and Division |

|
| Properties of Division |

|
| Problems Based on Real Life Situations |

|
What is Division?
Division means the act of sharing or grouping things equally.
Equal Sharing
1. Mamta wants to share 4 chocolates between 2 of her friends Sonu and Bunty. How many chocolates will each of them get?
Ans: To determine how many chocolates Sonu and Bunty will each receive, we divide the total number of chocolates by the number of friends: Mamta starts with 4 chocolates.
She distributes them equally between 2 friends.
Using division: 4 ÷ 2 = 2.
Therefore, each friend receives 2 chocolates.
2. Mohit has 10 packets of chips. He wants to share them equally with his cousin. How many packets will each one of them get?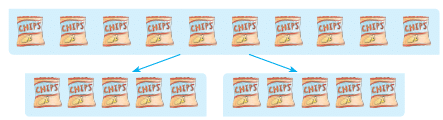
Ans: Clearly, each one of them will now have 5 packets of chips.
We say that 10 divided by 2 is 5 and write 10 ÷ 2 = 5.
Equal Grouping
Let us divide 12 balloons into three equal groups. How many balloons will each group contain?
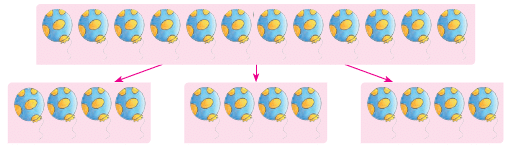
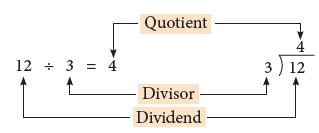
Ans: When we divide 12 balloons into three equal groups, each group will contain 4 balloons. We calculate this using the division fact 12 ÷ 3 = 4. In this calculation:
The number being divided, 12, is called the dividend.
The number by which we are dividing, 3, is called the divisor.
The result of the division, 4, is called the quotient.
Note: ‘÷’ is the symbol of division.
Thus, we can say that division means dividing or separating into equal groups.
Division as Repeated Subtraction
We know that multiplication is repeated addition. Similarly, division is repeated subtraction.
Sidhu was ill. The doctor gave him 12 tablets. For how many days did the medicine last if he had to take 2 tablets daily?
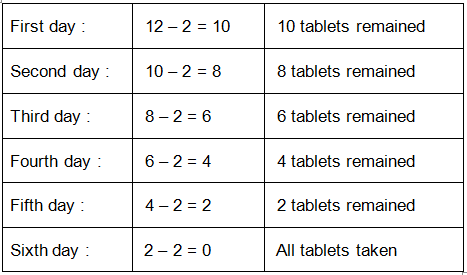
Last 2 tablets were taken on the sixth day. The medicine lasted 6 days. Here, 2 has been subtracted 6 times.
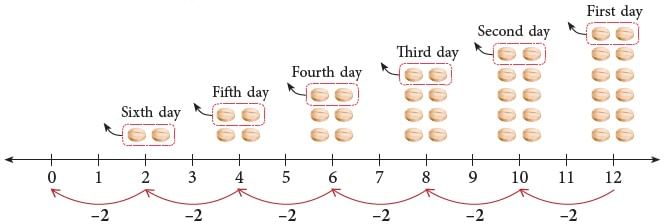
The above repeated subtraction sentence
12 – 2 – 2 – 2 – 2 – 2 – 2 = 0
can be written in the division form as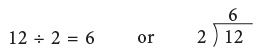
Division as Repeated Subtraction on the Number Line
How many times can you subtract 5 from 25?

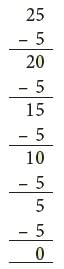
Start at 25. Jump backwards to the left 5 steps at a time in one jump till you reach 0.
The number of jumps is 5.
25 ÷ 5 = 5.
So, you can subtract 5 five times from 25.
Relation between Multiplication and Division
The picture shows 12 balls arranged in groups of 4.

It shows a multiplication fact: 3 × 4 = 12 and a division fact: 12 ÷ 4 = 3.
12 balls can also be arranged in groups of 3 as shown.
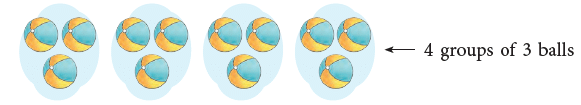
It shows a multiplication fact: 4 × 3 = 12 and a division fact: 12 ÷ 3 = 4.
Thus, we observe that the
- multiplication fact 3 × 4 = 12 gives the division fact 12 ÷ 4 = 3.
- multiplication fact 4 × 3 = 12 gives the division fact 12 ÷ 3 = 4.
By the order property of multiplication we know that, 3 × 4 = 4 × 3 = 12.
So, the multiplication fact, 3 × 4 = 12 or 4 × 3 = 12, gives two related division facts, 12 ÷ 4 = 3 and 12 ÷ 3 = 4.
A few examples are given below.
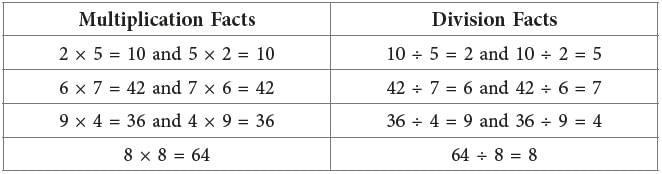
From the above examples, we see that multiplication and division are inverse operations.
For every multiplication fact, with two different factors, there can be two division facts and vice-versa. However, a multiplication fact of same number gives only one division fact.
Example: 5 × 5 = 25 gives 25 ÷ 5 = 5.
Division using Multiplication Tables
Let us find 18 ÷ 6.
Recite the multiplication table of 6 till you reach 18.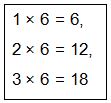
Since 3 times 6 is 18, so, 18 ÷ 6 = 3.
Similarly, to find 32 ÷ 8, recite the table of 8 till you reach 32.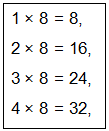
Since 4 times 8 is 32, so, 32 ÷ 8 = 4.
Terms Related to Division
In a division sum,
- the number to be divided is called the dividend.
- the number by which we divide is called the divisor.
- the answer we get after division is called the quotient.
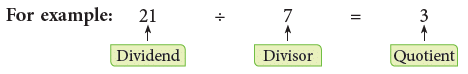
Properties of Division
1. Division of a number by itself
Three bananas are distributed equally among 3 girls. How many bananas does each girl get?
Each girl gets 1 banana. So, 3 ÷ 3 = 1.
Any number divided by itself gives 1 as the answer.
2. Division of a number by 1
There are 5 laddoos in a plate. When all the 5 laddoos are given to 1 child, there are no laddoos left.
This gives 5 ÷ 1 = 5.
3. Division of 0 by any number
Zero divided by any number except 0 is zero.
Examples: 0 ÷ 7 = 0, 0 ÷ 8 = 0.
If 0 objects are distributed among any number of children, each child gets nothing.
Long Division Method
Example 1: Divide 24 by 3.
Step 1. Arrange the numbers as
that is,
Step 2. Recite the table of 3 till you reach 24.
1 × 3 = 3, 2 × 3 = 6, 3 × 3 = 9, 4 × 3 = 12,
5 × 3 = 15, 6 × 3 = 18, 7 × 3 = 21, 8 × 3 = 24
Step 3. Stop at 24 and write 8 as the quotient.
Step 4. Write 24 below 24 and subtract.
Thus, 24 ÷ 3 = 8.
Division with Remainder
Look at the following examples
There are 7 notebooks and 3 girls. Each girl gets 2 notebooks when divided equally and 1 notebook remains.
7 = 3 times 2 and 1
Now, suppose there are 13 apples and 6 boys. How many apples does each boy get when divided equally? How many apples remain?
13 = 6 times 2 and 1
Each boy gets 2 apples and 1 apple remains.
When 13 is divided by 6, the quotient is 2 and the remainder is 1.
We write the result as
Problems Based on Real Life Situations
Example: 40 pencils are to be packed equally in 8 boxes. How many pencils
will be there in each box?
Total number of pencils = 40
Number of boxes = 8
Each box has (40 ÷ 8) pencils = 5 pencils.
Example: Annie wants to put 27 flowers equally in 5 vases. She keeps the remaining flowers with herself. How many flowers did she keep with herself?
Total number of flowers = 27
Number of vases = 5
Each vase has (27 ÷ 5) flowers = 5 flowers and 2 remain
Each vase has 5 flowers and 2 flowers remain with Annie.
|
34 videos|104 docs|84 tests
|
FAQs on Division Class 2 Notes Maths
| 1. What is division? |  |
| 2. How is division related to repeated subtraction? |  |
| 3. Can you give an example of division as repeated subtraction? |  |
| 4. What happens if the dividend is not divisible by the divisor in division? |  |
| 5. Are there any special rules or properties of division? |  |