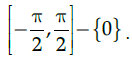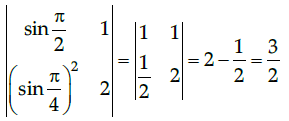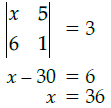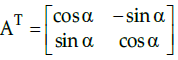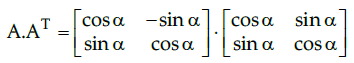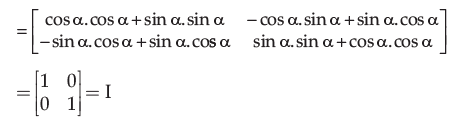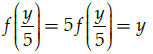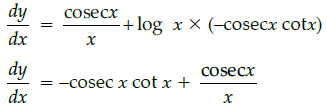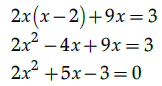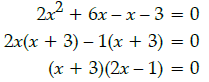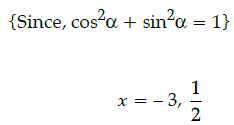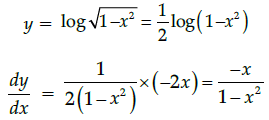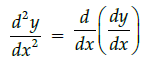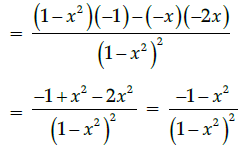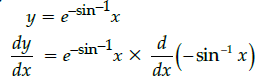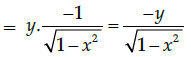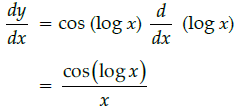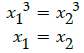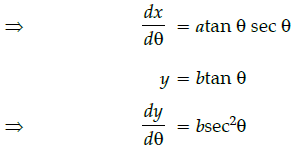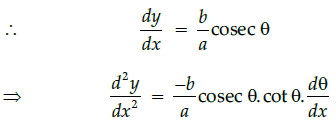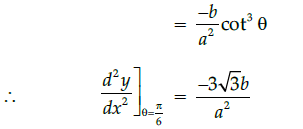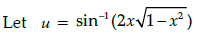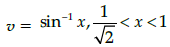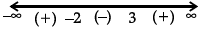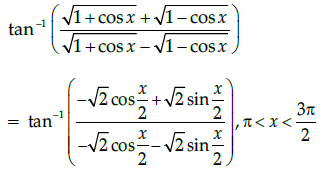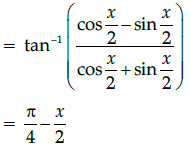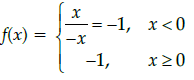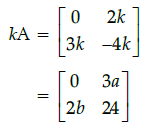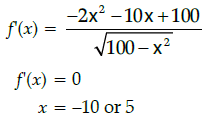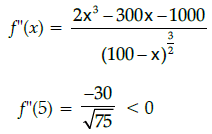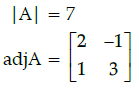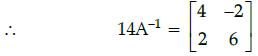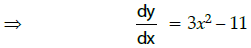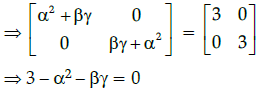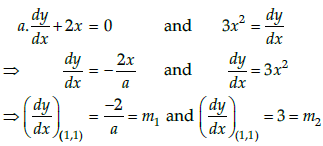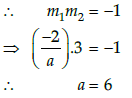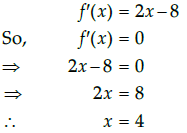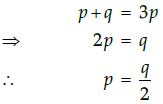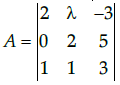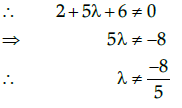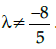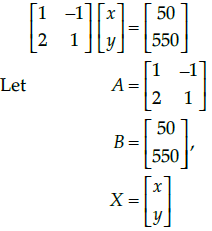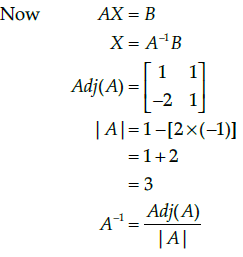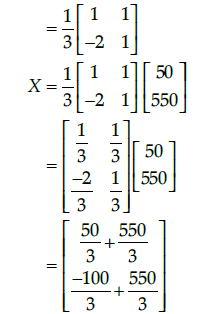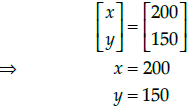Class 12 Mathematics: CBSE Sample Question Paper- Term I (2021-22)- 2 | Mathematics (Maths) Class 12 - JEE PDF Download
| Table of contents |

|
| Class-XII |

|
| Time: 90 Minutes |

|
| Max. Marks: 40 |

|
| Section - A |

|
| Section - B |

|
| Section - C |

|
Class-XII
Time: 90 Minutes
Max. Marks: 40
General Instructions :
- This question paper contains three sections – A, B and C. Each part is compulsory.
- Section - A has 20 MCQs, attempt any 16 out of 20.
- Section - B has 20 MCQs, attempt any 16 out of 20.
- Section - C has 10 MCQs, attempt any 8 out of 10.
- There is no negative marking.
- All questions carry equal marks
Section - A
Q.1: What is the principal value branch of cosec–1 x ?
(a) (-1, 1)
(b) [-1,1]
(c) 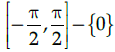
(d) 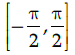
Correct Answer is Option (c)
The cosec function is periodic so to calculate its inverse function we need to make the function bijective. For that we have to consider an interval in which all values of the function exist and do not repeat. For cosec function this interval is considered as
Thus when we take the inverse of the function the domain becomes range and the range becomes domain. Hence the principal value branch is the range of cosec–1 x, that is
Q.2: Find the value of k if derivative of the function exists 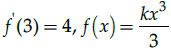
(a) k = 4/5
(b) k = 4/7
(c) k = 4/9
(d) k =4/11
Correct Answer is Option (c)
Differentiate and substitute the given value.
Q.3: The number of all possible matrices of order 3 × 3 with each entry 0 or 1 is:
(a) 9
(b) 28
(c) 512
(d) 64
Correct Answer is Option (c)
The given matrix of the order 3 × 3 has 9 elements and each of these elements can be either 0 or 1. Now, each of the 9 elements can be filled in two possible ways. Therefore, by the multiplication principle, the required number of possible matrices is 29 = 512.
Q.4: Calculate the determinant of the given matrix 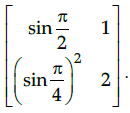
(a) 1/2
(b) -1/2
(c) 3/2
(d) None of the above
Correct Answer is Option (c)
Q.5: Which of the following is satisfied by the function, f (x)= 2 sin x−x+1 in the interval 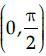
(a) Function has local minimum at x = π/3
(b) Function has local maximum at x = π/3
(c) Function has no critical points in the given interval
(d) Function is increasing in the given interval
Correct Answer is Option (b)
f'(x) > 0 for x < π/3 and f"(x) < 0 for x < π/3
Q.6: if 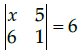 then the value of x is:
then the value of x is:
(a) –6
(b) –36
(c) 6
(d) 36
Correct Answer is Option (d)
Q.7: If the set A contains 3 elements and the set B contains 6 elements, then the number of bijective mappings from A to B is:
(a) 520
(b) 10
(c) 0
(d) None of these
Correct Answer is Option (c)
We know that, if A and B are two non-empty finite sets containing m and n elements, respectively, then the number of one-one and onto mapping (bijective mappings) from A to B is
n! if m = n 0,
if m ≠ n
Given that, m = 5 and n = 6 ⇒ m ≠ n
Number of one-one and onto mapping = 0
Q.8: If 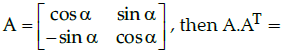
(a) Null Matrix
(b) I
(c) A
(d) –A
Correct Answer is Option (b)
Q.9: The normal to curve y = 7x2 – x4 at x=2 passes through
(a) (30,4)
(b) (20,4)
(c) (10,5)
(d) (5,20)
Correct Answer is Option (b)
Tangent is perpendicular to the normal.
Q.10: What is the domain of the sin–1 x ?
(A) [–∞,∞]
(B) (∞,-∞)
(C) (–1, 1)
(D) [–1, 1]
Correct Answer is Option (d)
The sine function is periodic so to calculate its inverse function we need to make the function bijective. For that we have to consider an interval in which all values of the function exist and do not repeat. Now for the inverse of a function the domain becomes range and the range becomes domain. Thus the range of sine function, that is, [-1,1] becomes the domain of inverse function.
Q.11: Let f : R → R be defined as f (x) = 5x. Choose the correct answer.
(a) f is one-one onto
(b) f is many-one onto
(c) f is one-one but not onto
(d) f is neither one-one nor onto
Correct Answer is Option (a)
f : R → R is defined as f(x) = 5x. Let x, y ∈ R such that
f(x) = f(y) ⇒ 5x = 5y
⇒ x = y
Therefore, f is one-one. Also, for any real number (y) in co-domain R, there exists y/5 in R such that
Therefore, f is onto. Hence, function f is one-one and onto.
Q.12: Find dy/dx where y = cosec x log x.
(a) 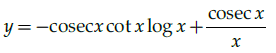
(b) 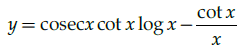
(c) 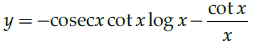
(d) 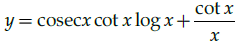
Correct Answer is Option (a)
y = cosecx logx
Q.13: The value of x for the given determinant 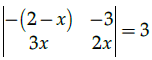 is
is
(a) ± 3
(b) 3, 1/2
(c) 0
(d) -3, 1/2
Correct Answer is Option (d)
In the given determinant, to find the value of x,
Q.14: What is second derivative of the function, 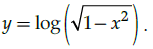
(a) 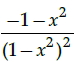
(b) 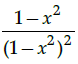
(c) 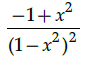
(d) 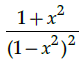
Correct Answer is Option (a)
Q.15: Skew symmetric matrix is also called:
(a) symmetric
(b) identical matrix
(c) square matrix
(d) anti symmetric
Correct Answer is Option (d)
In mathematics, particularly in linear algebra, a skew symmetric (or anti symmetric or antisymmetric) matrix is a square matrix whose transpose equals its negative; that is, it satisfies the condition A = – At.
Q.16: What are the local maximum and minimum for the function 3x4 −54x2 −108x+4x3 in the interval [–5 5]
(a) x =−1, 3,−3
(b) x =−1, 3,−2
(c) x =−1, 4,−4
(d) x = 2, 3,−3
Correct Answer is Option (a)
Max and min points are the points at which derivative has value 0.
Q.17: Matrix 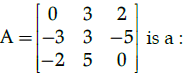
(a) Skew-symmetric matrix
(b) Symmetric matrix
(c) Scalar matrix
(d) None of these
Correct Answer is Option (d)
The given matrix is not a skew symmetric matrix as A’ ≠ -A. By Definition; we know, A matrix is a skew- symmetric matrix if A’ = -A.
Q.18: Find dy/dx where 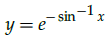
(a) 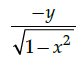
(b) 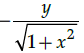
(c) 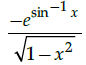
(d) 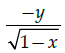
Correct Answer is Option (a)
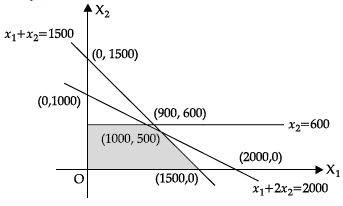
Q.19: For the constraints of a LPP problem given by
x1 + 2x2 ≤ 2000, x1 + x2 ≤ 1500, x2 ≤ 600 and x1, x2 ≥ 0, the points does not lie in the positive bounded region.
(a) (1000,0)
(b) (0, 500)
(c) (2, 0)
(d) (2000,0)
Correct Answer is Option (d)
From the graph, it is clear that the point (2000, 0) is outside.
Q.20: If y = f (x)= sin(log x), then dy/dx =
(a) 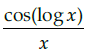
(b) 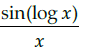
(c) 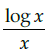
(d) 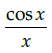
Correct Answer is Option (a)
y = f(x) = sin(log x)
Section - B
Q.21: The function f : R → R defined as f(x) = x3 is:
(a) One-one but not onto
(b) Not one-one but onto
(c) Neither one-one nor onto
(d) One-one and onto
Correct Answer is Option (d)
Let f(x1) = f(x2) ∀ x1, x2 ∈ R
⇒ f is one-one Let f(x) = x3 = y ∀ y ∈ R
⇒ x = y1/3 every image y ∈ R has a unique pre image in R
⇒ f is onto
∴ f is one-one and onto.
Q.22: If x = a sec θ, y = b tan θ, then 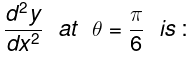
(a) 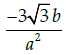
(b) 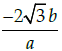
(c) 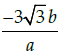
(d) 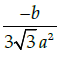
Correct Answer is Option (a)
x = a secθ
Q.23: In the given graph, the feasible region for a LPP is shaded. The objective function Z = 2x – 3y, will be minimum at: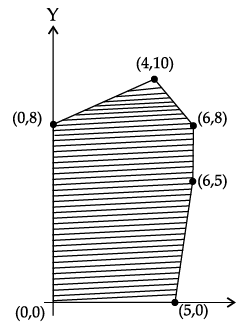
(a) (4, 10)
(b) (6, 8)
(c) (0, 8)
(d) (6, 5)
Correct Answer is Option (c)
Z is minimum –24 at (0, 8)
Q.24: The derivative of 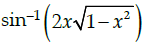 w.r.t
w.r.t 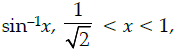 is:
is:
(a) 2
(b) π/2 - 2
(c) π/2
(d) -2
Correct Answer is Option (a)
and
⇒ sin v = x ...(i)Using (i), we get
⇒ sin–1(2sin v cos v)
⇒ u = 2v
Differentiating with respect to v, we get:
du/dv = 2
Q.25: if 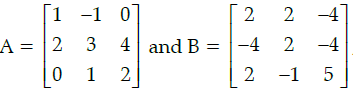 , then:
, then:
(a) A–1 = B
(b) A–1 = 6B
(c) B–1 = B
(d) B–1 = 1/6A
Correct Answer is Option (d)
AB = 6I
B–1 = 1/6A
Q.26: The real function f(x) = 2x3 – 3x2 – 36x + 7 is:
(a) Strictly increasing in (− ∞,−2) and strictly decreasing in ( −2, ∞)
(b) Strictly decreasing in ( −2, 3)
(c) Strictly decreasing in (− ∞, 3) and strictly increasing in (3, ∞)
(d) Strictly decreasing in (− ∞, −2) ∪ (3, ∞)
Correct Answer is Option (b)
f'(x) = 6(x2 – x – 6)
= 6(x – 3)(x + 2)
As f'(x) < 0∀ x ∈ (–2, 3)⇒ f(x) is strictly decreasing in (–2, 3)
Q.27: Simplest form of 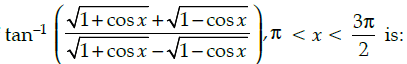
(a) π/2 - x/2
(b) 3π/2 - x/2
(c) -x/2
(d) π - x/2
Correct Answer is Option (a)
Q.28: Given that A is a non-singular matrix of order 3 such that A2 = 2A, then value of |2A| is:
(a) 6
(b) 8
(c) 64
(d) 16
Correct Answer is Option (c)
A2 = 2A
⇒ |A2| = |2A|
⇒ |A|2 = 23|A|
as |kA| = kn|A| for a matrix of order n.⇒ either |A| = 0 or |A| = 8
But A is non-singular matrix
∴ |2A| = 82 = 64
Q.29: The value of b for which the function f(x) = x + cosx + b is strictly decreasing over R is:
(a) b < 1
(b) No value of b exists
(c) b ≤ 1
(d) b ≥ 1
Correct Answer is Option (b)
f'(x) = 1 – sin x
⇒ f'(x) > 0 ∀ x ∈ R
⇒ no value of b exists
Q.30: Let R be the relation in the set N given by R = {(a, b) : a = b – 2, b > 6}, then:
(a) (2, 4) ∈ R
(b) (3, 8) ∈ R
(c) (6, 8) ∈ R
(d) (8, 7) ∈ R
Correct Answer is Option (c)
a = b – 2 and b > 6
⇒ (6, 8) ∈ R
Q.31: The point(s), at which the function f given by 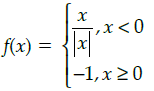 is continuous, is/are:
is continuous, is/are:
(a) −6, −12, −18
(b) −6, −4, −9
(c) −6, 4, 9
(d) −6, 12, 18
Correct Answer is Option (a)
⇒ f(x) = –1∀ x ∈ R
⇒ f(x) is continuous ∀ x ∈ R as it is a constant function
Q.32: If 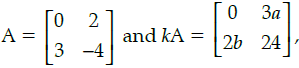 then the values of k, a and b respectively are:
then the values of k, a and b respectively are:
(a) −6, −12, −18
(b) −6, −4, −9
(c) −6, 4, 9
(d) −6, 12, 18
Correct Answer is Option (b)
⇒ k = –6, a = –4
and b = –9
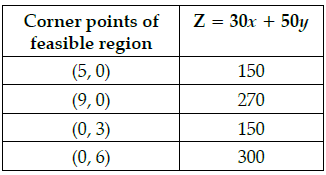
Q.33: A linear programming problem is as follows: Minimize Z = 30x + 50y subject to the constraints,
3x + 5y ≥15
2x + 3y ≤ 18
x ≥ 0, y ≥ 0
In the feasible region, the minimum value of Z occurs at
(a) a unique point
(b) no point
(c) infinitely many points
(d) two points only
Correct Answer is Option (d)
Minimum value of Z occurs at two points
Q.34: The area of a trapezium is defined by function f and given by 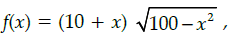 then the area when it is maximised is:
then the area when it is maximised is:
(a) 75 cm2
(b) 7√3 cm2
(c) 75√3 cm2
(d) 5cm2
Correct Answer is Option (c)
But x > 0⇒ x = 5
Maximum area of trapezium is 75√3 cm2 when x = 5
Q.35: If A is square matrix such that A2 = A, then (I + A)³ – 7 A is equal to:
(a) A
(b) I + A
(c) I − A
(d) I
Correct Answer is Option (d)
(I + A)3 – 7A
= I + A + 3A + 3A – 7A = I
Q.36: If tan–1 x = y, then:
(a) −1< y <1
(b) 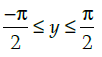
(c) 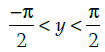
(d) 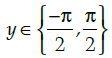
Correct Answer is Option (c)
Q.37: Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. Based on the given information, f is best defined as:
(a) Surjective function
(b) Injective function
(c) Bijective function
(d) function
Correct Answer is Option (b)
As every per-image x ∈A has a unique image y ∈ B
⇒ f is injective function
Q.38: For  then 14A–1 is given by:
then 14A–1 is given by:
(a) 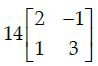
(b) 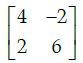
(c) 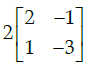
(d) 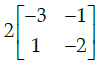
Correct Answer is Option (b)
Q.39: The point(s) on the curve y = x3 – 11x + 5 at which the tangent is y = x – 11 is/are:
(a) (–2, 19)
(b) (2, – 9)
(c) (±2, 19)
(d) (–2, 19) and (2, – 9)
Correct Answer is Option (b)
y = x3 – 11x + 5
Slope of line y = x – 11 is 1⇒ 3x2 – 11 = 1
⇒ x = ± 2
∴ point is (2, –9) as (–2, 19) does not satisfy given line
Q.40: Given that 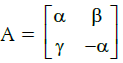 and A2 = 3I, then:
and A2 = 3I, then:
(a) 1 + α2 + βg = 0
(b) 1 – α2 – βg = 0
(c) 3 – α2 – βg = 0
(d) 3 + α2 + βg = 0
Correct Answer is Option (c)
A2 = 3I
 |
Download the notes
Class 12 Mathematics: CBSE Sample Question Paper- Term I (2021-22)- 2
|
Download as PDF |
Section - C
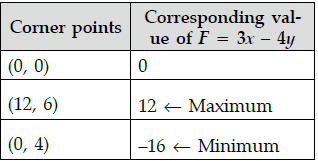
Q.41: The feasible region for an LPP is shown in the given Figure. Let F = 3x – 4y be the objective function. Maximum value of F is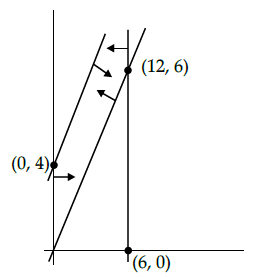
(a) 0
(b) 8
(c) 12
(d) –18
Correct Answer is Option (c)
The feasible region as shown in the figure, has objective function F = 3x – 4y.
Hence, the maximum value of F is 12.
Q.42: If the curve ay + x2 = 7 and x3 = y, cut orthogonally at (1, 1), then the value of a is:
(a) 1
(b) 0
(c) –6
(d) 6
Correct Answer is Option (d)
Given that, ay + x2 = 7 and x3 = y
On differentiating both equations with respect to x, we get
Since, the curve cuts orthogonally at (1, 1).
Q.43: If x is real, the minimum value of x2 – 8x + 17 is
(a) -1
(b) 0
(c) 1
(d) 2
Correct Answer is Option (c)
Let,
f (x) = x2 - 8x + 17
On differentiating with respect to x, we get
Now, Again on differentiating with respect to x, we get
f"(x) = 2 > 0,∀xSo, x = 4 is the point of local minima. Minimum value of f(x) at x = 4
f(4) = 4.4 − 8.4 + 17 = 1
Q.44: Corner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px + qy, where p, q > 0. Condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is
(a) p = 2q
(b) p = q/2
(c) p = 3q
(d) p = q
Correct Answer is Option (b)
So, condition of p and q, so that the minimum of Z occurs at (3, 0) and (1, 1) is
Q.45: if 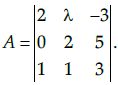 Then A-1 exist if
Then A-1 exist if
(a) λ = 2
(b) λ ≠ 2
(c) λ ≠ –2
(d) None of these
Correct Answer is Option (a)
Given that,
Expanding along R1,
|A| = 2(6-5) - λ(-5) -3(-2)
= 2 + 5λ + 6We know that A-1 exists, if A is nonsingular matrix, i.e., |A|≠0
So, A−1 exists if and only if
Questions 46-50 are based on a Case-Study
Case- Study
Manjit wants to donate a rectangular plot of land for a school in his village. When he was asked to give dimensions of the plot, he told that if its length is decreased by 50 m and breadth is increased by 50 m, then its area will remain same, but if length is decreased by 10 m and breadth is decreased by 20 m, then its area will decrease by 5300 m2. Based on the given information, answer the following questions.

Q.46: The equations in terms of x and y are
(a) x – y = 50, 2x – y = 550
(b) x – y = 50, 2x + y = 550
(c) x + y = 50, 2x + y = 550
(d) x + y = 50, 2x + y = 550
Correct Answer is Option (b)
Let length of the plot be x and breadth be y.
According to question,
xy = (x – 50)(y + 50)
xy = xy + 50x – 50y – 2500
x – y = 50And
(xy – 5300) = (x – 10)(y – 20)
xy – 5300 = xy – 20x – 10y + 2002x + y = 550 ...(ii)
Q.47: Which of the following matrix equation is represented by the given information
(a) 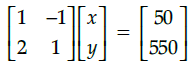
(b) 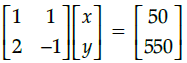
(c) 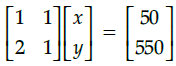
(d) 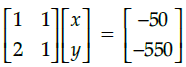
Correct Answer is Option (a)
Q.48: The value of x (length of rectangular field) is
(a) 150 m
(b) 400 m
(c) 200 m
(d) 320 m
Correct Answer is Option (c)
We have,
Q.49: The value of y (breadth of rectangular field) is
(a) 150 m
(b) 200 m
(c) 430 m
(d) 350 m
Correct Answer is Option (a)
Q.50: How much is the area of rectangular field?
(a) 60000 sq.m.
(b) 30000 sq.m.
(c) 30000 m
(d) 3000 m
Correct Answer is Option (b)
Area of rectangular field
= xy
= 200 × 150
= 30000 sq.m
|
204 videos|290 docs|139 tests
|