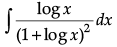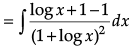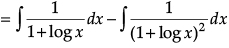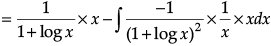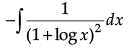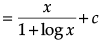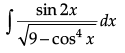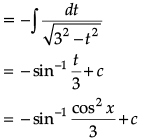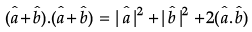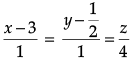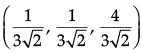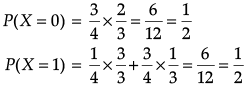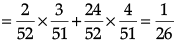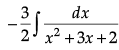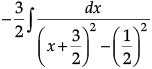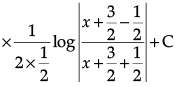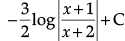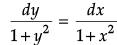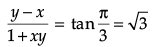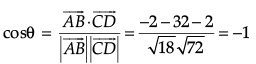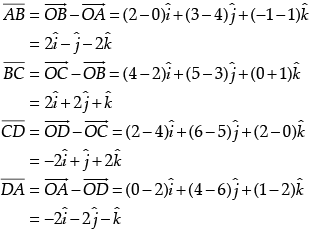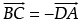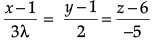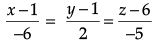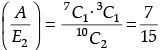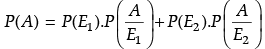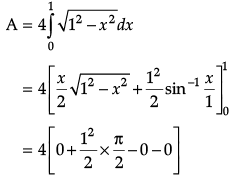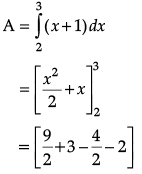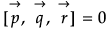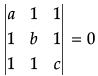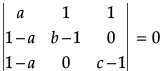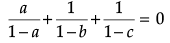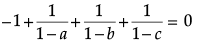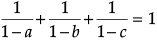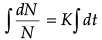Class 12 Mathematics: CBSE Sample Question Paper- Term II (2021-22)- 2 | Sample Papers for Class 12 Medical and Non-Medical PDF Download
| Table of contents |

|
| Class-XII |

|
| Time: 120 Minutes |

|
| Max. Marks: 40 |

|
| Section - A |

|
| Section - B |

|
| Section - C |

|
Class-XII
Time: 120 Minutes
Max. Marks: 40
General Instructions :
- This question paper contains three section A, B and C. Each part is compulsory.
- Section - A has 6 short answer type (SA1) questions of 2 marks each.
- Section - B has 4 short answer type (SA2) questions of 3 marks each.
- Section - C has 4 long answer type questions (LA) of 4 marks each.
- There is an internal choice in some of the questions.
- Q14 is a case-based problem having 2 sub parts of 2 marks each.
Section - A
Q.1. Find 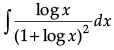
OR
Find : 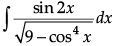
OR
Put cos2x = t
⇒ -2cos x sinx dx = dt
⇒ sin 2x dx = -dt
The given integral
Q.2. Write the sum of the order and the degree of the following differential equation:
(d/dx)(dy/dx) = 5
Order = 2
Degree = 1
Sum = 3
Q.3. If 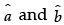 are unit vectors, then prove that
are unit vectors, then prove that  where θ is the angle between them.
where θ is the angle between them.
1 + 1 + 2cosθ
= 2(1 + cosθ) = 4cos2(θ/2)
∴= 2cos(θ/2)
Q.4. Find the direction cosines of the following line: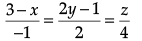
The given line is
Its direction ratios are <1, 1, 4>
Its direction cosines are
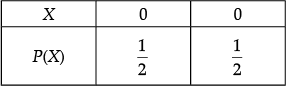
Q.5. A bag contains 1 red and 3 white balls. Find the probability distribution of the number of red balls if 2 balls are drawn at random from the bag one-by-one without replacement.
Let X be the random variable defined as the number of red balls.
Then X = 0, 1
Probability distribution Table:
Q.6. Two cards are drawn at random from a pack of 52 cards one-by-one without replacement. What is the probability of getting first card red and second card Jack?.
The required probability = P((The first is a red jack card and The second is a jack card) or (The first is a red non-jack card and The second is a jack card))
Section - B
Q.7. Find 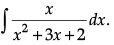
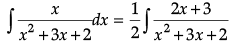
= 1/2(log)|x2 + 3x + 2|
= (1/2)log|x2 + 3x + 2| - (3/2)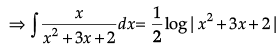
Q.8. Find the particular solution of the differential equation 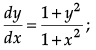 given that y(0) = √3.
given that y(0) = √3.
OR
Prove that x2 – y2 = C(x2 + y2)2 is the general solution of the differential equation (x3 – 3xy2) dx = (y3 – 3x2y) dy, where C is a parameter.
From the given, equation,
Integrating, we get tan-1 y = tan-1x + C
As x = 0, y =√3 so tan–1√3 = C or C= π/3
Now, the required solution
tan-1y = tan-1 x + (π/3)
y - x = √3 (1 + xy)
OR
x2 - y2 = C(x2 + y2)2 ...(i)
Differentiating above
2x - 2yy' = 2C (x2 + y2)(2x + 2yy')
or (x - yy') =using eq . (i)
or(y2 + x2)(x - yy') = (x2- y2)(2x +2yy') - (y2 + x2)yy1 + x(y2 + x2) = (x2 - y2)2x + (x2 - y2)2yy1
[2y(x2 - y2) + y(y2 - x2)] (dy/dx) = 2x(x2 - y2) - x(y2 - x2)
or (y3 - 3x2y)(dy/dx) = (x3 - 3xy2)
or (y3 - 3x2y)dy = (x3 - 3xy2)dx
Hence x2 – y2 = C(x2 + y2)2 is the solution of given differential equation.
Q.9. If 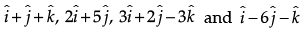 respectively are the position vectors of points A, B, C and D, then find the angle between the straight lines AB and CD. Find whether
respectively are the position vectors of points A, B, C and D, then find the angle between the straight lines AB and CD. Find whether 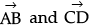 are collinear or not.
are collinear or not.
OR
Find the area of the quadrilateral ABCD, where A(0, 4, 1), B(2, 3, –1), C(4, 5, 0) and D(2, 6, 2).
Let required angle be θ.
Then
⇒ θ = 180° or π
Since θ = π soare collinear.
OR
We have, A(0, 4, 1), B(2, 3, –1), C(4, 5, 0) and D(2, 6, 2).
Since,and
Thus quadrilateral formed is parallelogram.
∴ Area of quadrilateral ABCD
= 9 sq. units.
Q.10. If the lines 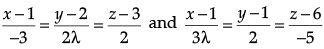 are perpendicular, find the value of λ. Hence find whether the lines are intersecting or not.
are perpendicular, find the value of λ. Hence find whether the lines are intersecting or not.
The equations of the given lines are:
and
On comparing these lines with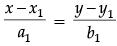
we get a1 = –3, b1 = 2λ, c1 = 2 and a2 = 3λ, b2 = 2, c2 = –5
Since, lines are perpendicular, a1a2 + b1b2 + c1c2 = 0
So, (–3) (3λ) + (2λ) (2) + (2) (–5) = 0
⇒ –9λ + 4λ – 10 = 0
⇒ –5λ – 10 = 0
⇒ –5λ = 10
⇒ λ = –2
Hence, for λ = –2 the given lines are perpendicular.
Now, given lines can be written as after substituting value of λ = –2and
The coordinate of any point on first line are given by(say)
or
x = -3r + 1, y = -4r + 2, z = 2r + 3
So, the coordinates of a general point on first line are (–3r + 1, –4r + 2, 2r + 3).
The coordinates of any point on second line are given by(say)
or x = -6s + 1, y = 2s + 1, z = -5s + 6
So, the coordinates of a general point on second line are (–6s + 1, 2s + 1, –5s + 6)
If the lines intersect, then they have a common point. So, for some value of λ and μ, we must have –3r + 1 = –6s + 1, –4r + 2 = 2s + 1, 2r + 3 = –5s + 6
or r = 2s, –4r – 2s = –1, 2r + 5s = 3
Solving first two of these two equations, we get r = 1/5 and s = 1/10. These values of r and s do not satisfy the third equation.
Hence, the given lines do not intersect.
Section - C
Q.11. A bag A contains 4 black and 6 red balls and bag B contains 7 black and 3 red balls. A die is thrown. If 1 or 2 appears on it, then bag A is chosen, otherwise bag B. If two balls are drawn at random (without replacement) from the selected bag, find the probability of one of them being red and another black.
Let E1 =Selecting bag A and E2 = Selecting bag B
∴ Probability for selecting bag when die is thrown P(E1) = 1/3 and probability for selecting bag when die is thrown P(E2) = 2/3Let A = Getting one red and one black ball
∴and
= 22/45
Q.12. Find the area of the region bounded by the circle x2 + y2 = 1.
OR
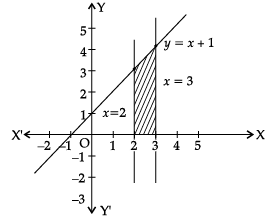
Find the area of the region bounded the curve y = x + 1 and the lines x = 2 and x = 3.
We have, x2 + y2 = 1, which is a circle having centre at (0, 0) and radius ‘1’ unit.
⇒ y2 = 1 - x2
From the figure, area of the shaded region,
= π sq. units
OR
Given : Curve y = x + 1 and lines x = 2, x = 3
If x = 2 ⇒ y = 3
If x = 3 ⇒ y = 4
So, intersection points (2, 3) and (3, 4)From the figure, area of the shaded region,
= (7/2) sq. units
Q.13. If the vector 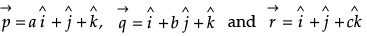 are coplanar, then for a, b, c ≠ 1, then show that.
are coplanar, then for a, b, c ≠ 1, then show that. 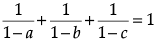
Since the vector
are coplanar,
∴
i.e.,
R2 → R2 → R1 and R3 → R3 → R1,
or
or a(b - 1)(c - 1)-1(1 - a)(c - 1)-1(1 - a)(b - 1) = 0
i.e., a (1 - b)(1 - c) + (1 - a)(1 - c) + (1 - a)(1 - b) = 0
Dividing both the sides by (1 – a)(1 – b)(1 – c), we get
i.e.,
i.e.,
Case-Based/Data Based
Q.14. The rate of increase in the number of bacteria in a certain bacteria culture is proportional to the number present. Given that the number triples in 5 hours.
Based on the above information, answer the following questions:
(i) If ‘N’ is the number of bacteria, then find the differential equation. Also, find the general solution of obtained differential equation.
(ii) If N0 is the initial count of bacteria, the find the bacteria count after 10 hours.
(i) Given that N is the number of bacteria.
dN/dt ∝ N
⇒ dN/dt ∝ KN is the required differential equation.
Now, dN/N ∝ K dt
⇒ log|N| = Kt + c,
which is the general solution of differential equation. ...(1)
(ii) Given, when t = 0, N = N0, from (1)
log|N0| = c
∴ (1) ⇒ log|N| = Kt + log|N0|
⇒ log|N/N0| = Kt ...(2)
Given, when t = 5, N = 3N0
From (2), log|3| = 5K
⇒ K = (1/5) log3
∴ Particular solution is...(3)
when t = 10
log|N/N0| =2 log 3 = log 9
⇒ N/N0 = 9
⇒ N = 9N0.
|
159 docs|4 tests
|