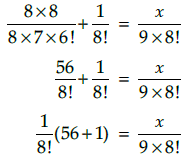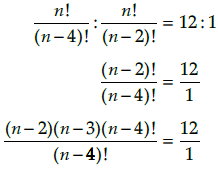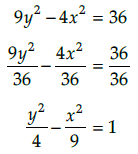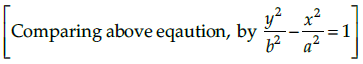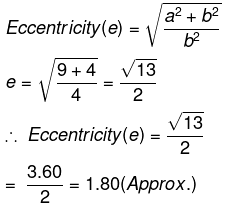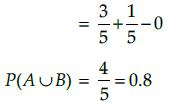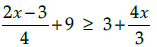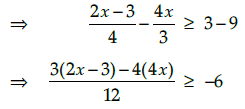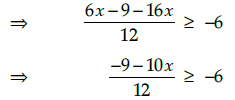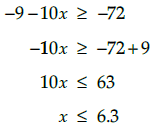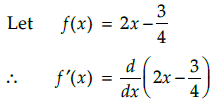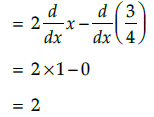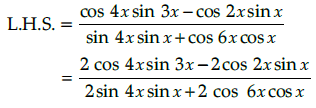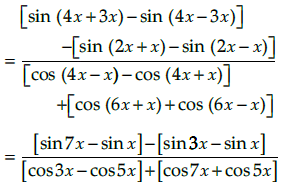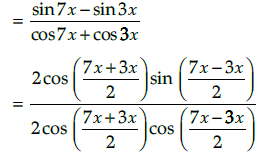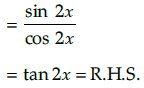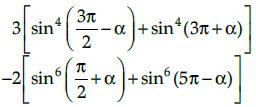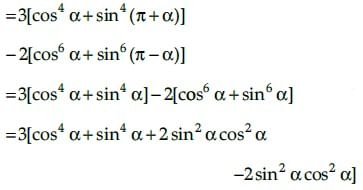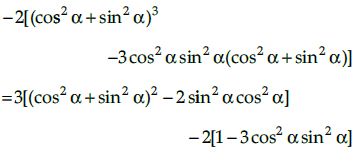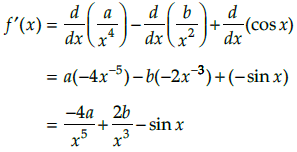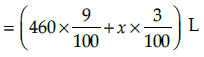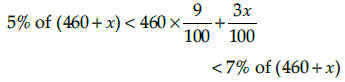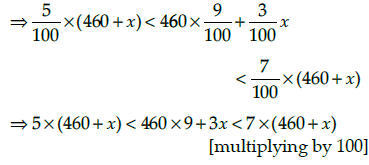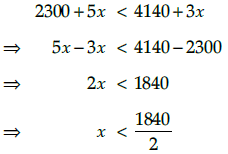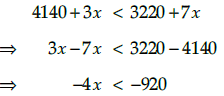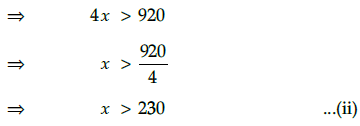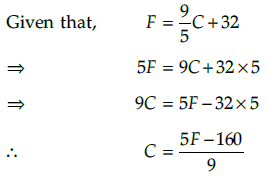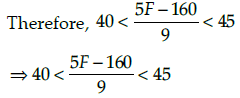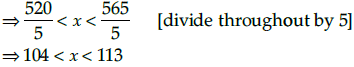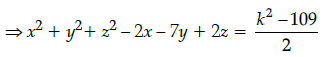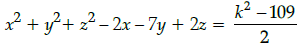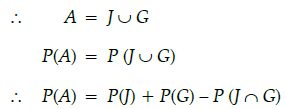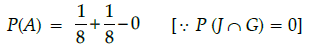Class 11 Math: CBSE Sample Question Papers- Term II (2021-22)- 2 | Sample Papers for Class 11 Medical and Non-Medical - JEE PDF Download
Class XI: Mathematics
Time: 120 Minutes
Max. Marks: 40
General Instructions:
- This question paper contains three sections A, B and C. Each part is compulsory.
- Section - A has 6 short answer type (SA1) questions of 2 marks each.
- Section - B has 4 short answer type (SA2) questions of 3 marks each.
- Section - C has 4 long answer type questions (LA) of 4 marks each.
- There is an internal choice in some of the questions.
- Q14 is a case-based problem having 2 sub parts of 2 marks each.
Section - A
Q.1. 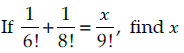
OR
If nP4 : nP2 = 12 : 1, find n
nP4 : nP2 = 12 : 1
(n-2)(n-3) = 12
n2-5n-6 =0
(n-6)(n+1) =0if n+1 =0
∴ n=-1 is not possible (n ∈ N)
if n-6=0
∴ n=6
Q.2. Write the eccentricity of the hyperbola, 9y2 – 4x2 = 3
a2 = 9, b2 = 4
Q.3. How many 5 digit telephone numbers can be constructed using the digits 0 to 9, if each number starts with 67 and no digit appears more than once?
Number of ways to fill the III place = 8
Number of ways to fill the IV place = 7
Number of ways to fill the V place = 6
Hence, total number of ways
= 8 x 7 x 6 = 56 x 6 = 336
OR
Determine the number of 5 card combining out of deck of 52 cards if each selection of 5 cards has exactly one king.
1 king out of 4 kings can be selected in 4C1 ways
Remaining 4 cards out of remaining 48 cards can be selected in 48C4 ways.
Hence, total number of ways
= 4C1 x 48C4=4 x 48C4
Q.4. Given P(A) = 3/5 and P(B)= 1/5. Find P(A ∪ B) if A and B are mutually exclusive events.
P(A) = 3/5 and P(B)= 1/5
A and B are mutually exclusive events
∴ P(A∩B) =0
Now P(A∪B)= P(A) + P(B) - P(A∩B)
Q.5. Solve for 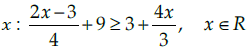
We have,
Q.6. Find the derivatives of 2x - 3/4
Section - B
Q.7. If tan θ + sin θ = m and tan θ – sin θ = n, then prove that : m2 – n2 = 4sinθ⋅tan θ
Given, tan θ + sin θ = m and tan θ - sin θ = n,
To prove, m2 – n2 = 4 sin θ tan θ
L.H.S. = m2-n2
= (m+n)(m-n)
= [(tan θ + sin θ) + (tan θ - sin θ) ]. [(tan θ + sin θ) - (tan θ - sin θ)]= (2 tan θ) (2sin θ)
= 4sin θ tan θ
= R.H.S
Hence Proved
Q.8. Prove that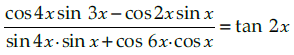
OR
Prove that:
tanα.tan (60º - α). tan (60º + α)= tan 3α
Hence Proved
Q.9. If tan (A + B) = p, tan (A – B) = q, then show that : 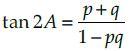
Given, tan (A + B) = p, and tan (A – B) = q,
L.H.S. = tan 2A = tan(A+B+A-B)
= tan[(A+B)+(A-B)]
Q.10. Find the value of the expression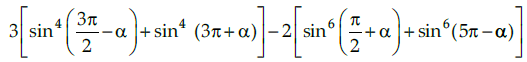
Given,
Section - C
Q.11. Find the derivative of the functions 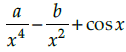 where a and b are non-zero constant.
where a and b are non-zero constant.
Let
Q.12. A solution of 9% acid is to be diluted by adding 3% acid solution to it. The resulting mixture is to be more than 5% but less than 7% acid. If there is 460 L of the 9% solution, how many litres of 3% solution will have to be added?
Let x L of 3% solution be added to 460 L of 9% solution of acid.
Then, total quantity of mixture = (460 + x) L
Total acid content in the (460 + x) L of mixture
It is given that acid content in the resulting mixture must be more than 5% but less than7%.
Therefore,⇒ 2300 + 5x < 4140 + 3x < 3220 + 7x
Taking first two inequalities,
⇒ x<920 ...(i)
Taking last two inequalities,Hence, the number of litres of the 3% solution of acid must be more than 230 L and less than
920 L.
OR
A solution is to be kept between 40°C and 45°C. What is the range of temperature in degree Fahrenheit, if the conversion formula is F = 9/5C+32?
Let the required temperature be x° F.
Since, temperature in degree Celsius lies between 40°C to 45°C.
⇒ 40 x 9 < 5x - 160 < 45 x 9 [multiplying throughout by 9]
⇒ 360 < 5x - 160 <405 [adding 160 throughout]
⇒ 360 + 160 < 5 < 405 + 160
⇒ 520 < 5x < 565Hence, the range of temperature in degree Fahrenheit is between 104 °F to 113°F.
Q.13. If A and B be the points (3, 4, 5) and (–1, 3, –7), respectively, find the equation of the set of points P such that PA2 + PB2 = k2, where k is constant.
The coordinates of points A and B are given as (3, 4, 5) and (–1, 3, –7) respectively. Let the
co-ordinates of point P be (x, y, z).
On using distance formula, we obtain
PA2 = (x – 3)2 + (y – 4)2 + (z – 5)2
= x2 + 9 – 6x + y2 + 16 – 8y + z2 + 25 – 10z
= x2 + y2 + z2 – 6x – 8y – 10z + 50
PB2 = (x + 1)2 + (y – 3)2 + (z + 7)2
= x2 + 1 + 2x + y2 + 9 – 6y + z2 + 49 + 14z
= x2 + y2 + z2 + 2x – 6y + 14z + 59
Now, if PA2 + PB2 = k2, then
(x2 + y2 + z2 – 6x – 8y – 10z + 50) + (x2 + y2 +
z2 + 2x – 6y + 14z + 59)
⇒ 2x2 + 2y2 + 2z2 – 4x – 14y + 4z + 109 = k2
⇒ 2(x2 + y2 + z2 – 2x – 7y + 2z) + 109 = k2
⇒ 2(x2 + y2 + z2 – 2x – 7y + 2z) = k2 – 109
Thus, the required equation is
Case-Based/Data Based
Q.14. One of the four persons John, Rita, Aslam or Gurpreet will be promoted next month. Consequently the sample space consists of four elementary outcomes S = {John promoted, Rita promoted, Aslam promoted, Gurpreet promoted}. You are told that the chances of John's promotion is same as that of Gurpreet, Rita's chances of promotion are twice as likely as Johns. Aslam's chances are four times that of John.

Based on the given information, answer the following questions:
(i) What is the probability that John got promoted?
(ii) If A = {John promoted or Gurpreet promoted}, Find P(A).
Let Event :
J = John promoted
R = Rita promoted
A = Aslam promoted
G = Gurpreet promoted
Given sample space, S = {John promoted,
Rita promoted, Aslam promoted, Gurpreet promoted}
i.e., S = {J, R, A, G)
It is given that, chances of John’s promotion is same as that of Gurpreet.
P(J) = P(G)
Rita’s chances of promotion are twice as likely as John.
P(R) = 2P(J)
and Aslam’s chances of promotion are four times that of John.P(A) = 4P(J)
(i) P(J) + P(R) + P(A) + P(G) = 1
⇒ P(J) + 2P(J) + 4P(J) + P(J) = 1
⇒ 8P(J) = 1
P(J) = P(John Promoted) = 1/8
(ii) A = John promoted or Gurpreet promoted
= 1/4