Word Problem: Fractions | Mathematics for Class 4 PDF Download

Q1: Johnny ate 3/4 of a pizza, and Emily ate 6/8 of a pizza. Are they talking about the same amount of pizza?
Sol: To check if they ate the same amount of pizza, we need to check if the fractions are equivalent.
In this case, we can see that 3/4 is equivalent to 6/8 because if we multiply 3/4 by 2/2, we get 6/8.
So, Yes they are talking about the same amount of pizza.

Q2: Sarah cut a cake into 8 equal pieces and ate 3/8 of it. Jack cut a cake into 10 equal pieces and ate 5/10 of it. Did they eat the same amount of cake? 
Sol: Sarah ate 3 out of 8 pieces of cake (3/8).
Jack ate 5 out of 10 pieces of cake (5/10).
To check if they ate the same amount, we simplify the fractions.
3/8 is not equivalent to 5/10 because when simplified, they become 3/8 and 1/2, which is not equal.
Therefore, they did not eat the same amount of cake.

Q3: Mary bought 4/3 kg  of beef. She cooked  3/4 kg of it for lunch. How much beef did she cook ?
Sol: Quantity of beef that she bought  =  4/3 kg
Quantity of beef that she cooked  =  3/4 kg
Remaining quantity of beef after used  =  (4/3) x (3/4)
=  (4 ⋅ 3)/12
=  1 kg

Q4: Jennifer had 18 picture cards. She gave 1/3 of them to Mary. How many picture cards does she have now?
Sol: No. of picture cards does Jennifer have  = 18
No. of picture cards gave to Mary = 18 ⋅ (1/3)          
=  18/3
=  6
Remaining number of pictures Jennifer have now
=  Original number of pictures - Number of pictures gave to Mary
=  18 - 6
=  12

Q5: Mr. John weighs 80 kg. His son is 3/5 as heavy. Find their total weight.
Sol: Weight of John  =  80 kg
Weight of his son  =  80 ⋅ (3/5)
=  (80 ⋅ 3)/5
=  240/5
=  48 kg
Total weight  =  Weight of John + Weight of his son
=  80 kg + 48 kg
=  128 kg

Q6: Sam is standing on the number line at the point 2/3. His friend, Lily, is standing at the point 1/4. Who is closer to 0 on the number line?
Sol: Sam is standing at the point 2/3 on the number line, while Lily is standing at the point 1/4.
To compare who is closer to 0, let's find a common denominator.
To make the denominators the same, we need to find the least common multiple (LCM) of 3 and 4, which is 12.
Now, we can rewrite the fractions with the same denominator:
Sam: 2/3 = 8/12
Lily: 1/4 = 3/12
Comparing the fractions with the same denominator, we can see that 3/12 is smaller than 8/12. This means that Lily is closer to 0 on the number line than Sam.
Therefore, the correct answer is Lily.

Q7: Find the sum of the below fractions.
(7/11) + (2/11) = ____
Sol: The two fractions have like denominators so you can add the numerators. 
Then: 

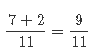This fraction cannot be reduced.

Q8: Maddy reads three-fifth of the 75 pages of his lesson. How many more pages does he need to complete the lesson?
Sol: Maddy reads = 3/5 of 75
= 3/5 × 75
= 45 pages
Maddy has to read = 75 – 45.
= 30 pages.
Therefore, Maddy has to read 30 more pages.

Q9: Tina has a pizza that is divided into 8 equal slices. She eats 3/8 of the pizza. How much pizza is left?
Sol: Subtract the fraction that Tina ate from the whole pizza.
Whole pizza = 8/8 (since it is divided into 8 equal slices)
Pizza eaten by Tina = 3/8
To find the remaining pizza, we subtract 3/8 from 8/8
= 8/8 - 3/8 = 5/8
Therefore, 5/8 of the pizza is left after Tina ate 3/8 of it.

Q10: A frog took three jumps. The first jump was 2/3 m long, the second was 5/6 m long and the third was 1/3 m long. How far did the frog jump in all?
Sol: To find the total distance the frog jumped, we need to add up the lengths of its three jumps.
= The length of the first jump: 2/3 m
= The length of the second jump: 5/6 m
= The length of the third jump: 1/3 m
To add fractions with different denominators, we need to find a common denominator. The least common multiple (LCM) of 3 and 6 is 6.
Now, let's convert the fractions to have a denominator of 6:
= The length of the first jump: (2/3) x (2/2) = 4/6 m
= The length of the second jump: (5/6) x (1/1) = 5/6 m
= The length of the third jump: (1/3) x (2/2) = 2/6 m
Now, we can add the fractions:
= 4/6 + 5/6 + 2/6 = 11/6
The frog jumped a total distance of 11/6 m.