Knowing Our Numbers Class 6 Notes Maths Chapter 1
Introduction
Numbers help us count and measure things. We can use them to do cool stuff like adding, taking away, multiplying, and sharing. Today, we're going to learn how to look at numbers and see which ones are bigger or smaller, and find out which number is the biggest and which one is the smallest.

Numbers are values we use in math. They tell us how big or small things are.
Comparing numbers

- When we compare numbers, we're figuring out if one number is bigger, smaller, or the same as the other.
- If two numbers have unequal numbers of digits, then the number with the greater number of digits is greater.
- If two numbers have an equal number of digits, then the number with a greater valued digit on the extreme left is greater. If the digits on the extreme left of the numbers are equal, then the digits to the right of the extreme left digits are compared, and so on.

- For example, take 24 and 36.
We see that 36 is larger because it has more tens and ones. - Even when dealing with bigger numbers like 5005 and 5010, we look at each part of the number to compare.
In this case, 5010 is larger because it has more tens and ones. - Shifting digits means moving numbers to different places to compare them fairly.
- Let's say we have 787. If we switch the 8 and 7, making it 778, we can tell that 787 is still bigger because it has a higher value in the tens place.
- However, if all the digits are the same, like in 777, shuffling them around won't change the number.
Proper Order
- If we arrange the numbers from the smallest to the greatest, then it is said to be an Ascending order. An ascending order is also sometimes called an increasing order.
- If we arrange the numbers from the greatest to the smallest, then it is said to be Descending order.

How many numbers can be formed using a certain number of digits?
- When we're given a set of digits like 3, 0, 9, and 6, we have the flexibility to create different numbers by rearranging these digits.
- Let's explore this with the aim of finding both the largest and smallest possible numbers using these four digits.
- Starting with the largest number, we arrange the digits in descending order: 9, 6, 3, and 0.
This gives us the number 9630. - Conversely, to find the smallest number, we need to be mindful of the fact that a four-digit number can't begin with 0.
So, we arrange the digits in ascending order, ensuring that 0 is not the leftmost digit: 3, 0, 6, and 9. This gives us the number 3069.
Thus, with the same set of digits, we can generate two distinct numbers—
(i) one representing the largest possible value and,
(ii) other the smallest—simply by rearranging their positions.
Shifting Digits
- Changing the position of digits in a number changes the magnitude of the number.
- Example: Consider the number 789.
If we swap the hundredth place digit with the digit at the unit place, we will get 987, which is greater than 789. - Similarly, if we exchange the tenth place with the unit place, we get 798, which is greater than 789.
 Example of Shifting Digits
Example of Shifting Digits
Place Value of Digit
- Place value describes the position or place of a digit in a number.
- Each digit has a place in a number. When we represent the number in general form, the position of each digit will be expanded.
- Those positions start from a unit place, or what we also call one’s position.
- The order of place value of digits of a number from right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.

Example
5,46,851 = 5 × 1,00,000 + 4 × 10,000 + 6 × 1,000 + 8 × 100 + 5 × 10 +1 × 1
- This number has 1 at one’s place, 5 at tens place, 8 at hundreds place, 6 at thousands place, 4 at ten thousands place and 1 at lakh place.
- Number Names are also written based on the place value name. So its number is five lakh forty-six thousand eight hundred fifty-one.
We can use the table format below to easily read and write the number.

Estimation of the Numbers
- When there is a very large figure, we approximate that number to the nearest plausible value. This is called estimation.
- A quick, rough estimate of the result of number operations can be done by rounding off the numbers is involved.

Rules of Estimation
- To round off numbers to the nearest tens, round off numbers 1, 2, 3, and 4 to 0 and numbers 6, 7, 8, and 9 to 10.
- To estimate numbers to the nearest hundred, round numbers 1 to 49 to 0 and numbers 51 to 99 to 100.
- To estimate numbers to the nearest thousands, round off the numbers 1 to 499 to 0 and 501 to 999 to 1000.
Estimation involves approximating a quantity to the accuracy required. We can apply the above rules depending on the accuracy required.
We can estimate sum, difference, and multiplication by applying the estimation rules. We can apply the above rules depending on the accuracy required and how quickly the answer can be found.
Estimating sum or difference
- Estimations are used to add and subtract numbers.
- An additional example of estimation is Estimate 7890 + 437.
Here 7890 > 437.
Therefore, round off to hundreds.
7890 is rounded off to 7900
437 is rounded off to + 400
Estimated Sum = 8300
Actual Sum = 8327
- Example of estimation in subtraction: Estimate 5678 – 1090.
Here 5678 > 1090.
Therefore, round off to thousands.
5678 is rounded off to 6000
1090 is rounded off to – 1000
Estimated Difference = 5000
Actual Difference = 4588

Estimating products of numbers
- Round off each factor to its greatest place, then multiply the rounded off factors.

- Example of estimation in Multiplication: Estimating the product of 199 and 31:
199 is rounded off to 200
31 is rounded off to 30
Estimated Product = 200 × 30 = 6000
Actual Result = 199 × 31 = 6169
Use of Commas
- Commas added to numbers help us read and write large numbers easily.
- As per Indian Numeration, Commas are used to mark thousands, lakhs and crores.
- The first comma comes after hundreds place (three digits from the right) and marks thousands.
- The second comma comes two digits later (five digits from the right). It comes after ten thousand place and marks lakh.
- The third comma comes after another two digits (seven digits from the right). It comes after ten lakh place and marks crore
- Examples
1, 08, 01, 992
2, 32, 40, 581
3, 17, 05, 062
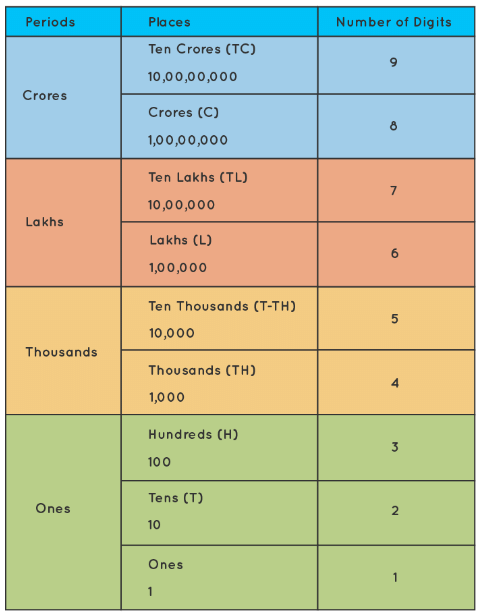 Indian Numeral System
Indian Numeral System
Note: We do not use commas while writing number names
International System of Numeration
Values of the places in the International system of numeration are Ones, Tens, Hundreds, Thousands, Ten thousands, Hundred thousands, Millions, Ten millions and so on.
1 million = 1000 thousands,
1 billion = 1000 millions
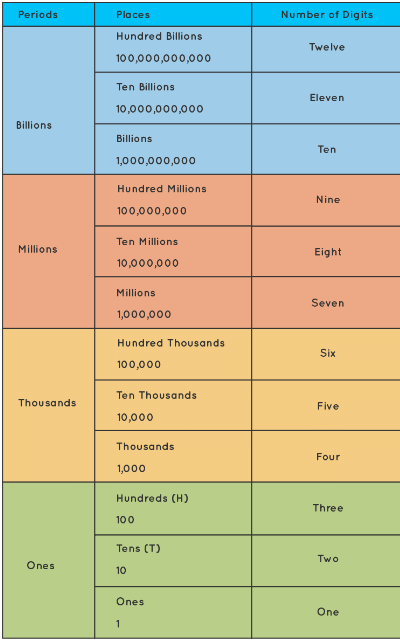 International System of Numeration Example: 341,697,832
International System of Numeration Example: 341,697,832
Expanded form:
3 x 100,000,000 + 4 x 10,000,000 + 1 x 1,000,000 + 6 x 100,000 + 9 x 10,000 + 7 x 1,000 + 8 x 100 + 3 x 10 + 2 x 1
Note: If we have to express the numbers larger than a million then we use a billion in the International System of Numeration:
1 billion = 1000 million
|
30 videos|120 docs|59 tests
|
FAQs on Knowing Our Numbers Class 6 Notes Maths Chapter 1
| 1. How can we compare numbers using place value of digits? |  |
| 2. How can we determine the proper order of numbers with different digits? |  |
| 3. How many numbers can be formed using a certain number of digits? |  |
| 4. How can we shift digits in a number to form a new number? |  |
| 5. How can we estimate numbers using the place value of digits? |  |

















