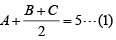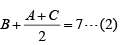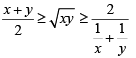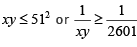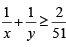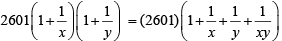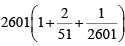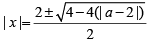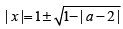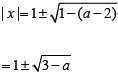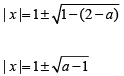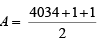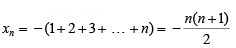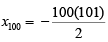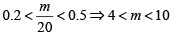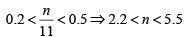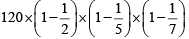CAT 2020: Numbers | Additional Study Material for CAT PDF Download
Q.1. If a, b and c are positive integers such that ab = 432, bc = 96 and c < 9, then the smallest possible value of a + b + c is [2020]
(a) 56
(b) 59
(c) 49
(d) 46
Correct Option is D
Given ab = 432, bc = 96 and c < 9
To find the minimum value for a + b + c, the two larger numbers should be as close as possible.
The closest combination whose product is 432 is 18 x 24 . For b = 24, we get c = 4 and a = 18 .
Hence the least value for a + b + c = 46 .
Q.2. How many 3-digit numbers are there, for which the product of their digits is more than 2 but less than 7? [2020]
Ans: 21
The product of the digits of the three-digit numbers should be more than 2 and less than 7 .
Hence the possible numbers are as follows.
Q.3. The mean of all 4 -digit even natural numbers of the form 'aabb', where a >0, is [2020]
(a) 5050
(b) 4466
(c) 5544
(d) 4864
Correct Option is C
The sum of possible even digit numbers in the form aabb is 1100 + 1122 + 1144 + 1166 + 1188 + 2200 + 2222 + 2288 + ......9900 + 9922 + 9988 i.e. (45 numbers)
⇒ 1100 + 1100 +1100+ 1100 + 1100 + 22 + 44 + 66 + 88 + 2200 + 2200 + 2200 + 2200 + 2200 +22 + 44 + 66 + 88 +… + 9900 + 9900 + 9900 + 990 + 9900 + 22 + 44 + 66 + 88
⇒ 5(1100 + 2200 + .....9900) + 9(22 + 44 + 66 + 88)5 x 1100(1 + 2 + .... 9) + 9 x 22(1 + 2 + 3 + 4)
⇒ 5500(45) + 45 ´ 44 = 45(5544)
Hence mean =5544
Q.4. Let A, B and C be three positive integers such that the sum of A and the mean of B and C is 5. In addition, the sum of B and the mean of A and C is 7. Then the sum of A and B is [2020]
(a) 6
(b) 5
(c) 7
(d) 4
Correct Option is A
Given A, B and C are positive integers such that
The least value for A=1 in which case B=5.
Hence A + B = 6
Q.5. If x and y are positive real numbers satisfying x + y=102, then the minimum possible value of 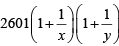 is [2020]
is [2020]
Ans: 2704
AM ≥ GM ≥ HM
Given x + y = 102
⇒
⇒
The minimum value of
=
= 2704
Q.6. How many 4-digit numbers, each greater than 1000 and each having all four digits distinct, are there with 7 coming before 3? [2020]
Ans: 315
Consider four blanks
7 is in thousand place, then 3 can be placed in any of the 3 places in 3 ways. Remaining two blanks can be filled with remaining eight digits in 8P2 ways. The number of numbers that have 7 is in thousand place is 3 x 8P2 = 168
Thousand place cannot be 0,7 and 3, it can be filled with remaining 7 digits in 7 ways. In remaining 3 blanks, 7 and 3 can be arranged in 3 ways. Fourth blank can be filled in 7 ways. The number of numbers that are formed where 7 and 3 is not in thousand place is 7 x 3 x 7 = 147 . Hence total required numbers = 168 + 147 = 315 .
Q.7. In how many ways can a pair of integers (x , a) be chosen such that x2 - 2| x| + | a - 2| = 0? [2020]
(a) 4
(b) 5
(c) 6
(d) 7
Correct Option is D
x2 - 2| x| + | a- 2 |= 0
If a > 2; | a - 2 |= a - 2
since x is integer 3 - a ≥ 0
a ≤ 3
The possible values of a is = 3
Then x = ± 1;
If a = 2, | x |=| 1 ± 1 |, ⇒ x = ± 2, 0
If a < 2, | a - 2 |= 2 - a
Since x is integer a -1 ≥ 0 ⇒ a ≥ 1
∴ The possible values of a is 1
If a = 1, | x |= 1 ⇒ x = ± 1
∴ The possible pairs =(-1,3), (1,3), (1,1), (-1,1), (2,2),(-2,2), (0,2) i.e., 7
Q.8. The number of integers that satisfy the equality ( x2 - 5x + 7 ) x+1 = 1 is [2020]
(a) 2
(b) 3
(c) 5
(d) 4
Correct Option is B
( x2 - 5x + 7 ) x+1 = 1
We know, for ab = 1,
if -a = -1 then b is even.
-a = 1 then b is any number
-a > 0 then b = 0
Case 1: x + 1 = 0 Þ x = -1
Case 2: x2 -5x+7 =1 ⇒ x2 -5x + 6 = 0 ⇒ x = 2 or 3
Case 3: x2 -5x + 7 = -1 ⇒ x2 -5x + 8 = 0
but x is not an integer
∴ The number of integers satisfies the equation is 3
Q.9. The number of pairs of integers (x , y) satisfying x ≥ y ≥ -20 and 2 x + 5 y = 99 is [2020]
Ans: 17
2 x + 5 y = 99
When y = - 19, x = 97; since x ≥ y ; the maximum value of y is 13 and corresponding value of x is 17.
We know that the solutions of y are in arithmetic progression with common difference 2.
Here a = - 19, d = 2, tn = 13
tn = a + (n -1)d
-19 + (n - 1)(2) = 13
(n - 1)2 = 32 ⇒ n = 17
Hence number of pairs integers is 17
Q.10. If x and y are non-negative integers such that x + 9 = z, y + 1 = z and x + y < z + 5, then the maximum possible value of 2x + y equals [2020]
Ans: 23
Given x + 9 = z = y + 1 and x + y < z + 5
⇒ (z -9) + (z - 1) < z + 5
⇒ z < 15
Hence the maximum value of z = 14, max of x = 5 and max of y = 13
Required answer, 2 x + y = 2 x 5 + 13 = 23
Q.11. How many pairs (a, b) of positive integers are there such that a ≤ b and ab = 42017 ? [2020]
(a) 2017
(b) 2019
(c) 2020
(d) 2018
Correct Option is B
Given, a × b = 42017 = 24034
Since a × b = 42017 , is a perfect square the number of factors of 24034 is odd.
Required answer, the number of values of
= 2018
Q.12. If x1 = -1 and xm = xm +1 + (m + 1) for every positive integer $m,$ then x100 equals [2020]
(a) -5151
(b) -5150
(c) -5051
(d) -5050
Correct Option is D
xm + 1 = xm - (m + 1)
x2 = x1 - 2 = -1 - 2 = -3
x3 = x2 - 3 = -1 - 2 - 3 = - 6
Similarly,
Hence,
= -5050
Q.13. Let m and n be natural numbers such that n is even and 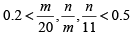 . Then m - 2n equals [2020]
. Then m - 2n equals [2020]
(a) 3
(b) 4
(c) 1
(d) 2
Correct Option is C
Given,
⇒ n = 4
since 0.2 < n/m < 0.5 m and n = 4, m = 9
m - 2n = 9 - 2 x 4 = 1
Q.14. Let N, x and y be positive integers such that N = x + y, 2 < x < 10 and 14 < y < 23. If N > 25, then how many distinct values are possible for N? [2020]
Ans: 6
Given, 2 < x < 10 and 14 < y < 23 Þ 17 < ( x + y ) < 32 i.e. 17 < N < 32
But N > 25 hence 25 < N < 32
N can take 6 distinct values.
Q.15. How many of the integers 1, 2, … , 120, are divisible by none of 2, 5 and 7? [2020]
(a) 40
(b) 42
(c) 43
(d) 41
Correct Option is D
The required answer
=
= 41.14
Required answer is the integral part of 41.14 = 41
|
5 videos|385 docs|204 tests
|
FAQs on CAT 2020: Numbers - Additional Study Material for CAT
| 1. What is CAT 2020 and when will it be conducted? |  |
| 2. How can I apply for CAT 2020? |  |
| 3. What is the eligibility criteria for CAT 2020? |  |
| 4. How is CAT 2020 different from previous years' exams? |  |
| 5. How can I prepare for CAT 2020 effectively? |  |