Venn Diagrams & Set Theory CAT Previous Year Questions with Answer PDF
2024
Passage
Answer the following questions based on the information given below.
The chart below provides complete information about the number of countries visited by Dheeraj, Samantha and Nitesh, in Asia, Europe and the rest of the world (ROW).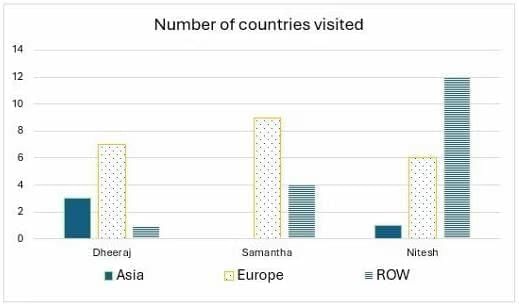 The following additional facts are known about the countries visited by them.
The following additional facts are known about the countries visited by them.
1. 32 countries were visited by at least one of them.
2. USA (in ROW) is the only country that was visited by all three of them.
3. China (in Asia) is the only country that was visited by both Dheeraj and Nitesh, but not by Samantha.
4. France (in Europe) is the only country outside Asia, which was visited by both Dheeraj and Samantha, but not by Nitesh.
5. Half of the countries visited by both Samantha and Nitesh are in Europe.
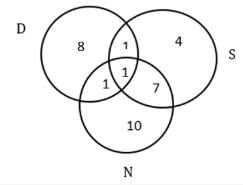
Q1: How many countries in Asia were visited by at least one of Dheeraj, Samantha and Nitesh?
Ans: 3
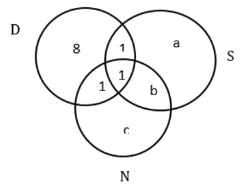
Sol: First, tabulate the given information,
It is given that the USA is the only country that was visited by all three of them.
And with statements 3 and 4 we get the following Venn diagram.
Now from statement 1, we can say that a+b+c = 32 – 11 = 21
We know that a +b = 13 – 2 = 11
So, c = 21 – 11 = 10
Similarly, we get a = 4 and b = 7
Number of Asian countries visited by Dheeraj = 3
Number of Asian countries visited by Nitesh = 1
Number of Asian countries visited by Samantha = 0
They both visited China. So, between them, a total of 4 countries were visited.
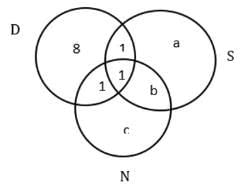
Q2: How many countries in Europe were visited only by Nitesh?
Ans: 2
Sol: First, tabulate the given information,
It is given that the USA is the only country that was visited by all three of them.
And with statements 3 and 4 we get the following Venn diagram.
Now from statement 1, we can say that a+b+c = 32 – 11 = 21
We know that a +b = 13 – 2 = 11
So, c = 21 – 11 = 10
Similarly, we get a = 4 and b = 7
From the last statement, we can say that both Nitesh and Samantha together visited 7+1/2 = 4 countries in Europe. No other person visited the same European country as Nitesh except for these 4 countries. Nitesh visited 6 – 4 = 2 countries in Europe alone.
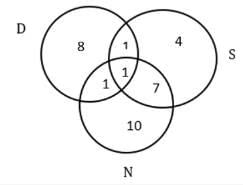
Q2: How many countries in the ROW were visited by both Nitesh and Samantha?
Ans: 4
Sol: First, tabulate the given information,
It is given that the USA is the only country that was visited by all three of them.
And with statements 3 and 4 we get the following Venn diagram.
Now from statement 1, we can say that a+b+c = 32 – 11 = 21
We know that a +b = 13 – 2 = 11
So, c = 21 – 11 = 10
Similarly, we get a = 4 and b = 7
Both Nitesh and Samantha visited 7+1/2 = 4 countries in ROW
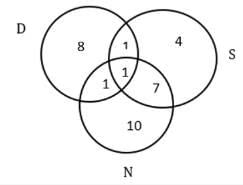
Q3: How many countries in Europe were visited by exactly one of Dheeraj, Samantha and Nitesh?
A:12
B: 14
C: 5
D: 10
Ans: a
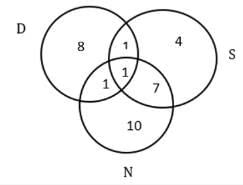
Sol: First, tabulate the given information,
It is given that the USA is the only country that was visited by all three of them.
And with statements 3 and 4 we get the following Venn diagram.
Now from statement 1, we can say that a+b+c = 32 – 11 = 21
We know that a +b = 13 – 2 = 11
So, c = 21 – 11 = 10
Similarly, we get a = 4 and b = 7
In Europe the number of countries visited by exactly one of Dheeraj, Samantha, and Nitesh = 6+4+2 = 12.
2022
Passage - 1
A speciality supermarket sells 320 products. Each of these products was either a cosmetic product or a nutrition product. Each of these products was also either a foreign product or a domestic product. Each of these products had at least one of the two approvals – FDA or EU.
The following facts are also known:
- Half of the domestic products were FDA approved cosmetic products.
- None of the foreign products had both the approvals, while 60 domestic products had both the approvals.
- There were 140 nutrition products, half of them were foreign products.
- There were 200 FDA approved products. 70 of them were foreign products and 120 of them were cosmetic products.
- There were equal numbers of domestic and foreign products.
Q1: How many foreign products were FDA approved cosmetic products?
Ans: 40
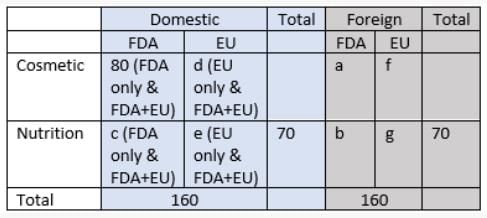
Sol:
According to the data given, we can create the following table:
a + b + c + 80 = 200
a + b = 70
=> c = 50
=> e = 20, d = 10
Also, 80 + a = 120
=> a = 40, b = 30, g = 40, f = 50
Now, we’ll also introduce x and y which are the Domestic nutrition products having both approvals and Domestic cosmetic products having both approvals. (x+y = 60)
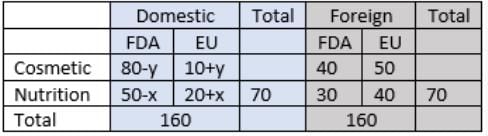
The final table is:40 foreign products were FDA approved cosmetic products.
Q2: How many cosmetic products did not have FDA approval?
(a) 10
(b) 60
(c) 50
(d) Cannot be determined
Ans: b
Sol:
10 domestic cosmetic and 50 foreign cosmetic products had only EU approvals, i.e., these 60 products did not have FDA approval.
Q3: Which among the following options best represents the number of domestic cosmetic products that had both the approvals?
(a) At least 10 and at most 80
(b) At least 20 and at most 70
(c) At least 20 and at most 50
(d) At least 10 and at most 60
Ans: d
Sol:
50-x ≥ 0
=> x max = 50
In that case, y = 10
x min = 0
=> y = 60
So, at least 10 and at most 60.
Q4: If 70 cosmetic products did not have EU approval, then how many nutrition products had both the approvals?
(a) 10
(b) 20
(c) 30
(d) 50
Ans: a
Sol:
80-y+40 = 70
=> y = 50
Since x+y = 60,
=> x = 10 nutrition products had both the approvals
Q5: If 50 nutrition products did not have EU approval, then how many domestic cosmetic products did not have EU approval?
Ans: 50
Sol:
50-x+30 = 50
=> x = 30
=> y = 30
So, 80-y = 50
Passage - 2
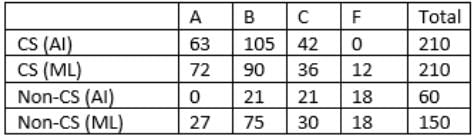
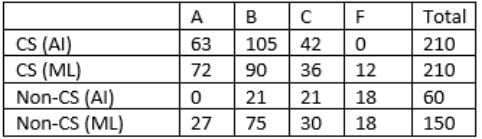
All the first-year students in the computer science (CS) department in a university take both the courses (i) AI and (ii) ML. Students from other departments (non-CS students) can also take one of these two courses, but not both. Students who fail in a course get an F grade; others pass and are awarded A or B or C grades depending on their performance. The following are some additional facts about the number of students who took these two courses this year and the grades they obtained.
- The number of non-CS students who took either AI or ML was equal to the number of CS students.
- The numbers of non-CS students who failed in the two courses were the same and their total is equal to the number of CS students who got a C grade in ML.
- In both the courses, 50% of the students who passed got a B grade. But, while the numbers of students who got A and C grades were the same for AI, they were in the ratio 3 : 2 for ML.
- No CS student failed in AI, while no non-CS student got an A grade in AI.
- The numbers of CS students who got A, B and C grades respectively in AI were in the ratio 3 : 5 : 2, while in ML the ratio was 4 : 5 : 2.
- The ratio of the total number of non-CS students failing in one of the two courses to the number of CS students failing in one of the two courses was 3 : 1.
- 30 students failed in ML.
- The numbers of non-CS students who took AI and ML were in the ratio 2 : 5.
Q1: How many students took AI?
(a) 90
(b) 60
(c) 270
(d) 210
Ans: c
Sol:
From (1) and (2),
Let Non-CS students who took AI & ML = 2x & 5x respectively
Number of CS students = 2x + 5x = 7x, and each of these 7x students took AI and ML.
From (3),
Let the number of non-CS students who failed in the two courses be ‘a’ each. So, a+a = 2a students got C grade in ML.
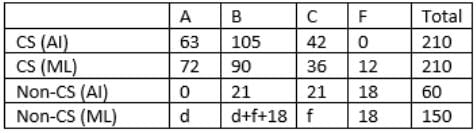
Using (5), (6) and other points, we get the following table:From (7),
2a/(30-a) = 3/1
=> a = 18
=> x = 30
For CS, number of students opting for AI = number of students opting for ML
=> 10b = 30+10a
=> b = 21
From (4), in both the courses, 50% of the students who passed got a B grade.
=> For each course, sum of students who got A and C grade = students who got B grade.
i.e., For AI, 3b+2b+0+b = 5b+c
=> c = b
For ML, 4a+2a+d+f = 5a+e
=> e = a+d+f = d+f+18From table, 2d+2f+36 = 150
=> d+f = 57 ……….(i)
From (4), (4a+d)/(2a+f) = 3/2
=> 6a+3f = 8a+2d
=> 3f-2d = 36 ……….(ii)
Solving (i) and (ii), we get f = 30, d = 27
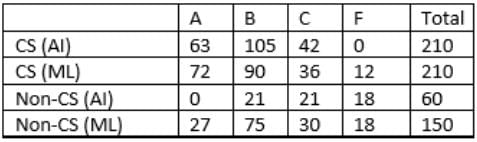
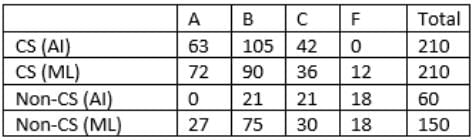
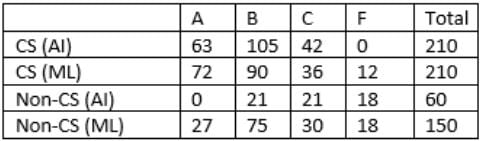
The final table is:
So, 210+60 =270 students took AI.
Q2: How many CS students failed in ML?
Ans: 12
Sol:
From the table, 12 CS students failed in ML.
Q3: How many non-CS students got A grade in ML?
Ans: 27
Sol:
From the table, 27 non-CS students got A grade in ML.
Q4: How many students got A grade in AI?
(a) 63
(b) 99
(c) 84
(d) 42
Ans: a
Sol:
From the table, 63 students got A grade in AI.
Q5: How many non-CS students got B grade in ML?
(a) 165
(b) 75
(c) 25
(d) 90
Ans: b
Sol:
From the table, 75 non-CS students got B grade in ML.
2020
Passage - 1
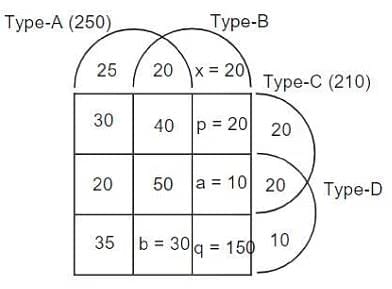
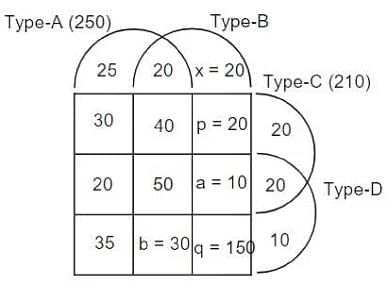
1000 patients currently suffering from a disease were selected to study the effectiveness of treatment of four types of medicines — A, B, C and D. These patients were first randomly assigned into two groups of equal size, called treatment group and control group. The patients in the control group were not treated with any of these medicines; instead they were given a dummy medicine, called placebo, containing only sugar and starch. The following information is known about the patients in the treatment group.
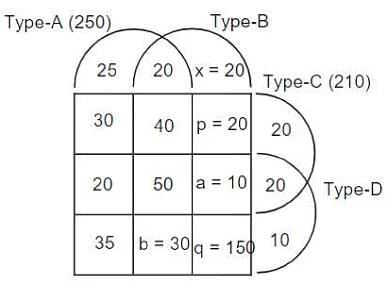
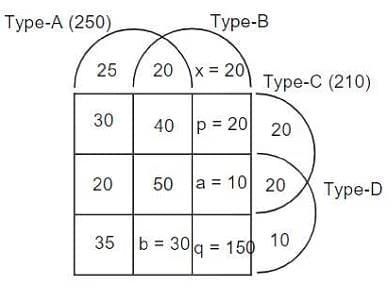
a. A total of 250 patients were treated with type A medicine and a total of 210 patients were treated with type C medicine.
b. 25 patients were treated with type A medicine only. 20 patients were treated with type C medicine only. 10 patients were treated with type D medicine only.
c. 35 patients were treated with type A and type D medicines only. 20 patients were treated with type A and type B medicines only. 30 patients were treated with type A and type C medicines only. 20 patients were treated with type C and type D medicines only.
d. 100 patients were treated with exactly three types of medicines.
e. 40 patients were treated with medicines of types A, B and C, but not with medicines of type D. 20 patients were treated with medicines of types A, C and D, but not with medicines of type B.
f. 50 patients were given all the four types of medicines. 75 patients were treated with exactly one type of medicine
Q1: How many patients were treated with medicine type B?
Ans: 340
Sol: 1000 patients are equally distributed into two groups treatment group and control group. We have some information regarding the effectiveness of medicines A, B, C and D on the treatment group. Let us start filling the data give in the restrictions in a four sets Venn diagram.
75 patients were treated exactly one type of medicine.
∴ 25 + x + 20 + 10 = 75
⇒ x = 20
We have only one unknown in type-A medicine. 220 + b = 250 ⇒ 30
100 patients were treated with exactly three types of medicines. 40 + 20 + 30 + a = 100
⇒ a =10
Now, we have only one unknown in each of the type C and type-D.
⇒ p = 210 - 190 = 20
= 500 - 350 = 150
Q2: The number of patients who were treated with medicine types B, C and D, but not type A was:
Ans: 10
Sol: 1000 patients are equally distributed into two groups treatment group and control group. We have some information regarding the effectiveness of medicines A, B, C and D on the treatment group. Let us start filling the data give in the restrictions in a four sets Venn diagram.
75 patients were treated exactly one type of medicine.
∴ 25 + x + 20 + 10 = 75
⇒ x = 20
We have only one unknown in type-A medicine. 220 + b = 250 ⇒ 30
100 patients were treated with exactly three types of medicines. 40 + 20 + 30 + a = 100
⇒ a =10
Now, we have only one unknown in each of the type C and type-D.
⇒ p = 210 - 190 = 20
= 500 - 350 = 150
Q3: How many patients were treated with medicine types B and D only?
Ans: 150
Sol: 1000 patients are equally distributed into two groups treatment group and control group. We have some information regarding the effectiveness of medicines A, B, C and D on the treatment group. Let us start filling the data give in the restrictions in a four sets Venn diagram.
75 patients were treated exactly one type of medicine.
∴ 25 + x + 20 + 10 = 75
⇒ x = 20
We have only one unknown in type-A medicine. 220 + b = 250 ⇒ 30
100 patients were treated with exactly three types of medicines. 40 + 20 + 30 + a = 100
⇒ a =10
Now, we have only one unknown in each of the type C and type-D.
⇒ p = 210 - 190 = 20
= 500 - 350 = 150
Q4: The number of patients who were treated with medicine type D was:
Ans: 325
Sol: 1000 patients are equally distributed into two groups treatment group and control group. We have some information regarding the effectiveness of medicines A, B, C and D on the treatment group. Let us start filling the data give in the restrictions in a four sets Venn diagram.
75 patients were treated exactly one type of medicine.
∴ 25 + x + 20 + 10 = 75
⇒ x = 20
We have only one unknown in type-A medicine. 220 + b = 250 ⇒ 30
100 patients were treated with exactly three types of medicines. 40 + 20 + 30 + a = 100
⇒ a =10
Now, we have only one unknown in each of the type C and type-D.
⇒ p = 210 - 190 = 20
= 500 - 350 = 150
Passage - 2
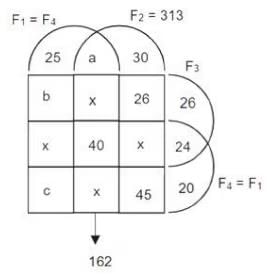
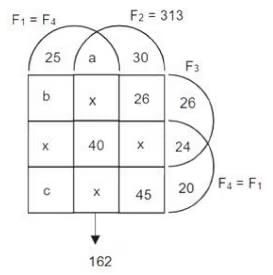
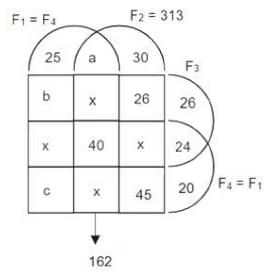
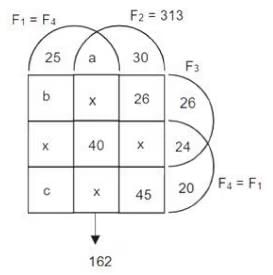
A survey of 600 schools in India was conducted to gather information about their online teaching learning processes (OTLP). The following four facilities were studied.
F1: Own software for OTLP
F2: Trained teachers for OTLP
F3: Training materials for OTLP
F4: All students having Laptops
The following observations were summarized from the survey.
1. 80 schools did not have any of the four facilities – F1, F2, F3, F4.
2. 40 schools had all four facilities.
3. The number of schools with only F1, only F2, only F3, and only F4 was 25, 30, 26 and 20 respectively.
4. The number of schools with exactly three of the facilities was the same irrespective of which three were considered.
5. 313 schools had F2.
6. 26 schools had only F2 and F3 (but neither F1 nor F4).
7. Among the schools having F4, 24 had only F3, and 45 had only F2.
8. 162 schools had both F1 and F2.
9. The number of schools having F1 was the same as the number of schools having F4
Q1: What was the total number of schools having exactly three of the four facilities?
(a) 200
(b) 50
(c) 80
(d) 64
Ans: (a)
Sol: The given information can be represented in the following Venn diagram.
Given, F2 = (a + x + 40 + x) + (30 + 26 + x + 45) = 313
It is also given that F1 and F2 = a + x + 40 + x = 162.
Hence, 30 + 26 + x + 45 = 313 - 162 = 151
Hence, x = 151 - (30 + 26 + 45) = 50
The number of schools that have exactly three facilities = 4x = 200
Q2: What was the number of schools having facilities F2 and F4?
(a) 185
(b) 45
(c) 95
(d) 85
Ans: (a)
Sol: The given information can be represented in the following Venn diagram.
The number of schools having facilities F2 and F4 = 40 + x + 45 + x = 185
Q3: What was the number of schools having only facilities F1 and F3?
Ans: 42
Sol: The given information can be represented in the following Venn diagram.
Only F1 and F3 = b
Given F1 = F4
25 + b + x + c + a + x + 40 + x
= 24 + 20 + x + 45 + 40 + x + x + c
Hence, a + b = 64
it is given that a + x + 40 + x = 162.
As x = 50, a = 22
Hence, only F1 and F3 = b = 64 - 22 = 42
Q4: What was the number of schools having only facilities F1 and F4?
Ans: 20
Sol: The given information can be represented in the following Venn diagram.
Only F1 and F4 = c
Exactly 1 + Exactly 2 + Exactly 3 + Exactly 4 = 600 - 80 = 520
(25+ 30+ 26+ 20)+ Exactly 2 + 200 + 40 = 520
Hence, Exactly 2 = 179 = a + 24 + b + c + 26 + 45
As a = 22 and b = 42, c = only F1 and F4 = 20.
Passage - 3
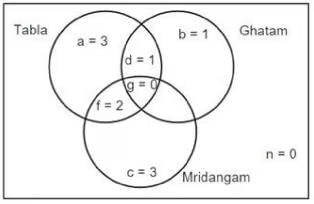
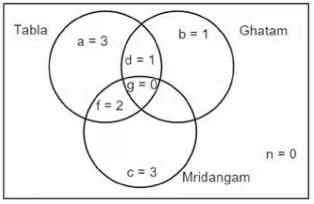
Ten musicians (A, B, C, D, E, F, G, H, I and J) are experts in at least one of the following three percussion instruments: tabla, mridangam, and ghatam. Among them, three are experts in tabla but not in mridangam or ghatam, another three are experts in mridangam but not in tabla or ghatam, and one is an expert in ghatam but not in tabla or mridangam. Further, two are experts in tabla and mridangam but not in ghatam, and one is an expert in tabla and ghatam but not in mridangam.
The following facts are known about these ten musicians.
1. Both A and B are experts in mridangam, but only one of them is also an expert in tabla.
2. D is an expert in both tabla and ghatam.
3. Both F and G are experts in tabla, but only one of them is also an expert in mridangam.
4. Neither I nor J is an expert in tabla.
5. Neither H nor I is an expert in mridangam, but only one of them is an expert in ghatam.
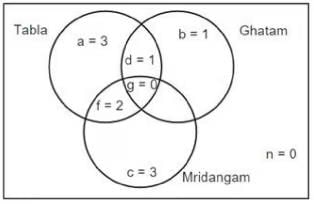
Q1: Who among the following is DEFINITELY an expert in tabla but not in either mridangam or ghatam?
(a) C
(b) H
(c) A
(d) F
Ans: (b)
Sol: The given information can be represented in the following Venn diagram
From (1), one of A and B will be in region c and the other one in region f.
From (2), D is in region d.
From (3), one of F and G will be in region a and the other one in f.
From (4), either both I and J will be in region c or one in region b and the other in region c.
From (5), one of H and I will be in region b and the other in region a.
By combining (4) and (5), I will be in region b, H in region a and J in region c.
Thus, we get the following.
Region a = 3 (F/G, H, C/E), Region b = 1 (I), Region c = 3 (A/B, J, C/E)
Region d = 1 (D), Region f = 2 (B/A, G/F)
H definitely is an expert only in Tabla
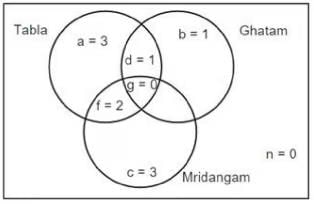
Q2: Which of the following pairs CANNOT have any musician who is an expert in both tabla and mridangam but not in ghatam?
(a) A and B
(b) C and F
(c) C and E
(d) F and G
Ans: (c)
Sol: The given information can be represented in the following Venn diagram
From (1), one of A and B will be in region c and the other one in region f.
From (2), D is in region d.
From (3), one of F and G will be in region a and the other one in f.
From (4), either both I and J will be in region c or one in region b and the other in region c.
From (5), one of H and I will be in region b and the other in region a.
By combining (4) and (5), I will be in region b, H in region a and J in region c.
Thus, we get the following.
Region a = 3 (F/G, H, C/E), Region b = 1 (I), Region c = 3 (A/B, J, C/E)
Region d = 1 (D), Region f = 2 (B/A, G/F)
One of A and B, one of G and F are experts in both tabla and mridangam but not ghatam. Three of the choices has at least one of the above four musicians. But one (C and E) does not have any one of these four. Hence, that is the answer
Q3: Who among the following is DEFINITELY an expert in mridangam but not in either tabla or ghatam?
(a) B
(b) G
(c) J
(d) E
Ans: (c)
Sol: The given information can be represented in the following Venn diagram
From (1), one of A and B will be in region c and the other one in region f.
From (2), D is in region d.
From (3), one of F and G will be in region a and the other one in f.
From (4), either both I and J will be in region c or one in region b and the other in region c.
From (5), one of H and I will be in region b and the other in region a.
By combining (4) and (5), I will be in region b, H in region a and J in region c.
Thus, we get the following.
Region a = 3 (F/G, H, C/E), Region b = 1 (I), Region c = 3 (A/B, J, C/E)
Region d = 1 (D), Region f = 2 (B/A, G/F)
J definitely is an expert only in Mridangam
Q4: If C is an expert in mridangam and F is not, then which are the three musicians who are experts in tabla but not in either mridangam or ghatam?
(a) C, E and G
(b) C, G and H
(c) E, G and H
(d) E, F and H
Ans: (d)
Sol: The given information can be represented in the following Venn diagram
From (1), one of A and B will be in region c and the other one in region f.
From (2), D is in region d.
From (3), one of F and G will be in region a and the other one in f.
From (4), either both I and J will be in region c or one in region b and the other in region c.
From (5), one of H and I will be in region b and the other in region a.
By combining (4) and (5), I will be in region b, H in region a and J in region c.
Thus, we get the following.
Region a = 3 (F/G, H, C/E), Region b = 1 (I), Region c = 3 (A/B, J, C/E)
Region d = 1 (D), Region f = 2 (B/A, G/F)
Given, C is an expert in mridangam but not F. It means F and E are experts only in tabla. Thus, E, F and H will be the experts in tabla but not in mridangam or ghatam.
Passage - 4
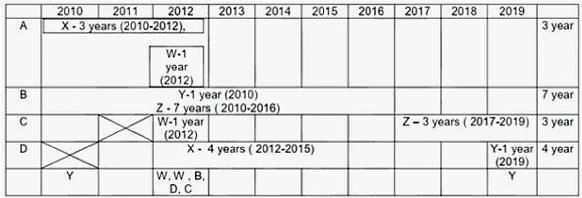
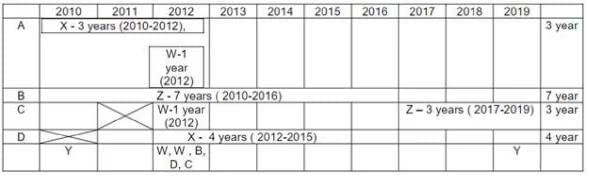
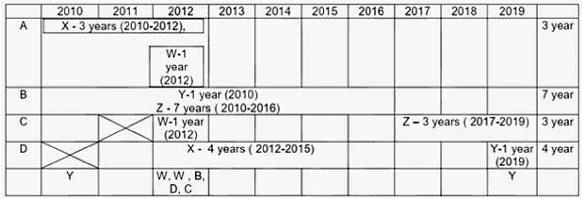
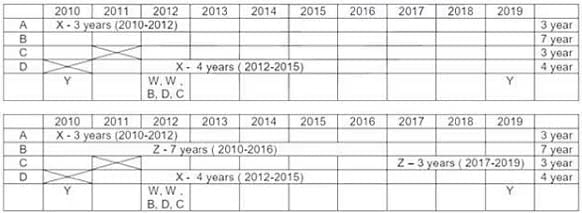
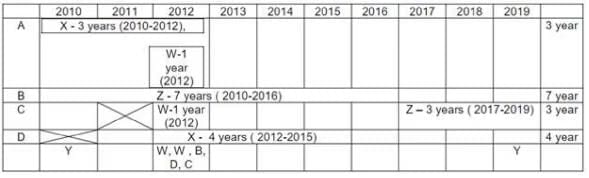
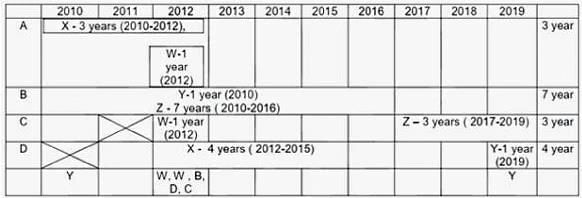
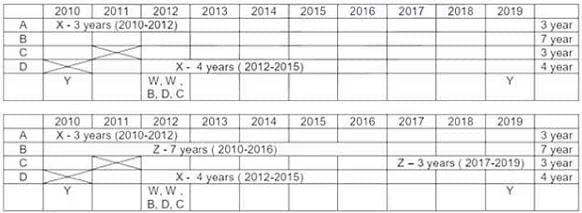
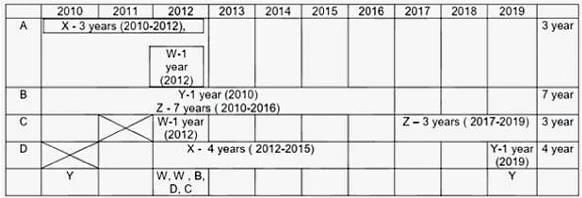
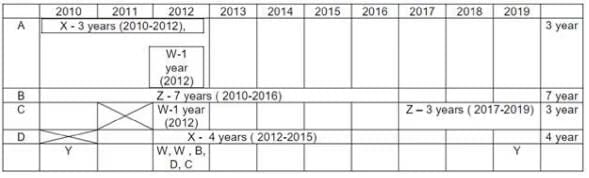
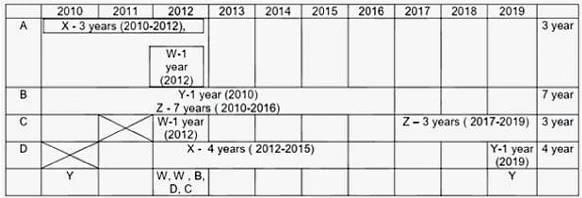
Four institutes, A, B, C, and D, had contracts with four vendors W, X, Y, and Z during the ten calendar years from 2010 to 2019. The contracts were either multi-year contracts running for several consecutive years or single-year contracts. No institute had more than one contract with the same vendor. However, in a calendar year, an institute may have had contracts with multiple vendors, and a vendor may have had contracts with multiple institutes. It is known that over the decade, the institutes each got into two contracts with two of these vendors, and each vendor got into two contracts with two of these institutes.
The following facts are also known about these contracts.
I. Vendor Z had at least one contract in every year.
II. Vendor X had one or more contracts in every year up to 2015, but no contract in any year after that.
III. Vendor Y had contracts in 2010 and 2019. Vendor W had contracts only in 2012.
IV. There were five contracts in 2012.
V. There were exactly four multi-year contracts. Institute B had a 7-year contract, D had a 4- year contract, and A and C had one 3-year contract each. The other four contracts were single-year contracts.
VI. Institute C had one or more contracts in 2012 but did not have any contract in 2011.
VII. Institutes B and D each had exactly one contract in 2012. Institute D did not have any contract in 2010.
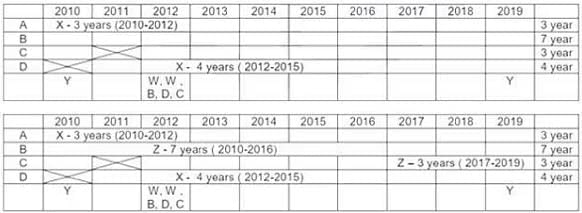
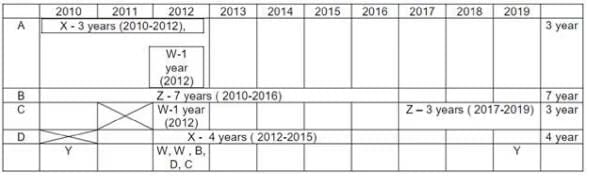
Q1: In which of the following years were there two or more contracts?
(a) 2018
(b) 2017
(c) 2015
(d) 2016
Ans: (c)
Sol: Institutes A, B, C, D Vendors W, X, Y, Z
Contracts Awarded are multiyear Contracts (consecutive years) or single Year Contract.
No institute had more than one contract with the single vendor.
Each Institute → Two contracts → two vendors
Each Vendor → two contracts → two institutes
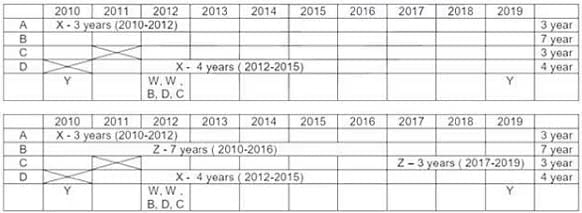
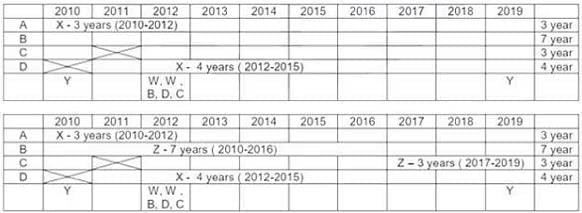
V. Exactly 4 multi year contract (A-3 years, B-7 years, C-3 years, D-4 years). Exactly 4 single year contracts. In total 8 contracts.
I. Vendor Z had at least one contract in ever year. This is only possible if he had both the contracts which are multi years contract. As 7 + 1 = 8 not possible. Only possibility is (7 years + 3 years) or (3 years + 7 years) = 10 years.
II. Vendor X → Six years 2010, 2011, 2012, 2013, 2014, 2015. To have contract for theses six years, only possibility is left with multi years contracts (4 years + 3 years or 3 years + 4 years) with 1 year overlapping contract. PI. Note (3 years + 3 years) is not possible for vendor X as one 3 years is already awarded to vendor Z{(7 years + 3 years ) or (3 years + 7 years) = 10 years}.
So all the 4 multiyear contracts are awarded to Z (3 years, 7 years) & X (3 years, 4 years). So we are left with 4 single year contracts.
III. Vendor Y had contracts in 2010 & 2019. Both of these contracts are single year contracts.
Vendor W had contracts (two contracts) only in year 2012. So both of these are single year contracts.
IV. There are 5 contracts in 2012.
VI. Institute C had one or more contracts in 2012, but no contract in 2011.
VII. Institute B & D each had exactly one contract in 2012. Institute D did not have any contract in 2010.
Out of 5 contracts in 2012 {B, D, W, W and C at least one contract). Hence C has exactly one contract in 2012.
For Vendor X, 4 year contract is with D. It Can vary from (2011-2014) or (2012-2015). No contract can be awarded to him after 2015 (point II). Only possibility for 3 year contract is with A only, as C do not have any contract in 2011. Therefore Vendor X has a 3 year contract with institute A from 2010-2012 & a 4 year contract with institute D from 2012 to 2015 (so as to have one or more contract from 2012 to 2015).
Vendor Z can be allotted contracts with only Institute B & C Only. As vendor Z has at least one contract in every year ( point I) , thus the only possibility left is first 7 year contract with institute B and then 3 year contract with institute C ( as institute C do not have any contract in 2011).
In 2012 there are 5 contracts. Three contracts are already assigned. Remaining two are single year contracts of W in 2012. Also Institute C has at least one contract in 2012. {No institute had more than one contract with the same vendor (initial condition)}. Hence both vendor W 1 years contract cannot be with Institute C. Hence Exactly one contract of vendor W is with institute C. Further, Point VII, Institutes B and D each had exactly one contract in 2012 which is already assigned. Hence second 1 year contract of vendor W is with institute A in 2012 (only possibility).
Institute A has allotted two contracts to 2 vendors {X & W}. Institute C had allotted contracts to two vendors {W & Z}. Hence Vendor Y can have a 1 year contract with only Institute B in 2010, (only possibility left). Hence vendor Y had 1 year contract in 2019 with Institute D (only possibility left).
In 2015 there were two contracts with vendor Z and X
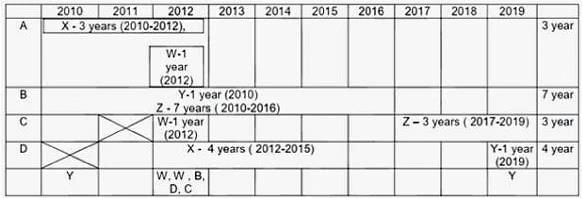
Q2: In how many years during this period was there only one contract?
(a) 4
(b) 2
(c) 3
(d) 5
Ans: (c)
Sol: Institutes A, B, C, D Vendors W, X, Y, Z
Contracts Awarded are multiyear Contracts (consecutive years) or single Year Contract.
No institute had more than one contract with the single vendor.
Each Institute → Two contracts → two vendors
Each Vendor → two contracts → two institutes
V. Exactly 4 multi year contract (A-3 years, B-7 years, C-3 years, D-4 years). Exactly 4 single year contracts. In total 8 contracts.
I. Vendor Z had at least one contract in ever year. This is only possible if he had both the contracts which are multi years contract. As 7 + 1 = 8 not possible. Only possibility is (7 years + 3 years) or (3 years + 7 years) = 10 years.
II. Vendor X → Six years 2010, 2011, 2012, 2013, 2014, 2015. To have contract for theses six years, only possibility is left with multi years contracts (4 years + 3 years or 3 years + 4 years) with 1 year overlapping contract. PI. Note (3 years + 3 years) is not possible for vendor X as one 3 years is already awarded to vendor Z{(7 years + 3 years ) or (3 years + 7 years) = 10 years}.
So all the 4 multiyear contracts are awarded to Z (3 years, 7 years) & X (3 years, 4 years). So we are left with 4 single year contracts.
III. Vendor Y had contracts in 2010 & 2019. Both of these contracts are single year contracts.
Vendor W had contracts (two contracts) only in year 2012. So both of these are single year contracts.
IV. There are 5 contracts in 2012.
VI. Institute C had one or more contracts in 2012, but no contract in 2011.
VII. Institute B & D each had exactly one contract in 2012. Institute D did not have any contract in 2010.
Out of 5 contracts in 2012 {B, D, W, W and C at least one contract). Hence C has exactly one contract in 2012.
For Vendor X, 4 year contract is with D. It Can vary from (2011-2014) or (2012-2015). No contract can be awarded to him after 2015 (point II). Only possibility for 3 year contract is with A only, as C do not have any contract in 2011. Therefore Vendor X has a 3 year contract with institute A from 2010-2012 & a 4 year contract with institute D from 2012 to 2015 (so as to have one or more contract from 2012 to 2015).
Vendor Z can be allotted contracts with only Institute B & C Only. As vendor Z has at least one contract in every year ( point I) , thus the only possibility left is first 7 year contract with institute B and then 3 year contract with institute C ( as institute C do not have any contract in 2011).
In 2012 there are 5 contracts. Three contracts are already assigned. Remaining two are single year contracts of W in 2012. Also Institute C has at least one contract in 2012. {No institute had more than one contract with the same vendor (initial condition)}. Hence both vendor W 1 years contract cannot be with Institute C. Hence Exactly one contract of vendor W is with institute C. Further, Point VII, Institutes B and D each had exactly one contract in 2012 which is already assigned. Hence second 1 year contract of vendor W is with institute A in 2012 (only possibility).
Institute A has allotted two contracts to 2 vendors {X & W}. Institute C had allotted contracts to two vendors {W & Z}. Hence Vendor Y can have a 1 year contract with only Institute B in 2010, (only possibility left). Hence vendor Y had 1 year contract in 2019 with Institute D (only possibility left).
In three years {in 2016 (Z), 2017 (Z), 2018 (Z)} there were only one contract
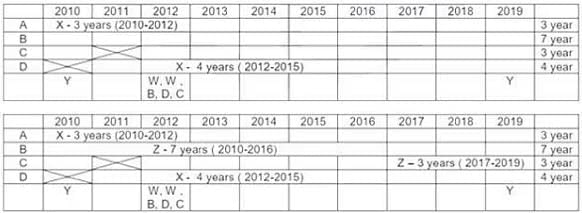
Q3: Which institutes had multiple contracts during the same year?
(a) B and C only
(b) A only
(c) B only
(d) A and B only
Ans: (d)
Sol: Institutes A, B, C, D Vendors W, X, Y, Z
Contracts Awarded are multiyear Contracts (consecutive years) or single Year Contract.
No institute had more than one contract with the single vendor.
Each Institute → Two contracts → two vendors
Each Vendor → two contracts → two institutes
V. Exactly 4 multi year contract (A-3 years, B-7 years, C-3 years, D-4 years). Exactly 4 single year contracts. In total 8 contracts.
I. Vendor Z had at least one contract in ever year. This is only possible if he had both the contracts which are multi years contract. As 7 + 1 = 8 not possible. Only possibility is (7 years + 3 years) or (3 years + 7 years) = 10 years.
II. Vendor X → Six years 2010, 2011, 2012, 2013, 2014, 2015. To have contract for theses six years, only possibility is left with multi years contracts (4 years + 3 years or 3 years + 4 years) with 1 year overlapping contract. PI. Note (3 years + 3 years) is not possible for vendor X as one 3 years is already awarded to vendor Z{(7 years + 3 years ) or (3 years + 7 years) = 10 years}.
So all the 4 multiyear contracts are awarded to Z (3 years, 7 years) & X (3 years, 4 years). So we are left with 4 single year contracts.
III. Vendor Y had contracts in 2010 & 2019. Both of these contracts are single year contracts.
Vendor W had contracts (two contracts) only in year 2012. So both of these are single year contracts.
IV. There are 5 contracts in 2012.
VI. Institute C had one or more contracts in 2012, but no contract in 2011.
VII. Institute B & D each had exactly one contract in 2012. Institute D did not have any contract in 2010.
Out of 5 contracts in 2012 {B, D, W, W and C at least one contract). Hence C has exactly one contract in 2012.
For Vendor X, 4 year contract is with D. It Can vary from (2011-2014) or (2012-2015). No contract can be awarded to him after 2015 (point II). Only possibility for 3 year contract is with A only, as C do not have any contract in 2011. Therefore Vendor X has a 3 year contract with institute A from 2010-2012 & a 4 year contract with institute D from 2012 to 2015 (so as to have one or more contract from 2012 to 2015).
Vendor Z can be allotted contracts with only Institute B & C Only. As vendor Z has at least one contract in every year ( point I) , thus the only possibility left is first 7 year contract with institute B and then 3 year contract with institute C ( as institute C do not have any contract in 2011).
In 2012 there are 5 contracts. Three contracts are already assigned. Remaining two are single year contracts of W in 2012. Also Institute C has at least one contract in 2012. {No institute had more than one contract with the same vendor (initial condition)}. Hence both vendor W 1 years contract cannot be with Institute C. Hence Exactly one contract of vendor W is with institute C. Further, Point VII, Institutes B and D each had exactly one contract in 2012 which is already assigned. Hence second 1 year contract of vendor W is with institute A in 2012 (only possibility).
Institute A has allotted two contracts to 2 vendors {X & W}. Institute C had allotted contracts to two vendors {W & Z}. Hence Vendor Y can have a 1 year contract with only Institute B in 2010, (only possibility left). Hence vendor Y had 1 year contract in 2019 with Institute D (only possibility left).
A → (X & W) in 2012, B → (Z & Y) in 2010
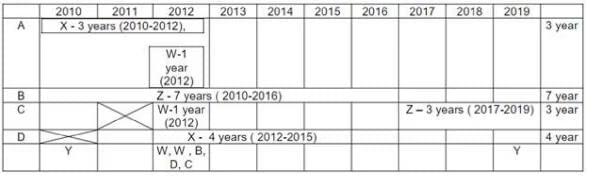
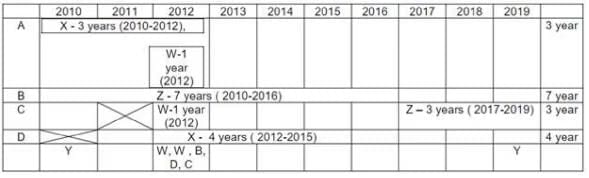
Q4: Which of the following is true?
(a) D had a contract with Y in 2019
(b) D had a contract with X in 2011
(c) B had a contract with Y in 2019
(d) B had a contract with Z in 2017
Ans: (a)
Sol: Institutes A, B, C, D Vendors W, X, Y, Z
Contracts Awarded are multiyear Contracts (consecutive years) or single Year Contract.
No institute had more than one contract with the single vendor.
Each Institute → Two contracts → two vendors
Each Vendor → two contracts → two institutes
V. Exactly 4 multi year contract (A-3 years, B-7 years, C-3 years, D-4 years). Exactly 4 single year contracts. In total 8 contracts.
I. Vendor Z had at least one contract in ever year. This is only possible if he had both the contracts which are multi years contract. As 7 + 1 = 8 not possible. Only possibility is (7 years + 3 years) or (3 years + 7 years) = 10 years.
II. Vendor X → Six years 2010, 2011, 2012, 2013, 2014, 2015. To have contract for theses six years, only possibility is left with multi years contracts (4 years + 3 years or 3 years + 4 years) with 1 year overlapping contract. PI. Note (3 years + 3 years) is not possible for vendor X as one 3 years is already awarded to vendor Z{(7 years + 3 years) or (3 years + 7 years) = 10 years}.
So all the 4 multiyear contracts are awarded to Z (3 years, 7 years) & X (3 years, 4 years). So we are left with 4 single year contracts.
III. Vendor Y had contracts in 2010 & 2019. Both of these contracts are single year contracts.
Vendor W had contracts (two contracts) only in year 2012. So both of these are single year contracts.
IV. There are 5 contracts in 2012.
VI. Institute C had one or more contracts in 2012, but no contract in 2011.
VII. Institute B & D each had exactly one contract in 2012. Institute D did not have any contract in 2010.
Out of 5 contracts in 2012 {B, D, W, W and C at least one contract). Hence C has exactly one contract in 2012.
For Vendor X, 4 year contract is with D. It Can vary from (2011-2014) or (2012-2015). No contract can be awarded to him after 2015 (point II). Only possibility for 3 year contract is with A only, as C do not have any contract in 2011. Therefore Vendor X has a 3 year contract with institute A from 2010-2012 & a 4 year contract with institute D from 2012 to 2015 (so as to have one or more contract from 2012 to 2015).
Vendor Z can be allotted contracts with only Institute B & C Only. As vendor Z has at least one contract in every year ( point I) , thus the only possibility left is first 7 year contract with institute B and then 3 year contract with institute C ( as institute C do not have any contract in 2011).
In 2012 there are 5 contracts. Three contracts are already assigned. Remaining two are single year contracts of W in 2012. Also Institute C has at least one contract in 2012. {No institute had more than one contract with the same vendor (initial condition)}. Hence both vendor W 1 years contract cannot be with Institute C. Hence Exactly one contract of vendor W is with institute C. Further, Point VII, Institutes B and D each had exactly one contract in 2012 which is already assigned. Hence second 1 year contract of vendor W is with institute A in 2012 (only possibility).
Institute A has allotted two contracts to 2 vendors {X & W}. Institute C had allotted contracts to two vendors {W & Z}. Hence Vendor Y can have a 1 year contract with only Institute B in 2010, (only possibility left). Hence vendor Y had 1 year contract in 2019 with Institute D (only possibility left).
D had a contract with Y in 2019
Q5: What BEST can be concluded about the number of contracts in 2010?
(a) exactly 4
(b) at least 4
(c) exactly 3
(d) at least 3
Ans: (c)
Sol: Institutes A, B, C, D Vendors W, X, Y, Z
Contracts Awarded are multiyear Contracts (consecutive years) or single Year Contract.
No institute had more than one contract with the single vendor.
Each Institute → Two contracts → two vendors
Each Vendor → two contracts → two institutes
V. Exactly 4 multi year contract (A-3 years, B-7 years, C-3 years, D-4 years). Exactly 4 single year contracts. In total 8 contracts.
I. Vendor Z had at least one contract in ever year. This is only possible if he had both the contracts which are multi years contract. As 7 + 1 = 8 not possible. Only possibility is (7 years + 3 years) or (3 years + 7 years) = 10 years.
II. Vendor X → Six years 2010, 2011, 2012, 2013, 2014, 2015. To have contract for theses six years, only possibility is left with multi years contracts (4 years + 3 years or 3 years + 4 years) with 1 year overlapping contract. PI. Note (3 years + 3 years) is not possible for vendor X as one 3 years is already awarded to vendor Z{(7 years + 3 years) or (3 years + 7 years) = 10 years}.
So all the 4 multiyear contracts are awarded to Z (3 years, 7 years) & X (3 years, 4 years). So we are left with 4 single year contracts.
III. Vendor Y had contracts in 2010 & 2019. Both of these contracts are single year contracts.
Vendor W had contracts (two contracts) only in year 2012. So both of these are single year contracts.
IV. There are 5 contracts in 2012.
VI. Institute C had one or more contracts in 2012, but no contract in 2011.
VII. Institute B & D each had exactly one contract in 2012. Institute D did not have any contract in 2010.
Out of 5 contracts in 2012 {B, D, W, W and C at least one contract). Hence C has exactly one contract in 2012.
For Vendor X, 4 year contract is with D. It Can vary from (2011-2014) or (2012-2015). No contract can be awarded to him after 2015 (point II). Only possibility for 3 year contract is with A only, as C do not have any contract in 2011. Therefore Vendor X has a 3 year contract with institute A from 2010-2012 & a 4 year contract with institute D from 2012 to 2015 (so as to have one or more contract from 2012 to 2015).
Vendor Z can be allotted contracts with only Institute B & C Only. As vendor Z has at least one contract in every year ( point I) , thus the only possibility left is first 7 year contract with institute B and then 3 year contract with institute C ( as institute C do not have any contract in 2011).
In 2012 there are 5 contracts. Three contracts are already assigned. Remaining two are single year contracts of W in 2012. Also Institute C has at least one contract in 2012. {No institute had more than one contract with the same vendor (initial condition)}. Hence both vendor W 1 years contract cannot be with Institute C. Hence Exactly one contract of vendor W is with institute C. Further, Point VII, Institutes B and D each had exactly one contract in 2012 which is already assigned. Hence second 1 year contract of vendor W is with institute A in 2012 (only possibility).
Institute A has allotted two contracts to 2 vendors {X & W}. Institute C had allotted contracts to two vendors {W & Z}. Hence Vendor Y can have a 1 year contract with only Institute B in 2010, (only possibility left). Hence vendor Y had 1 year contract in 2019 with Institute D (only possibility left).
In 2010 {(A-X), (B-Z), (B-Y)} exactly three contracts.
Q6: Which institutes and vendors had more than one contracts in any year?
(a) A, D, W, and Z
(b) B, W, X, and Z
(c) B, D, W, and X
(d) A, B, W, and X
Ans: (d)
Sol: Institutes A, B, C, D Vendors W, X, Y, Z
Contracts Awarded are multiyear Contracts (consecutive years) or single Year Contract.
No institute had more than one contract with the single vendor.
Each Institute → Two contracts → two vendors
Each Vendor → two contracts → two institutes
V. Exactly 4 multi year contract (A-3 years, B-7 years, C-3 years, D-4 years). Exactly 4 single year contracts. In total 8 contracts.
I. Vendor Z had at least one contract in ever year. This is only possible if he had both the contracts which are multi years contract. As 7 + 1 = 8 not possible. Only possibility is (7 years + 3 years) or (3 years + 7 years) = 10 years.
II. Vendor X → Six years 2010, 2011, 2012, 2013, 2014, 2015. To have contract for theses six years, only possibility is left with multi years contracts (4 years + 3 years or 3 years + 4 years) with 1 year overlapping contract. PI. Note (3 years + 3 years) is not possible for vendor X as one 3 years is already awarded to vendor Z{(7 years + 3 years) or (3 years + 7 years) = 10 years}.
So all the 4 multiyear contracts are awarded to Z (3 years, 7 years) & X (3 years, 4 years). So we are left with 4 single year contracts.
III. Vendor Y had contracts in 2010 & 2019. Both of these contracts are single year contracts.
Vendor W had contracts (two contracts) only in year 2012. So both of these are single year contracts.
IV. There are 5 contracts in 2012.
VI. Institute C had one or more contracts in 2012, but no contract in 2011.
VII. Institute B & D each had exactly one contract in 2012. Institute D did not have any contract in 2010.
Out of 5 contracts in 2012 {B, D, W, W and C at least one contract). Hence C has exactly one contract in 2012.
For Vendor X, 4 year contract is with D. It Can vary from (2011-2014) or (2012-2015). No contract can be awarded to him after 2015 (point II). Only possibility for 3 year contract is with A only, as C do not have any contract in 2011. Therefore Vendor X has a 3 year contract with institute A from 2010-2012 & a 4 year contract with institute D from 2012 to 2015 (so as to have one or more contract from 2012 to 2015).
Vendor Z can be allotted contracts with only Institute B & C Only. As vendor Z has at least one contract in every year ( point I) , thus the only possibility left is first 7 year contract with institute B and then 3 year contract with institute C ( as institute C do not have any contract in 2011).
In 2012 there are 5 contracts. Three contracts are already assigned. Remaining two are single year contracts of W in 2012. Also Institute C has at least one contract in 2012. {No institute had more than one contract with the same vendor (initial condition)}. Hence both vendor W 1 years contract cannot be with Institute C. Hence Exactly one contract of vendor W is with institute C. Further, Point VII, Institutes B and D each had exactly one contract in 2012 which is already assigned. Hence second 1 year contract of vendor W is with institute A in 2012 (only possibility).
Institute A has allotted two contracts to 2 vendors {X & W}. Institute C had allotted contracts to two vendors {W & Z}. Hence Vendor Y can have a 1 year contract with only Institute B in 2010, (only possibility left). Hence vendor Y had 1 year contract in 2019 with Institute D (only possibility left).
Institutes { A → 2012, B → 2010}, Vendors { W → 2012 X → 2012}
|
77 videos|180 docs|96 tests
|
FAQs on Venn Diagrams & Set Theory CAT Previous Year Questions with Answer PDF
| 1. What is a Venn diagram and how is it used in CAT exams? |  |
| 2. How can Venn diagrams be used to solve CAT exam questions on set theory? |  |
| 3. What are the key elements of a Venn diagram in the context of CAT exams? |  |
| 4. Can Venn diagrams be used to solve complex CAT exam questions involving multiple sets? |  |
| 5. Are there any limitations or drawbacks of using Venn diagrams to solve CAT exam questions? |  |