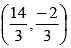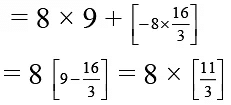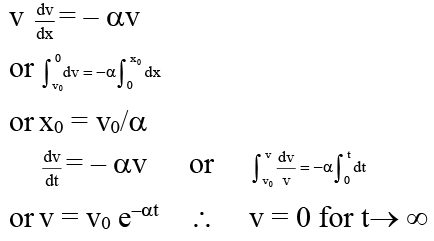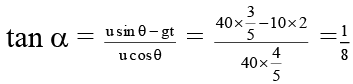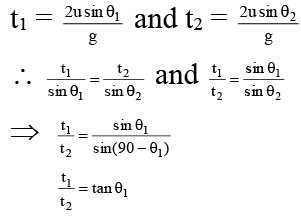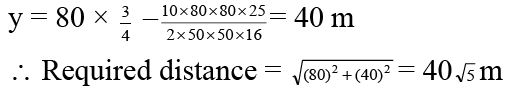JEE Advanced (One or More Correct Option): Motion | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. A body moves so that it follows the following relation dt/dv = –v² + 2v – 1 where v is speed in m/s and t is time in second. If at t = 0, v = 0 then
(a) terminal velocity is 1 m/s
(b) the magnitude of initial acceleration is 1 m/s²
(c) instantaneous speed is v = -1/1 + t
(d) the speed is 1.5 m/s when acceleration is one fourth of its initial value

Correct Answer is Option (a, b and d)

dv/dt = – v² + 2v – 1
Terminal velocity is attained when a = 0
⇒ dv/dt = 0

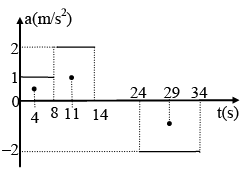
Q.2. A particle moves in a straight line with an a–t curve shown in figure. The initial displacement and velocity are zero.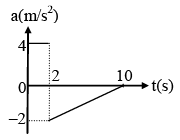

(a) The time at which the particle comes to rest again is 10 sec.
(b) Velocity of particle at t = 2 sec is 8 m/s.
(c) Distance travelled by particle before coming to rest is 29.36 m.
(d) Displacement of the particle before coming to rest is 29.36 m.

Correct Answer is Option (a, b c and d)

Area under a-t curve:
Δv = Area 1 = 2 × 4 = 8
v - u = 8
v = u + 8 = 0 + 8 = 8 m/s
v' - v = Area 2 = (1/2 x 8x2)= – 8 m/s
v' = v – 8 = 8 – 8 = 0
Final velocity is zero at t = 10 sec
Displacement: Can be directly calculated from a–t cure without using v–t curve.
ΔS = u₀t₀ + (area under a-t curve) (t₀ - t_c)
Where ΔS = displacement
u₀ = initial velocity
t₀ = total time

t_c = Abscissa of centroid of corresponding area

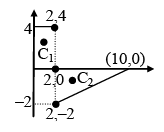
Centroid of area 1: C₁ = (1,2)
Centroid of area 2 : C₂ =

= 8 × 3.666 = 8 × 3.67
ΔS = 29.36 m

Q.3. A train travels between two of its station stops with the acceleration schedule shown. Δt is the time interval during which train breaks to stop.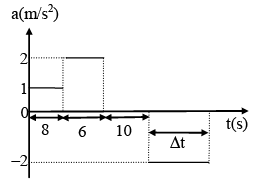

(a) Δt = 10 sec
(b) Distance between two stations is 416 m
(c) Δt = 15 sec
(d) Distance between two stations is 510 m

Correct Answer is Option (a and b)

Area under graph gives change in velocity
Train starts from rest and comes to rest
Therefore, Positive area = negative area
8 × 1 + 6 × 2 = 2 × Δt
8 + 12 = 2Δt
Δt = 20 = 10 sec
Displacement & distance are equal in this case displacement can be directly calculated from at curve without using v-t curve as follows
ΔS = ut₀ + (area under a-t curve) (t₀ - t_c)
Where u → initial velocity
t₀ → total time
t_c → abscissa of centroid of corresponding area

Δs = 8 [34 - 4] + 12 [34 - 11] + (-20) [34 - 29]
= 8  × 30 + 12 × 23 - 20 × 5
= 240 + 276 – 100
= 516 – 100
Δs = 416 m

Q.4. A particle moves with an initial velocity v₀ and retardation αv, where v is its velocity at any time t
(a) The particle will cover a total distance v₀/α
(b) The particle will come to rest after a time 1 /α
(c) The particle will continue to move for a very long time
(d) The velocity of the particle will become v₀/2 after a time 1/α

Correct Answer is Option (a and c)

Q.5. In the figure is shown the position of a particle moving on the x-axis as a function of time. Then -

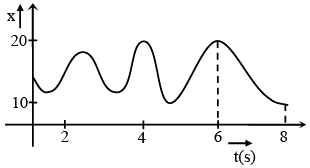
(a) the particle has come to rest for 6 times
(b) the maximum speed is at t = 6 s
(c) the velocity remain positive for t = 0 to t = 6s
(d) the average velocity for the total period shown is negative.

Correct Answer is Option (a and d)
In x - t graph at maxima and minima. dt/dx = 0, hence particle comes to rest for 6 times and average velocity for total period is negative.

Q.6. A projectile is projected with a speed of 40m/s at an angle θ with horizontal such that
tan θ = 3/4. After 2 sec, the projectile is moving with speed v at an angle α with horizontal then, (g = 10 m/s²)
(a) tan α = 1/8
(b) cot α = 1/8
(c) v = 32.25 m/s
(d) 32 m/s

Correct Answer is Option (a and c)

and v cos α = u cos θ
∴ v x 8/√65 = 40 x 4/5 = 32.25 m/s

Q.7. Path of three projectiles are shown. If T₁, T₂ and T₃ are time of flights and ignoring air resistances –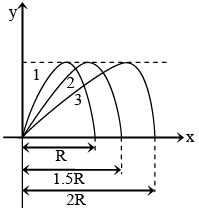

(a) T₁ > T₃
(b) T₁ < T₃

(c) 
(d) T₁ = T₂ = T₃

Correct Answer is Option (c and d)
As maximum heights are same therefore their time of flights will be same.

Q.8. Two particles are projected from the same point with the same speed, at different angles θ₁ and θ₂ to the horizontal.  Their times of flight are t₁ and t₂ and they have the same horizontal range.  Then-
(a)  t₁/t₂ = tan θ₁
(b)  t₁/t₂ = tan θ₂
(c)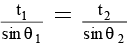 
(d) θ₁ + θ₂ = 90º

Correct Answer is Option (A, c and d)
For same range, θ₁ and θ₂.
θ₂ = (90 - θ₁) ⇒ θ₁ + θ₂ = 90º

Q.9. A body is thrown from a point with speed 50 m/s and an angle 37º with horizontal in time t it has moved a horizontal distance of 80 m, then its distance from point of projection is d, then – (g = 10 m/s²)
(a) d = 40 m
(b) 40√5 m
(c) t = 2 sec
(d) t = 2.67 sec  

Correct Answer is Option (a and b)

Q.10. A particle is projected with a speed v and an angle θ with horizontal. Choose the correct statements -
(a) Speed of the particle is zero at highest point.
(b) Speed of the particle is minimum at highest point.
(c) Acceleration of particle throughout the motion is constant.
(d) Acceleration of particle varies with time.

Correct Answer is Option (b and c)
At highest point, speed is not zero and it is equal to u cos θ.
Acceleration is constant.