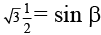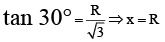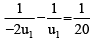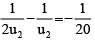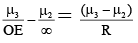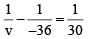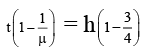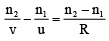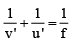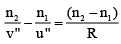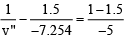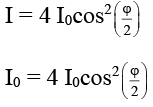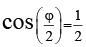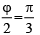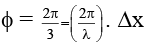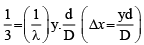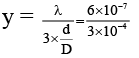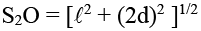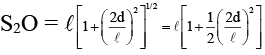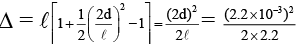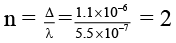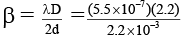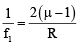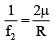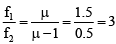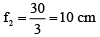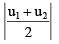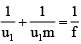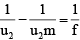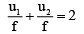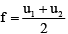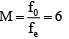Integer Answer Type Questions for JEE: Ray & Wave Optics | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. A ray is incident normally on a right angle prism whose μ is √3 and prism angle a = 30°, after crossing prism ray passes through glass sphere. It strikes the glass sphere of radius R at R/2 distance from principal axis, as shown in figure. Sphere is half polished. Find the angle of deviation of incident ray.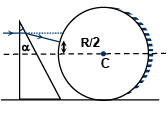

Ans. 180^o
μ sin 30° = sin b

β = 60°
δ = 30°
Point P where it strikes is R / √3

⇒ Ray strikes normal to the spherical surface. It retraces the path.
∴ Angle of deviation = 180°

Q.2. A concave mirror has a focal length 20 cm. The distance between the two positions of the object for which the image size is double of the object size is

Ans. 20 cm
For real image u = – u₁, v = –2u₁ f = 20 cm
Substituting in ,
We get
or u₁ = 30 cm
For virtual image
u = –u₂,  v = 2u₂ f = – 20 cm  
∴
or u₂ = 10 cm
∴ Distance between two positions of the object are u₁ – u₂ or 30 cm – 10 cm = 20 cm

Q.3. A light ray is incident on an irregular shaped slab of refractive index √2 at an angle of 45° with the normal on the incline face as shown in the figure.  The ray finally emerges from the curved surface in the medium of refractive index m = 1.514 and passes through point E.  If the radius of curved surface is equal to 0.4 m, find the distance OE correct upto two decimal places.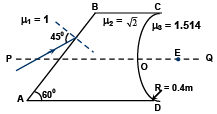

Ans. 6.06 m
OE = 6.06 m
Using Snell’s law
μ₁ sin 45° = μ₂ sin θ θ = 30°.  
i.e. ray moves parallel to axis

OE = 6.056 m » 6.06 m

Q.4. The image of the object O, shown in the figure, is formed at the bottom of the tank filled with water. Using the values given in the figure, calculate the value of h, i.e. the water level in the tank.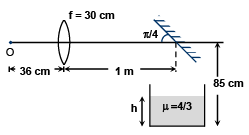

Ans. 20 cm
h = 20 cm.
For the lens

∴ v = 180 cm
This acts as an (virtual) object for the mirror which forms its image at a distance of 80 cm from it (in the absence of water tray).
The water tray shifts the image by
∴ h/4 + 80 = 85 cm
⇒ h = 20 cm.

Q.5. A cylindrical glass rod has its two coaxial ends of spherical form bulging outward. The front end has a radius of curvature 5 cm and the back end which is silvered has a radius of curvature 8 cm. The thickness of the rod along the axis is 10 cm. Calculate the position of the image of a point object at the axis 50 cm from the front face  (_an_g= 1.5).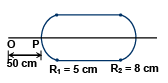

Ans. 4.27 m
Using the formula for refraction through a spherical surface

At the point P, we have, u = - 50 cm, R = 5 cm, n₁ = 1, n₂ = 1.5
Hence,  or v  = +18.75cm
This gives the position of image I₁ w.r.t. pole P.
The silvered surface will act as a concave mirror of radius of curvature R = 8 cm and therefore focal length = 4 cm. The image formed by the first surface will act as an object for second reflecting surface.
The distance of image I₁ from second surface = u'
where u' = -10 + 18.75 = + 8.75 cm
This image will act as a virtual object for mirror since the image is behind the mirror. Applying the formula for the mirror

Here, u' = 8.75 cm, f = -4 cm, hence
 or,  v' = -2.746 cm
This gives the position of image I₂. Now this real image will act as a real object for the front surface where again refraction will take place.
Now, |u''|= 10 - 2.746 = 7.254 cm
∴ u'' = -7.254 cm, R = -5 cm, n₁ = 1.5, n₂ = 1
Applying formula of refraction at spherical surface,

or,
or  or  v” = -9.365 cm
i.e. final image is virtual and appears to originate from a point 9.365 cm behind the front surface.

Q.6. In Young’s double slit experiment 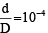 (d = distance between slits, D = distance of screen from the slits). At a point P on the screen resulting intensity is equal to the intensity due to individual slit I₀. Then the distance of point P from the central maximum is (λ = 6000 Å) 

Ans. 2 mm

∴
or
or
or
∴
= 2 × 10^–3 m = 2 mm

Q.7. Two coherent light sources emit light of wavelength 550 nm which produce an interference pattern on a screen. The sources are 2.2 mm apart and 2.2m from the screen. Determine whether the interference at the point O is constructive or destructive. Calculate the fringe width.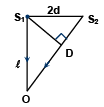

Ans. 0.55 mm
The path difference at O is given by
Δ = S₂O - S₁O
From figure
∴
Now,
= 1.1 x 10^-6 m
The difference will be constructive if path difference is an integral multiples of wavelength
i.e., n = 1, 2, 3 . . . . .

Fringe width,

= 5.5 x 10^-4 m = 0.55 mm.

Q.8. When the plane surface of a plano-convex lens of refractive index 1.5 is silvered, it behaves like a concave mirror with f = 30 cm. When its convex surface is silvered, it will behave like a concave mirror of focal length

Ans. 10 cm
When the plane surface is silvered,

When the convex surface is silvered,

∴
or

Q.9. When an object is at distances of u₁ and u₂ from the poles of a concave mirror, images of the same size are formed. The focal length of the mirror is

Ans. 
One image will be real and the other will be virtual. Since they are of the same size, one will have magnification m and the other -m.

or
and
or

⇒  or

Q.10. A telescope, when in normal adjustment, has a magnifying power of 6 and the objective and eye-piece are 14 cm apart. The focal lengths of the eye-piece and the objective, respectively, are

Ans. 2 cm and 12 cm
Let f_e and f₀ be the focal lengths of the eye-piece and the objective, respectively.
In normal adjustment,
f₀ + f_e = 14 ...(1)
and
f₀ = 6f_e ...(2)
Solving Eqs. (1) and (2), we get
⇒ f_e = 2 cm and f₀ = 12 cm