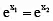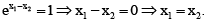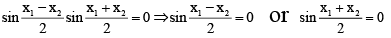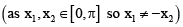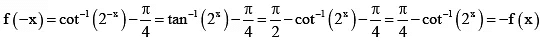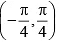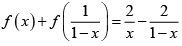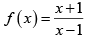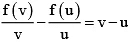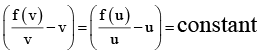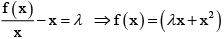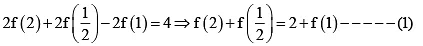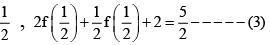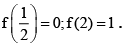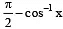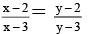JEE Advanced (One or More Correct Option): Sets, Relation & Functions | Chapter-wise Tests for JEE Main & Advanced PDF Download

Clear all your JEE doubts with EduRev Join for Free

Join for Free

Q.1. Which of the following defines a one-one function?
(a)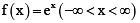
(b)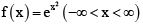
(c)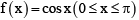
(d)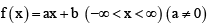

Correct Answer is options (a, c, d)
If f(x) = e^x then  f(x₁) = f(x₂)
⇒
⇒
Thus e^x is one-one.  If f(x) = cos x then, f(x₁) = f(x₂)
⇒ cos x₁ - cos x₂= 0

⇒ x₁ = x₂ 
Thus cos x is one-one. If f(x) = ax + b then f(x₁) = f(x₂)
⇒ ax₁ + b = ax₂ + b
⇒ a(x₁ – x₂) = 0
⇒ x₁ = x₂, as a  ≠ 0 .
Thus ax + b is one-one.
 Hence f is not 1-1.

Q.2. Which of the following functions f : R → R are bijective
(a)  f ( x) = x sin x
(b) f ( x) = x- sin² x
(c)  f ( x) = x+ √x²
(d) f ( x) = - x + cos² x

Correct Answer is options (b, d)
(A) f is not one-one as f cuts x axis twice in (0,2π] If fact f is continuous and achieves every real number infinite times.
(B)  f is monotone as f '( x) = 1 - sin 2 x ≥ 0 ∀ x
 and f is continuous
Hence f is bijective.
(C)  is not one-one as f is a constant function for x ≤ 0
(D) f is monotone as f '(x) ≤ 0 ∀x and as in (B) f is bijective.

Q.3. Let the function f : R → ( 0,π) be defined by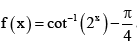
Then
(a) f is odd
(b) f is even
(c) range of f is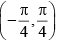
(d) range of f is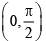

Correct Answer is options (a, c)

Thus f is odd.
Further 2^x ranges from 0 to ∞. The range of cot^-1(2^x) is .
Hence range of f is

Q.4. Let S = {1, 2, 3, .....,n} and f n be the no. of those subsets of S which do not contain consecutive elements of S, then
(a)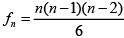
(b)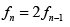  
(c)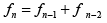
(d) f₄ = 8

Correct Answer is options (c, d)
Let n = 4 , then the subsets of  {1, 2, 3, 4} which do not contain consecutive elements of this set and
Ф ,{1},{2},{3},{4},{1, 3},{1, 4},{2, 4}
f₄ = 8 similarly f = 3,f₃ = 5

Q.5. Let f : R - {0,1} → R satisfying 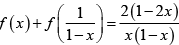 then
(a)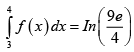
(b) the graph of y = f ( x ) crosses x-axis at x = -1
(c) f ( 2) +f (3)= 5
(d) f ( 2) +f (3)= 6

Correct Answer is options (a, b, c)

Replacing x by 1/1-x and by (1 - 1/x) in equation (1) one by one and on solving, we get

Q.6. If a function satisfies (x - y)f (x + y)-(x + y)f (x - y) = 2(x²y - y³)∀ x, y ∈ R andf (1) = 2 , then
(a) f(x) must be polynomial function
(b) f(3) = 12
(c) f(0) = 0
(d) f(x) may not be differentiable

Correct Answer is options (a, b, c)
(x-y)f (x+ y)-(x + y)f (x -y) = 2y(x -y(x + y))
Let x - t = u; x + y = v
uf ( v ) - vf (u ) = 2uv ( v - u )


Let
f (1) = 2
λ+1 = 2
⇒ λ = 1

Q.7. If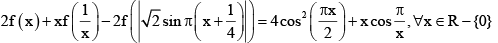  

then which of the following statement(s) is/are true?
(a)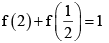
(b) f ( 2) + f (1)= 0
(c)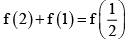
(d)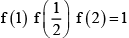

Correct Answer is options (a, b, c)
Replace x by 2,
Replace x by 1, f (1) = -1 - - - - - (2)
Replace x by
Solve (1) & (3)
⇒

Q.8. If f(x) = sin{[x + 5] + {x – {x –{x}}} for x ∈ 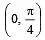, is invertible, where {.} and [.] represent fractional part and greatest integer functions respectively, then f^–1(x) is
(a) sin^–1x
(b)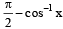
(c) sin^–1{x}
(d) cos^–1{x}

Correct Answer is options (a, b, c)
Θ {[x + 5] + {x – {x – {x}}}}
= {[x + 5] + {x – {[x]}}
= {[x + 5] + {x}} = {{x}} = {x}
So, f(x) = sin{x} for x ∈
so f(x) = sinx
so f^–1(x) = sin^–1(x)
= sin^–1{x}
=

Q.9. The integer 'n' for which n² + 19n + 92 is a perfect square
(a) –8
(b) 8
(c) –11
(d) 11

Correct Answer is options (a, c)
n² + 19n + 92 = x²
⇒ (n² + 19n + 92) = 4x²
⇒ (2n + 19)2 + 7 = 4x²
⇒ 4x² – 7 must be square of integer
Let 4x² – 7 = k²
So 4x² – k² = 7
⇒ (2x – k)(2x + k) = 7
from above ⇒ x = 2
(2n + 19)² + 7 = 16
⇒ (2n + 19)² = 9
⇒ n = –8 or –11

Q.10. Let A = R – {3}, B = R –{1}. Let f : A → B be defined by f(x) = x - 2 / x - 3 . Then
(a) f is bijective
(b) f is one-one
(c) f is onto
(d) one-to-one but not onto

Correct Answer is options (a, b, c)
Let x, y ∈ A be such that f (x) = f(y)
⇔
⇔ xy –3x – 2y + 6 = xy –3y –2x + 6
⇔ –2y + 3y = 3x –2x Û x = y
Hence f is one-one
Let y ∈ B, we want to get x ∈ A such that f(x) = y, i.e., x - 2 / x - 3 = y. Cross multiplying and Solving, we obtain .
Hence f is onto and also bijective.