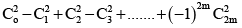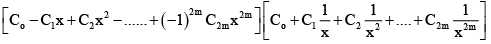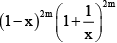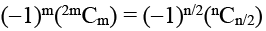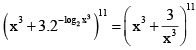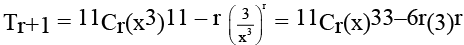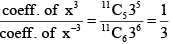JEE Advanced (One or More Correct Option): Mathematical induction & Binomial Theorem | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. Given that the 4th term in the expression of 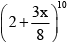 has the maximum numerical value, then x can lie in the interval(s)
has the maximum numerical value, then x can lie in the interval(s)
(a) 
(b) ( -2,- 2)
(c) 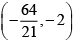
(d) 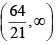
Correct Answer is options (a, c)
Since t4 is numerically the greatest term,
| t3 |<| t4| and | t5 |<| t4 |
⇒
But
⇒
and
⇒
Q.2. For a positive integer n, if the expansion of 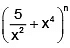 has a term independent of x, then n can be
has a term independent of x, then n can be
(a) 18
(b) 21
(c) 27
(d) 99
Correct Answer is options (a, b, c, d)
Let (r + 1)th term ofbe independent of x, we have
For this term to be independent of x, 6r - 2n = 0 or n = 3r
∴ Each of 18, 21, 27, 99 is divisible by 3.
Q.3. Let 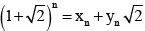 , where xn, yn are integers, then
, where xn, yn are integers, then
(a) 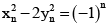
(b) 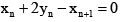
(c) 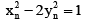
(d) 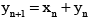
Correct Answer is options (a, b, d)
We have(1)
(2)
From (1) and (2), we get
Next,
=
Thus,and
Q.4. Which of the following is/are true
(a) 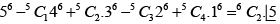
(b) 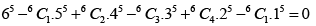
(c) 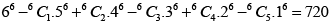
(d) 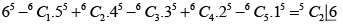
Correct Answer is options (a, b, c)
(A) No. of onto functions from a set containing 6 elements to a set containing 5 elements
=6C2 L5
(B) No .of onto functions from a set containing 5 elements to a set containing 6 elements = 0
(C) No. of onto function from a set containing 6 elements to a set containing 6 elements
= L6 = 720.
Q.5. If (1 + x + x2)n = a0 + a1x + a2x2 + …… + a2nx2n, then
(a) a0 – a2 + a4 – a6 + …… = 0, if n is odd
(b) a1 – a3 + a5 – a7 + …… = 0, if n is even
(c) a0 – a2 + a4 – a6 + …… = 0, if n = 4p, p ∈ I+
(d) a1 – a3 + a5 – a7 + …… = 0, if n = 4p + 1, p ∈ I+
Correct Answer is options (a, b)
Putting. Then, we get
⇒
If n is odd, then Re(in) = 0
⇒ a0 – a2 + a4 – a6 + …… = 0
If n is even, then Im(in) = 0
⇒ a1 – a3 + a5 – a7 + …… = 0
Q.6. The value of the expression 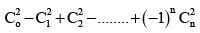 is (Here Ck = nCk)
is (Here Ck = nCk)
(a) 0, if n is odd
(b) (-1)n, if n is odd
(c) (-1)n/2 Cn/2, if n is even
(d) (-1)n-1Cn-1, if n is even
Correct Answer is options (a, c)
When n is odd, taken n = 2m + 1, so that
=
Butetc.
Therefore S = 0
When n is even, we take n = 2m. In this case
= Coefficient of constant term in
= Coefficient of constant term in
= Coefficient of x2m in (1 – x)2m(1 + x)2m = Coefficient of x2m in (1 – x2)2m
=
Q.7. Let an expression E be given by E = (1 + x)n (1 + y)n (1 + z)n then
(a) number of dissimilar terms in E will be (n + 1)3
(b) number of dissimilar terms in E will be n3
(c) coefficient of n r in E is ( nCr )3
(d) Sum of coefficient in E is 23n
Correct Answer is options (a, d)
Each individual expansion will have n +1 terms.
Put x = y = z = 1
Q.8. The cube of any whole number when divided by 9 may yield the reminder
(a) 0
(b) 2
(c) 1
(d) 8
Correct Answer is options (a, c, d)
Any whole number is either 9K, 9K+1, ……, 9K+8 When we cube them reminder will be 0, 1 or 8 only
Q.9. In the expansion of 
(a) there appears a term with the power x2
(b) there does not appear a term with the power x2
(c) there appears a term with the power x-3
(d) the ratio of the co-efficient of x3 to that of x-3 is
Correct Answer is options (b, c, d)
Now 33 – 6r = 2 ⇒ 6r = 31 (not possible)
33 – 6r = –3 ⇒ r = 6
33 – 6r = 3 ⇒ r = 5
∴
Q.10. 1 + x)n − nx − 1 is divisible by (where n∈N)
(a) 2x
(b) x2
(c) 2x3
(d) All of these
Correct Answer is option (b)
(1 + x)n = 1 + nx + ([n (n − 1)] / [2!]) * x2 + ([n (n − 1) (n − 2)] / [3!]) * x3 + . . . . .
(1 + x)n − nx − 1 = x2 [([n (n − 1)] / [2!]) + ([n (n − 1) (n − 3)] / [3!]) * x + . . . . .]
From above it is clear that (1 + x)n − nx − 1 is divisible by x2.
Trick: (1 + x)n − nx − 1, put n = 2 and x = 3;
Then 42 − 2 * 3 − 1 = 9 is not divisible by 6, 54 but divisible by 9, which is given by option (b) i.e., x2 = 9.
|
446 docs|930 tests
|

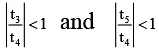

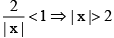
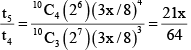
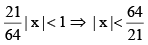
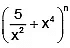 be independent of x, we have
be independent of x, we have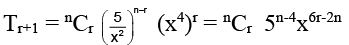
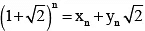 (1)
(1)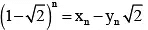 (2)
(2)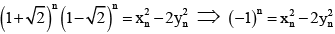
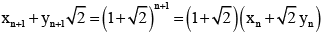

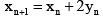 and
and 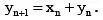
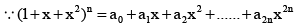
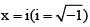 . Then, we get
. Then, we get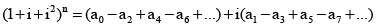
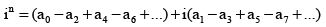
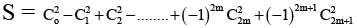
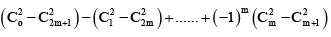
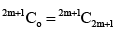
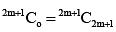 etc.
etc.