JEE Advanced (Single Correct Type): Quadratic Equation & Inequalities | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. The length of a rectangle is three times the breadth. If the minimum perimeter of the rectangle is 160 cm, then
(a) breadth > 20 cm
(b) length < 20 cm
(c) breadth x ≥ 20 cm
(d) length ≤ 20 cm

Correct Answer is option (c)
Let x be the breadth of a rectangle.
So, length = 3x
Given that the minimum perimeter of a rectangle is 160 cm.
Thus, 2 (3x + x) ≥ 160
⇒ 4x ≥ 80
⇒ x ≥ 20

Q.2. If – 3x + 17 < – 13, then
(a) x ∈ (10, ∞)
(b) x ∈ [10, ∞)
(c) x ∈ (– ∞, 10]
(d) x ∈ [– 10, 10)

Correct Answer is option (a)
Given,
-3x + 17 < -13
Subtracting 17 from both sides,
-3x + 17 – 17 < -13 – 17
⇒ -3x < -30
⇒ x > 10 {since the division by negative number inverts the inequality sign}
⇒ x ∈ (10, ∞)

Q.3. The inequality representing the following graph is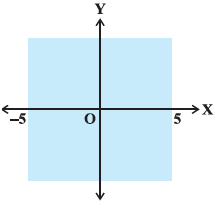
(a) | x | < 5
(b) | x | ≤ 5
(c) | x | > 5
(d) | x | ≥ 5

Correct Answer is option (a)
The given graph shows the shaded region corresponding to x > – 5 and x < 5.
Therefore, by combining the above two inequalities, we get |x| < 5

Q.4. Observe the figure given below.
(a) x ∈ (– ∞, – 2)
(b) x ∈ (– ∞, – 2]
(c) x ∈ (– 2, ∞]
(d) x ∈ [– 2, ∞)

Correct Answer is option (b)
In the given figure, the circle is filled with dark colour at -2 which means -2 is included and the highlighted is towards the left of -2.
So, x ∈ (– ∞, – 2]

Q.5. Given that x, y and b are real numbers and x < y, b < 0, then
(a) x/b < y/b
(b) x/b ≤ y/b
(c) x/b > y/b
(d) x/b ≥ y/b

Correct Answer is option (a)
Given that x, y and b are real numbers and x < y, b < 0.
Consider, x < y
Divide both sides of the inequality by “b”
x/b < y/b {since b < 0}

Q.6. If |x −1| > 5, then
(a) x ∈ (– 4, 6)
(b) x ∈ [– 4, 6]
(c) x ∈ (– ∞, – 4) U (6, ∞)
(d) x ∈ [– ∞, – 4) U [6, ∞)

Correct Answer is option (c)
|x – 1| > 5
x – 1 < – 5 and x – 1 > 5
x < -4 and x > 6
Therefore, x ∈ (-∞, -4) U (6, ∞)

Q.7. If |x – 7|/(x – 7) ≥ 0, then
(a) x ∈ [7, ∞)
(b) x ∈ (7, ∞)
(c) x ∈ (– ∞, 7)
(d) x ∈ (– ∞, 7]

Correct Answer is option (b)
Given,
|x – 7|/(x – 7) ≥ 0
This is possible when x − 7 ≥ 0, and x – 7 ≠ 0.
Here, x ≥ 7 but x ≠ 7
Therefore, x > 7, i.e. x ∈ (7, ∞).

Q.8. If |x + 3| ≥ 10, then
(a) x ∈ (– 13, 7]
(b) x ∈ (– 13, 7]
(c) x ∈ (– ∞, – 13] ∪ [7, ∞)
(d) x ∈ [– ∞, – 13] ∪ [7, ∞)

Correct Answer is option (d)
Given,
|x + 3| ≥ 10
⇒ x + 3 ≤ – 10 or x + 3 ≥ 10
⇒ x ≤ – 13 or x ≥ 7
⇒ x ∈ (– ∞, – 13] ∪ [7, ∞)

Q.9. If 4x + 3 < 6x +7, then x belongs to the interval
(a) (2, ∞)
(b) (-2, ∞)
(c) (-∞, 2)
(d) (-4, ∞)

Correct Answer is option (b)
Given,
4x + 3 < 6x + 7
Subtracting 3 from both sides,
4x + 3 – 3 < 6x + 7 – 3
⇒ 4x < 6x + 4
Subtracting 6x from both sides,
4x – 6x < 6x + 4 – 6x
⇒ – 2x < 4 or
⇒ x > – 2 i.e., all the real numbers greater than –2, are the solutions of the given inequality.
Hence, the solution set is (–2, ∞), i.e. x ∈ (-2, ∞)

Q.10. Solving – 8 ≤ 5x – 3 < 7, we get
(a) –1/2 ≤ x ≤ 2
(b) 1 ≤ x < 2
(c) –1 ≤ x < 2
(d) –1 < x ≤ 2

Correct Answer is option (c)
Given,
– 8 ≤ 5x – 3 and 5x – 3 < 7
Let us solve these two inequalities simultaneously.
– 8 ≤ 5x – 3 and 5x – 3 < 7 can be written as:
– 8 ≤ 5x –3 < 7
Adding 3, we get
– 8 + 3 ≤ 5x – 3 + 3 < 7 + 3
–5 ≤ 5x < 10
Dividing by 5, we get
–1 ≤ x < 2