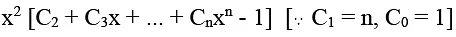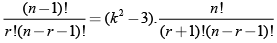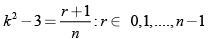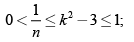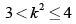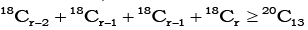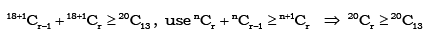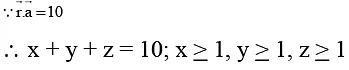JEE Advanced (One or More Correct Option): Permutations & Combinations | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. The number of ways in which 1- candidates A1, A2,….,A10 can be ranked, so that A1 is always above A2 is
(a) 10! / 2
(b) 8! x 10C2
(c) 10P2
(d) 10C2
Correct Answer is Options (a, b)
The number of ways of placing A1 and A2 in ten places so that A1 is always above A2 is 10C2. There are 8! ways of arranging the eight other candidates.
Hence, total number of arrangements
=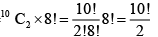
Q.2. If n > 1, then (1 + x)n - nx - 1 is divisible by
(a) x
(b) x2
(c) x3
(d) x4
Correct Answer is Options (a, b)
We have, (1 + x)n - nx - 1 = C0 + C1x + C2x2 ... + Cnxn - nx -1
=
Thus, (1 + x)n - nx - 1 is divisible by x2 and hence by x
Q.3. If 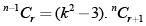 then k may lie in the region
then k may lie in the region
(a) (∞ , 2)
(b) [-2, √3 )
(c) [-√3, 0]
(d) (√3, 2]
Correct Answer is Options (b, d)
Q.4. There are n married couples in a party. Each person shakes hand with every person other than her or his spouse. The total number of handshakes must be
(a) 2nC2 -n
(b) 2nC2 - ( n- 1)
(c) 2n( n - 1)
(d) 2nC2
Correct Answer is Options (a, c)
Total handshakes possible = 2nC2
This will include n handshakes in which a person shakes hand with her or his spouse.
⇒ Required number = 2nC2 – n = 2n(n – 1)
Q.5. The number of selections of four letters taken from the word COLLEGE must be
(a) 22
(b) 18
(c) coefficient of x4 in the expansion of (1 + x + x2)2 (1 + x)3
(d) coefficient of x4 in the expansion of (1 + x + x2)3 (1 + x)2
Correct Answer is Options (b, c)
We have LL; EE; C, O, G Þ Number of selections of four letters = coefficient of x4 in (x0 + x1 + x2)(x0 + x1 + x2)(x0 + x1)(x0 + x1)(x0 + x1)
= coefficient of x4 in (1 + x + x2)2(1 + x)3
⇒ (C) is correct. Since coefficient can be found as 18, (B) is also correct.
Q.6. If 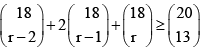 then
then
(a) r = 7
(b) r = 8
(c) r = 9
(d) r = 10
Correct Answer is Options (a, b, c, d)
⇒
So r = 7, 8, 9, 10 are possible answers.
Q.7. Triangles are formed by joining vertices of a octagon then number of triangle
(a) In which exactly one side common with the side of octagon is 32
(b) In which atmost one side common with the side of polygon is 48
(c) At least one side common with the side polygon 50
(d) Total number of triangle 56
Correct Answer is Options (a, b, d)
Total number of triangle = 8C3 = 56
Number of triangle having exactly one side common with the polygon = 8 × 4 = 32
Number of triangle having exactly two side common with the polygon = 8
Number of triangle having no side common with the polygon = 16
Q.8. Total number of ways in which four boys and four girls can be seated around a round table, so that no two girls sit together, is equal to
(a) 4!5!
(b) 3! 4!
(c) 5(4!)2
(d) 4(3!)2
Correct Answer is Options (b, d)
The boys can be arrange in 3! ways around the circle. They form 4 gaps in which girls will occupy difference gaps. So, the girls can now be arrange in 4! ways. So, the total number of ways = 3! 4! = 4 × (3!)2
Q.9. The position vector of a point P is 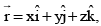 when x, y, z ∈ N and
when x, y, z ∈ N and 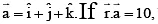
the number of possible position of P is
(a) 36
(b) 72
(c) 66
(d) 9C2
Correct Answer is Options (a, d)
The required number of positions
=10-1C3-1 = 9C2 = 36
Q.10. The number of non-negative integral solution of x1 + x2 + x3 + x4 ≤ n (where n is a positive integer) is
(a) n+3C3
(b) n+4C4
(c) n+5C5
(d) n+4Cn
Correct Answer is Options (b, d)
Let x5 be such that x1 + x2 + x3 + x4 + x5 = n, we now seek the non-negative integral solutions of x1 + x2 + x3 + x4 + x5 = n. The number of required solutions = n+4C4 = n+4Cn
|
446 docs|929 tests
|