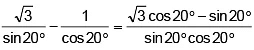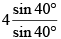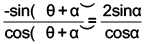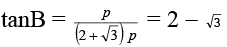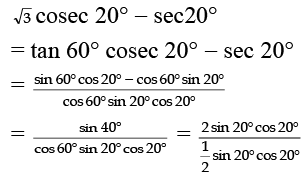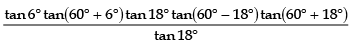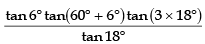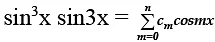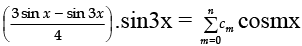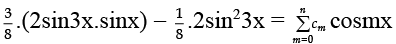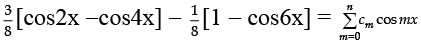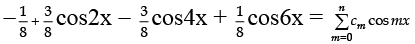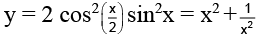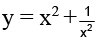Integer Answer Type Questions for JEE: Trigonometric Equations & Functions | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. √3 cosec20° - sec20° =
Ans. 4
Given =
== 4.
=
= 4
Q.2. If sinθ = 3sin(θ + 2α), then the value of tan (θ + α) + 2tanα is:
Ans. 0
Given sin θ = 3sin (q + 2αa)
⇒ sin (θ + α - α) = 3sin (θ + α + α)
⇒ sin (θ + αa) cosα - cos(θ + α) sinα
= 3sin (θ + α) cosαa + 3cos (θ + α) sinα
⇒ -2sin (θ + α) cosα = 4cos (θ + α) sinα
⇒
⇒ tan(θ + a) + 2tanα = 0
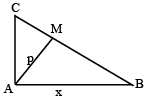
Q.3. In a right angled triangle, the hypotenuse is four times as long as the perpendicular drawn to it from the opposite vertex. One of the acute angles is
Ans. 15
Let AM be perpendicular from A on BC such that AM = p.
Then BC = 4p. Let AB = x, AC = y.
Then x2 + y2 = (4p)2.
In ΔABM, p2 + BM2 = x2
Adding (i) and (ii), 2p2 + (4p -k2) = x2 + y2
⇒ 2p2 + (4p - k2) = (4p)2
⇒ k = 2p - √3 p
∴ BM = BC - CM = 4p - (2p - √3p) = 2p + √3 p
⇒
⇒ B = 15°
Q.4. The value of √3 cosec 20° - sec20° is equal to
Ans. 4
= 4
Q.5. The value of tan 6° tan 42° tan 66° tan 78° is
Ans. 1
We have, tan 6° tan 42° tan 66° tan 78°
= tan 6° tan(60° - 18°) tan(60° + 6°) tan(60° + 18°)
=
=
=
=
= 1
Q.6. Suppose that 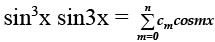 is an identity in x, where c0, c1, c2, …. , cn are constants and cn ≠ 0, find the value of n.
is an identity in x, where c0, c1, c2, …. , cn are constants and cn ≠ 0, find the value of n.
Ans. 6
[Express L.H.S. in multiple of x and compare with R.H.S.].
Given
or,
or,
or,
or,
Comparing, we get n = 6.
[Q Highest multiple of angle on L.H.S. is 6x and on R.H.S. is nx].
Q.7. The number of all possible 5-tuples (a1, a2, a3,, a4, a5 ) such that a1 +a2sinx +a3cosx +a4 sin2x +a5cos2x = 0 holds for all x is
Ans. 1
Since the equation a1 +a2sinx + a3cosx + a4 sin2x + a5 cos2x = 0 holds for all values of x,
a1+ a3 + a5 = 0 ( on putting x = 0)
a1- a3 + a5 = 0 ( on putting x = π)
⇒ a3 = 0 and a1 + a5 =0 . . . . (1)
Putting x = π/2 and 3π/2, we get
a1 + a2 - a5= 0 and a1 - a2 - a5 = 0
⇒ a2 = 0 and a1 – a5 = 0 . . . . (2)
(1) and (2) give
a1 = a2 = a3 = a5 = 0.
The given equation reduces to a4sin2x = 0 . This is true for all values of x , therefore a4 = 0
Hence a1 = a2 = a3 = a4 = a5 = 0.
Thus, the number of 5-tuples is one.
Q.8. The number of solution of 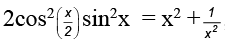 ,0 ≤ x ≤ π/2 is
,0 ≤ x ≤ π/2 is
Ans. 0
We haveis
Let
⇒ y = (1+ cosx) sin2 x and
when y = (1+ cosx) sin2 x = (a number < 2) (a number ≤ 1)
⇒ y < 2 . . . . (1)
and when
⇒ y ≥ 2 . . . . (2)
No value of y can be obtained satisfying (1) and (2), simultaneously
⇒ No real solution of the equation exists.
Q.9. If sinθ = 3sin(θ + 2α), then the value of tan (θ + α) + 2tanα is:
Ans. 0
Given sin θ = 3sin (q + 2αa)
⇒ sin (θ + α - α) = 3sin (θ + α + α)
⇒ sin (θ + αa) cosα - cos(θ + α) sinα
= 3sin (θ + α) cosαa + 3cos (θ + α) sinα
⇒ -2sin (θ + α) cosα = 4cos (θ + α) sinα
⇒
⇒ tan(θ + a) + 2tanα = 0
Q.10. The value of the expression 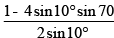 is
is
Ans. 1
Given expression is
=
=
= 1
|
446 docs|929 tests
|