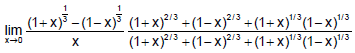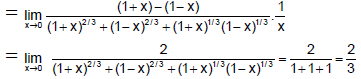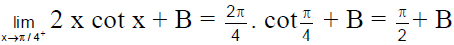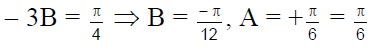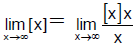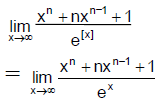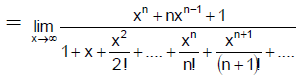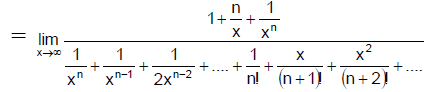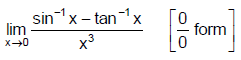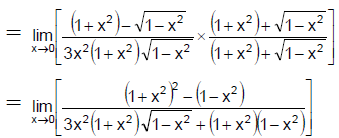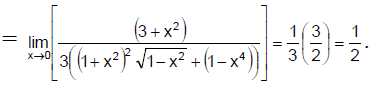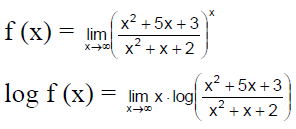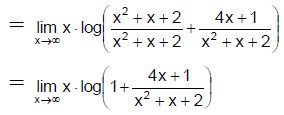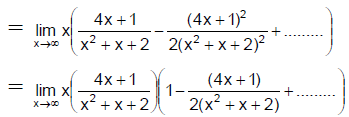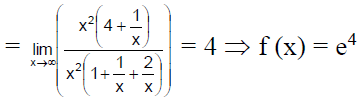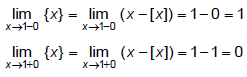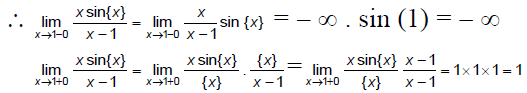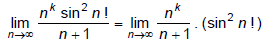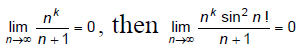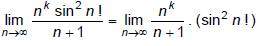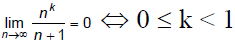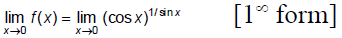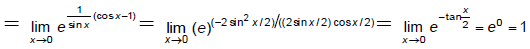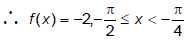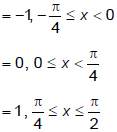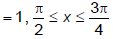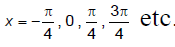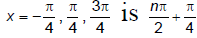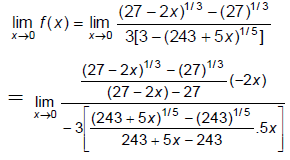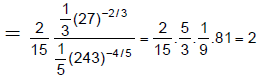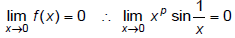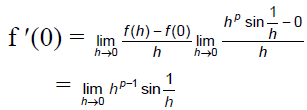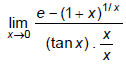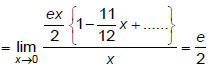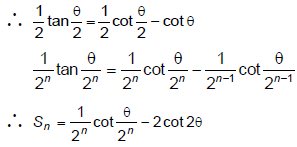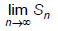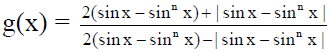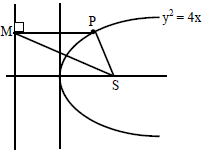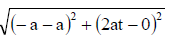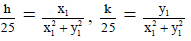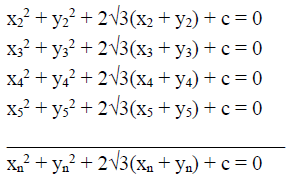JEE Advanced (Single Correct Type): Limits, Continuity & Differentiability | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. The value of 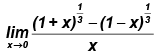 is:
(a) 2/3
(b) 1/3
(c) 1
(d) 5/3

Correct Answer is option (a) 


Hence, (a) is the correct answer.

Q.2. The values of A and B so that function f (x) defined by

become continuous, respectively are
(a) -π/12, π/6
(b) π/6, -π/12
(c) P/12, π/6
(d) π/6, P/12

Correct Answer is option (b) 

L.H. limit at x < (π/4)

R.H. limit =
 ...(1)
L.H. limit at x < (π/2)

RH limit = x  + A cos 2x - B sin x = A cos π - B sin(π/2)
= - A - B
- A - B = B ⇒ a = - 2B … (2)

Hence, (b) is the correct answer.

Q.3. The value of  is:  
(a) 1
(b) 0
(c) n
(d) n(n –1)

Correct Answer is option (b) 






Hence, (b) is the correct answer.

Q.4. 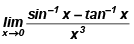 is equal to
(a) 2
(b) 1
(c) –1
(d) 1/2

Correct Answer is option (d) 

 (L’ Hospital rule)


Hence, (d) is the correct answer.

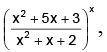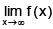Q.5. If f (x) = then  is
(a) e⁴ 
(b) e³ 
(c) e² 
(d) 2⁴

Correct Answer is option (a) 




Hence, (a) is the correct answer.

Q.6. 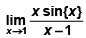, where {x} denotes the fractional part of x, is
(a)-1
(b) 0
(c)1
(d) does not exist

Correct Answer is option (d) 


Since, L.H. limit ≠ R.H. limit
∴ limit does not exist.
Hence, (d) is the correct answer.

Q.7. If 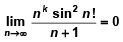 for
(a) all k
(b) 0 ≤ k < 1
(c) k = 1
(d) for k > 1

Correct Answer is option (b) 

 does not exist but if

But
Hence, (b) is the correct answer.

Q.8. If 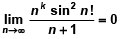 for
(a) all k
(b) 0 ≤ k < 1
(c) k = 1
(d) for k > 1

Correct Answer is option (b) 

 does not exist but if
 then  
But,
Hence, (b) is the correct answer.

Q.9. If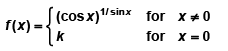
The value of k, so that f is continuous at x = 0 is
(a) 0
(b) 1
(c) 1/2
(d) none of these 

Correct Answer is option (b) 
Given, f(0) = k


For f(x) to be continuous at x = 0, k = 1.
Hence, (b) is the correct answer.

Q.10. If f(x) = [√2 sin x ] , where [x] denotes the greatest integer function, then
(a) f(x) is continuous at x = 0
(b) maximum value of f(x) is 1 in interval [-2π, 2π]
(c) f(x) is discontinuous at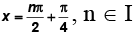
(d) f(x) is differentiable at x = nπ, n ∈ I

Correct Answer is option (b) 
f (x) = [√2 sin x]



 clearly f(x) is discontinuous at

General value corresponding to
maximum value of f(x) in [-2π, 2π] is 1 at x = π/2.
f(x) is discontinuous and non-differentiable at x = 0 therefore choice (d) is not correct.
Hence, (b) is the correct answer.

Q.11. The value of f(0), so that the function f(x) =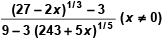 is continuous is
(a) 2/3
(b) 6
(c) 2
(d) 4

Correct Answer is option (c) 


Hence, (c) is the correct answer.

Q.12. Let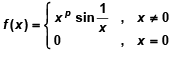
Then f(x) is continuous but not differentiable at x = 0 if
(A) p < 0
(B) p = 0
(C) 0 < p ≤ 1
(D) p ≥ 1

Correct Answer is option (c) 
f(0) = 0
For f(x) to be continuous at x = 0

This is possible only when p > 0 …(i)

f'(0) = will exist only when p > 1
∴ f(x) will not be differentiable if p ≤ 1 …(ii)
From (i) and (ii), for f(x) to be not differentiable but continuous at x = 0, possible values of p are given by 0 < p ≤ 1.
Hence, (c) is the correct answer.

Q.13.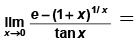  
(a) e
(b) e/2
(c) e² 
(d) none of these

Correct Answer is option (b)

 [using expansion]

Hence, (b) is correct answer.

Q.14.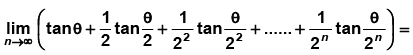
(a) 1/θ
(b) (1/θ) - 2 cot2θ
(c) 2cot 2θ
(d) none of these 

Correct Answer is option (b) 
tanθ = cotθ  - 2 cot 2θ

∴ Required limit =

= (1/θ) - 2cot2θ
Hence, (b) is correct answer.

Q.15. If g(x) = 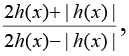 where h(x) = sinx - sinⁿx, n ∈ R⁺, the set of positive real numbers, and f(x) =  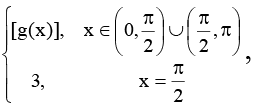where, [x] denotes the greatest integer function, then
(a) f(x) is continuous and differentiable at x = (π/2), when  0 < n < 1
(b) f(x) is continuous and differentiable at x =(π/2), when n > 1
(c) f(x) is continuous but not differentiable at x =(π/2), when 0 < n < 1
(d) f(x) is continuous but not differentiable at x = π/2, when n > 1

Correct Answer is option (b) 

for 0 < n < 1, sinx < sinⁿx, g(x) = (1/3) & for n > 1, sinx > sinⁿx, g(x) = 3
∴ for n > 1, f(x) = 3, x ∈ (0, π)
∴ f(x) is continuous and differentiable at x = π/2 & for 0 < n < 1

∴ f(x) is not continuous at x = π/2.
Hence, f(x) is also not differentiable at x = π/2.

Q.16. If f (x) = x + 2 (1 ≤ x ≤ 2) and g(x) = x (2 ≤ x ≤ 3). Then f(g(x)) is
(a) f(g(x)) = x + 2,  (1 ≤ x ≤ 2)
(b) f(g(x)) = 4, x = 2
(c) f(g(x)) = x + 2, (2 ≤ x ≤ 3)
(d) f(g(x)) = 2, x = 2

Correct Answer is option (b) 
Equation of the required circle may be given as x² -y² + 2(cxy - 2x + 1 + λ(y² - 4(c + 1)x)

since coefficient of xy = 0
⇒ c = 0
coefficient of x² = coefficient of y²
⇒ 1 = -1 + λ ⇒ λ = 2
By putting the values of λ and c we get the equation of the required circle as
x² + y² -10x + 1 = 0 ⇒ center of the circle is (5, 0).

Q.17.  is
(a) 0
(b) 1
(c) 1/2
(d) does not exist

Correct Answer is option (a) 

Let the coordinate of P is (at², 2at)
Coordinate of M will be (-a, 2at), the coordinate of S(focus) will be (a, 0)
Since the triangle PMS is equilateral triangle
⇒ PM = MS = PS
⇒ at² + a =
⇒ t = ±3
⇒ (at², 2at) ≡ (3, 2√3) or (3, -2√3)

Q.18. 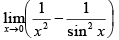 is
(a) 1
(b) 1/3
(c) -1/3
(d) does not exist

Correct Answer is option (a) 
Centre of C₃ will lie on the radical axis of C₁ and C₂ which is 10x + 6y + 26 = 0.
Let center of C₃ is (h, k).
Equation of chord of contact through (h, k) to the C₁ may be given as hx + ky = 25 ...(I)
Let the mid point of the chord is (x₁, y₁) the equation of the chord with the help of mid point may be given as xx₁ + yy₁ = x₁² + y₁² ...(II)
Since, (I) and (II) represents same straight lines
⇒
Since, (h, k) lie on the radical axis 10x + 6y + 26 = 0
⇒  ⇒ the locus of (x₁, y₁) is 5x + 3y + (13/25)(x² + y²) = 0

Q.19.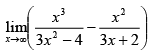
(a) does not exist
(b) 1/3
(c) 0
(d) 2/9

Correct Answer is option (a) 
In the given equation of parabola the focus is (1, 1) and equation of directrix is
x + y + 2 = 0
⇒ axis of parabola is y = x.
Vertex of the parabola C is (0, 0). Let a is the distance between vertex and focus = √2 the distance of the point on the axis from which three normals may be drawn will be minimum 2a from the vertex which is equal to 2√2 coordinate the point nearest to the vertex from which three normals may be drawn can be given as (2, 2).
⇒ h ≥ 2.

Q.20. If f (x) = 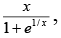 x ≠ 0, f(0) = 0 then
(a) f (x) is continuous at x = 0 and f'(x) = 1
(b) f (x) is discontinuous at x = 0
(c) f(x) is continuous at x = 0 and f'(x) does not exist
(d) f (x) is continuous at x = 0 and f'(x) = 0

Correct Answer is option (b) 
Equation of the circle with center (√3, √3) may be given as x² + y² + 2√3(x + y) + c = 0
Let (x₁, y₁), (x₂, y₂), (x₃, y₃) … (x₄, y₄) are the rational points satisfying the equation of circles
⇒ The following relations holds good x₁² + y₁² + 2√3(x₁ +y₁) + c = 0

All the above relations may holds only if
x₁ + y₁ = 0, x₂ + y₂ = 0…..x_n + y_n = 0
⇒ If any rational point (x_r, y_r) lie on the circle it should also satisfy the straight line x + y = 0. Since there may be at the most two points of intersection between a circle and a straight line.
⇒ There are at the most two rational points lying in the circle.