JEE Advanced (Single Correct Type): Differential Equations | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. hat is the order of differential equation y’’ + 5y’ + 6 = 0?
(a) 0
(b) 1
(c) 2
(d) 3
Correct Answer is option (c)
Given, differential equation y’’ + 5y’ + 6 = 0. The highest order derivative present in the differential equation is y’’. Hence, the order is 2.
Q.2. The differential equation representing the family of curves y2 = 2c (x + √c) , where c is a positive parameter, is of
(a) order 1
(b) order 2
(c) degree 2
(d) degree 1
Correct Answer is option (a)
We have, y2 = 2c (x + √c) ...(i)
⇒ 2y y1 = 2c ⇒ yy1 = c ...(ii)
Eliminating c from (i) and (ii), we get )y2 = 2yy1(x +
⇒ (y - xy1)2 = y y31
Clearly, it is a differential equation of order one and degree 3.Hence, (A) is the correct answer.
Q.3. What is the degree of differential equation (y’’’)2 + (y’’)3 + (y’)4 + y5 = 0?
(a) 2
(b) 3
(c) 4
(d) 5
Correct Answer is option (a)
The degree is the power raised to the highest order derivative. Therefore, in the given differential equation, (y’’’)2 + (y’’)3 + (y’)4 + y5 = 0, the degree will be power raised to y’’’.
So, the answer is 2.
Q.4. For any differentiable function y = f(x), the value of 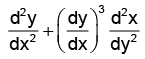 is
is
(a) always zero
(b) always non-zero
(c) equal to 2y2
(d) equal to x2
Correct Answer is option (a)
for a differential coefficient
Hence, (a) is the correct answer.
Q.5. Find the order of differential equations:
(a) 2
(b) 1
(c) 0
(d) Undefined
Correct Answer is option (a)
Given, the differential equation is:
Or we can write:
2x2 y’’ – 3y’ + y = 0
Order is the highest derivative in the differential equation. Therefore, the order is 2.
Q.6. Find the degree of the differential equation.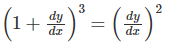
(a) 0
(b) 1
(c) 2
(d) 3
Correct Answer is option (d)
Given, the differential equation is:
We can expand it and get:
The exponent of highest derivative is the degree. Therefore, the degree is 3.
Q.7. The number of arbitrary constants in the particular solution of a differential equation of third order is:
(a) 3
(b) 2
(c) 1
(d) 0
Correct Answer is option (d)
The solution free from arbitrary constants i.e., the solution obtained from the general solution by giving particular values to the arbitrary constants is called a particular solution of the differential equation.
Q.8. Which of the following is a second-order differential equation?
(a) (y’)² + x = y²
(b) y’y” + y = sin x
(c) y”’ + (y”)² + y = 0
(d) y’ = y²
Correct Answer is option (b)
The order of y’y” + y = sin x is 2. Thus, it is a second-order differential equation.
Q.9. The function f(θ) = 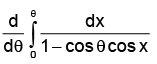 satisfies the differential equation
satisfies the differential equation
(a) 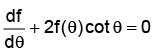
(b) 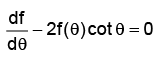
(c) 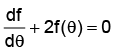
(d) 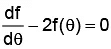
Correct Answer is option (b)
We have f(θ) =
Therefore df(θ) = -2cosec2θ cotθ
Hence, (a) is the correct answer.
Q.10. If f(x), g(x) be twice differentiable function on [0, 2] satisfying f "(x) = g ''(x), f '(1) = 4 and g'(1) = 6, f(2) = 3, g(2) = 9, then f(x) - g(x) at x = 4 equals
(a) 0
(b) -10
(c) 8
(d) 2
Correct Answer is option (b)
We have f ''(x) = g ''(x)
Integrating, we get f '(x) = g '(x)+ c
Putting x = 1, we get f '(1) = g '(1) + c ⇒ c = -2
⇒ f'(x) = g'(x) - 2 ⇒ f(x) = g(x) - 2x + C1 ⇒ f(2) = g(2) - 4 + C1 ⇒ C1 = -2
Thus we have f(x) = g(x) - 2x - 2
⇒ f(4) - g(4) = -10
Hence, (B) is the correct answer.
Q.11. The degree and order of the differential equation of all parabolas whose axis is x-axis are
(a) 2, 1
(b) 1, 2
(c) 3, 2
(d) none of these
Correct Answer is option (b)
Equation of required parabola is of the form y2 = 4a(x –h)
Differentiating, we have
Required differential equation
Degree of the equation is 1 and order is 2.
Hence, (B) is the correct answer.
Q.12. Solution of 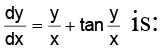
(a) sin (y/x) = kx
(b) cos y/x = kx
(c) tan y/x = kx
(d) none of these
Correct Answer is option (b)
put y = vx ⇒ v += v + tan v
cot v dv = dx/v
Integrating, we get ln sin v = ln x + ln k ⇒ sin y/x = kx
Hence, (A) is the correct answer.
Q.13. If y = e–x (A cosx + B sin x), then y satisfies
(a) 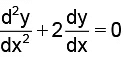
(b) 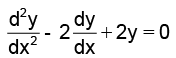
(c) 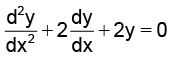
(d) 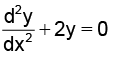
Correct Answer is option (c)
y = e–x (A cos x + B sin x) ....(1)
⇒ dy/dx = e-x (–A sin x + B cos x) – e–x (A cos x + B sin x)
⇒ dy/dx = e-x (–A sin x + B cos x) – y .....(2)
⇒ d2y/dx2 = e-x (–A cos x – B sin x) – e–x (–A sin x + B cos x)
Using (1) and (2), we get
Hence, (C) is the correct answer.
Q.14. If 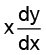 = y (logy – logx + 1) then the solution of the equation is:
= y (logy – logx + 1) then the solution of the equation is:
(a) 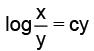
(b) 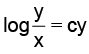
(c) 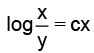
(d) 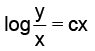
Correct Answer is option (d)
Put y = vx ⇒
⇒ log(log v) = logx + logc = logcx
⇒ log v = cx ⇒= cx
Hence, (D) is the correct answer.
Q.15. The differential equation of all ellipses centerd at the origin and major and minor axes along coordinate axes is
(a) y2 + xy12 - yy1 = 0
(b) xyy2 + xy12 -yy1 = 0
(c) yy2 + xy12 - xy1 = 0
(d) none of these
Correct Answer is option (b)
The given family of curves is...(1)
where a and b are parameters...(2)
Differentiating again, we have..(iii)
Multiplying (iii) with x and then subtracting from (ii), we have
(1/b2) (yy1 - xy12 - xyy2) = 0 ⇒ xyy2 + xy12 - yy1 = 0
|
446 docs|930 tests
|

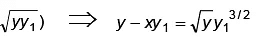 ⇒ (y - xy1)2 = y y31
⇒ (y - xy1)2 = y y31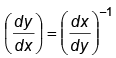 for a differential coefficient
for a differential coefficient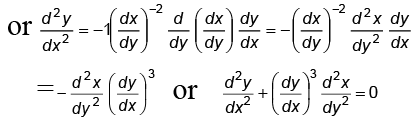
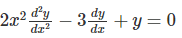
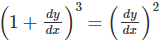
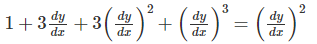
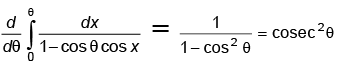
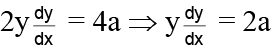
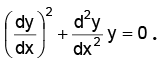
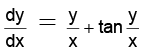
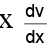 = v + tan v
= v + tan v 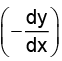
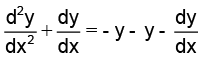
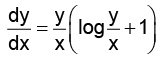
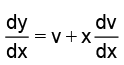
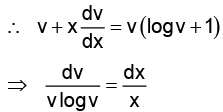
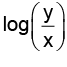 = cx
= cx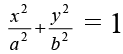 ...(1)
...(1)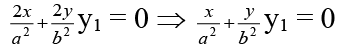 ...(2)
...(2)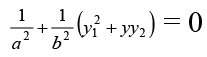 ..(iii)
..(iii)




















