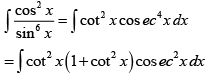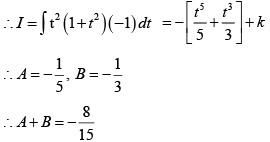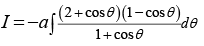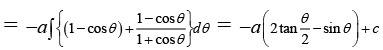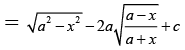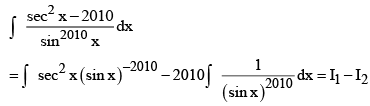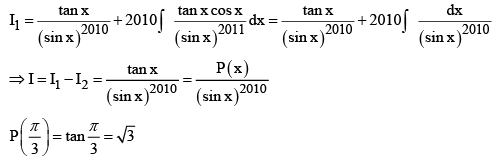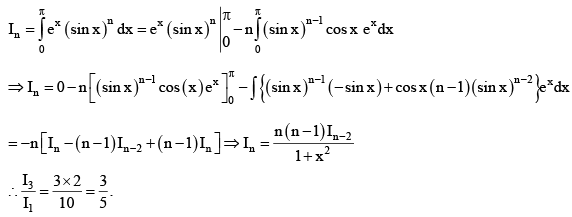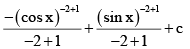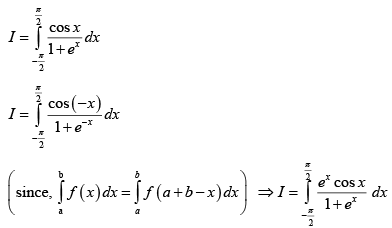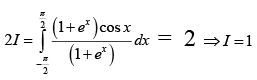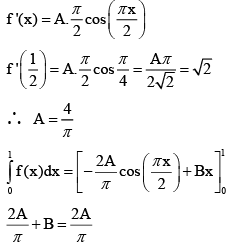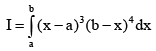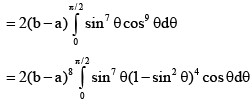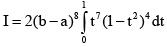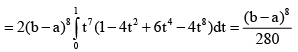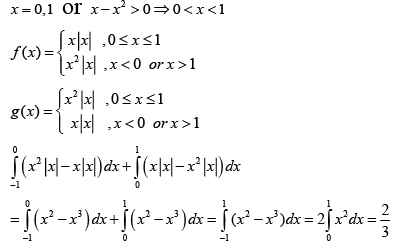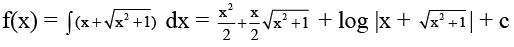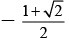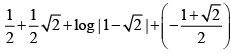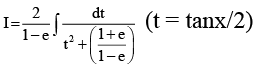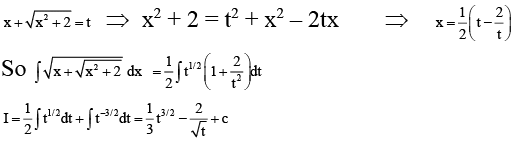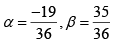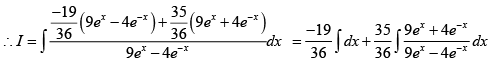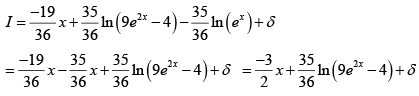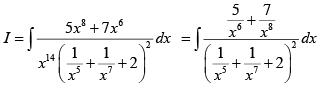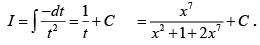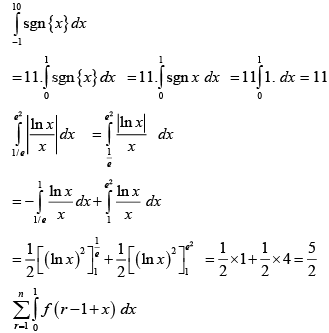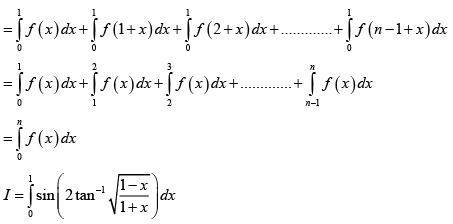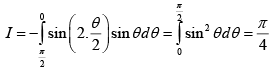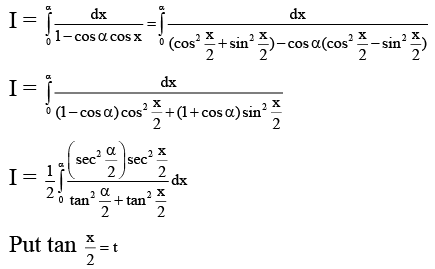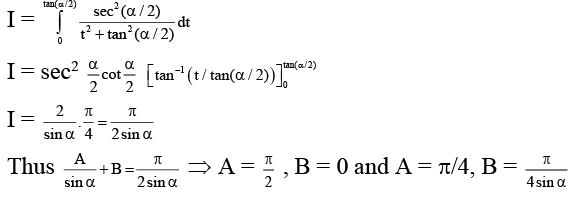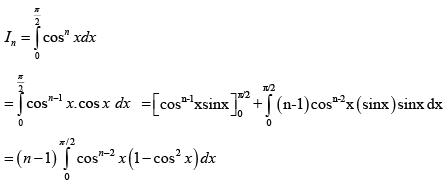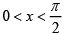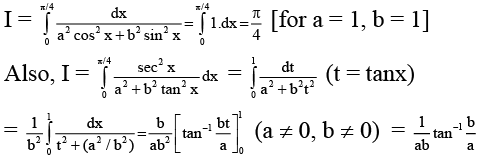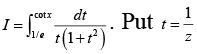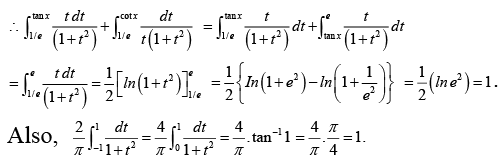JEE Advanced (One or More Correct Option): Applications of Derivatives | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. If 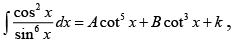then A + B equals
(a)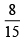
(b)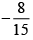
(c)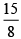
(d)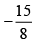

Correct Answer is option (a)

Put t = cotx

Q.2.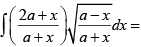
(a)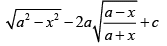
(b)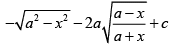
(c)
(d)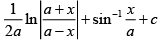

Correct Answer is option (a)
Put  Then 0 < θ < π
and

Q.3. If 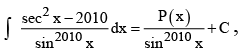then value of 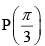is
(a) 0
(b)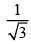
(c) √3
(d) None of these

Correct Answer is option (c)

Applying by parts on I₁, we get

Q.4. If 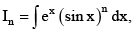then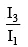is equal to
(a) 3/5
(b) 1/5
(c) 1
(d) 2/5

Correct Answer is option (a)

Q.5. 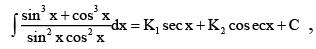then which of the following is correct?
(a) K₁ = K₂ = 1
(B) K₁ = -K₂ = 1 
(C) K₁ = K₂ = -1
(D) K₂ = 1 and K₁ = -1

Correct Answer is option (b)

Putting cosx = t  and sin x = t respectively.
⇒
⇒ sec x – cosec x + c    Þ K₁ = 1,  K₂ = -1

Q.6. The value of 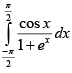is
(a) 0
(b) 1
(c) 2
(d) π

Correct Answer is option (b)

On adding we get

Q.7. Let 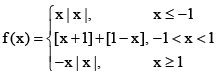where [.] denotes the greatest integer function, then the value of 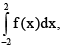is equal to
(a)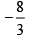
(b)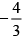
(c) 8/3
(d) 4/3

Correct Answer is option (a)

f(x) = -x², x < - 1
1, -1 < x < 0
2, x = 0
1, 0 < x < 1
-x², x > 1
f(x) is an even function.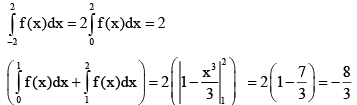
 

Q.8. If 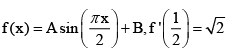and 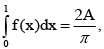then the constants A and B are respectively
(a)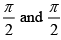  
(b)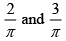
(c)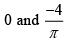
(d)

Correct Answer is option (d)

∴ B = 0

Q.9. The value ofThen (m, n) is

(a) (6, 260)
(b) (8, 280)

(c) (4, 240)
(d) none of these

Correct Answer is option (b)

∴
(a cos²θ + b sin²θ - (A)³ (b – a cos²θ - b sin²θ)⁴
sinθ cos θ dθ

Let sin θ= t  Þ cos θ dθ = dt
⇒

Q.10. Let f (x) be maximum and g (x) be minimum of {x | x |, x² | x |} then
(a) 1/12
(b) 1/3
(c) 2/3
(d) 7/12

Correct Answer is option (c)

Q.11. If f '(x) = 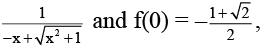then f(1) is equal to
(a) - log ( √2 - 1)  
(b) 1
(c) 1 + √2
(d) log (1 + √2)

Correct Answer is option (A, D)

Putting x = 0, f(0) = c so c =
and f(1) =
= log (1 + √2) = - log (√2 - 1)

Q.12. The value of 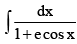must be same as
(a) 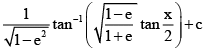(e lies between 0 and 1)
(b) 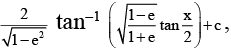(e lies between 0 and 1) 
(c) 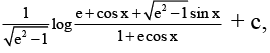 (e is greater than 1) 
(d) 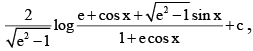(e is greater than 1) 

Correct Answer is option (B, C)

if 0 < e < 1, So,  (B) is correct
If e > 1, So, (C) is correct. 

Q.13. If 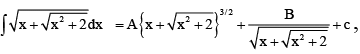then
(a) A = 1/3
(b) B = -2
(c) A = 2/3
(d) B = -1

Correct Answer is option (A,B)

Q.14. If 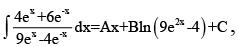then
(a) A = 3/2
(b) B = 35/36
(c) C is indefinite
(d)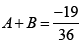

Correct Answer is option (B, C, D)

We write 4e^x + 6e^-x = α(9e^x -4e^-x) + β(9e^x + 4e^-x)
So 9α + 9β = 4 -4α + 4β  = 6


where δ is integration constant

On comparing with I = Ax + B ln (9e^2x - 4) + C
is indefinite

Q.15. If 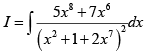then I is equal to
(a)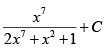
(b)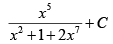
(c)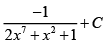
(d)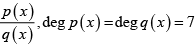

Correct Answer is option (A, D)

We can write

Put so that

Q.16. Which of the following options is/are correct? 
(a) 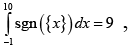where {x} is fractional part of x .
(b)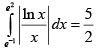
(c)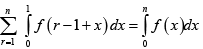
(d)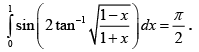

Correct Answer is option (B, C)

put x = cosθ ⇒ dx = - sinθ dθ

Q.17. If 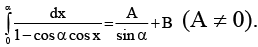Then possible values of A and B are
(a) A = π/2, B = 0
(b) A = π/4, B = p/4sinα
(c) A = π/6, B = p/sinα
(d) A = π, B = p/sinα

Correct Answer is option (A, B)

Satisfy the last equation.

Q.18. Let 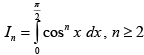is natural number,  then
(a) 1_n-2 > I_n
(b) n (l_n-2 - I_n) = I_n-2
(c)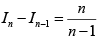
(d)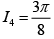

Correct Answer is option (A, B)

I_n =(n -1) I_n-2, -(n -1) I_n

n_In = (n -1) I _n-2

n (l_n-2 - I_n ) = I_n-2

Clearly I_n-2 > I_n
Also for
0 < cos x< 1

So, cosⁿ x < cos^n-1x
⇒ I_n < I_{n - 1}

Q.19. The value of the integral I = 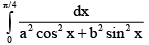is
(a) 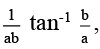(a > 0, b > 0)
(b) 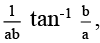(a < 0, b < 0) 
(c) 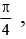(a = 1, b = 1)
(d)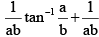

Correct Answer is option (A, B, C)

Q.20. The value of 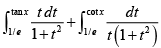is
(a)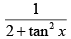
(b) 1
(c) π/4
(d)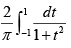

Correct Answer is option ( B, D)

Let