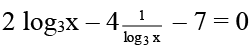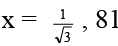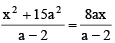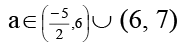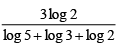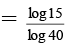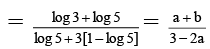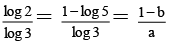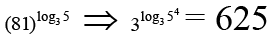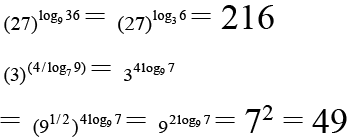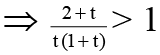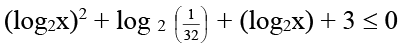JEE Advanced (One or More Correct Option): Logarithms | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. If a ≠ 0 then the inequation |x – a| + |x + a| < b
(a) Has no solution if b ≤ 2 |a|
(b) Has a solution set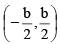 if b > 2 |a|
if b > 2 |a|
(c) Has a solution set 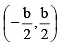 if b < 2 |a|
if b < 2 |a|
(d) Has no solution if b > 2|a|
Correct Answer is option (a and b)
If a > 0
2x < b if x > a
2a < b if – a < x < a
– 2x < b if x < – a
If a < 0 Þ 2x < - a if x > - a
– 2a < b if a < x < – a
– 2x < b if x < a
Hence b > 2|a| if – a < x < a
⇒ b > 2|a| if⇒ B is true and for
b ≤ 2|a| hence no solution
So A, B are true.
Q.2. If logax = b for permissible values of a & x then which is/are correct
(a) If a & b are true irrational numbers then x can be rational
(b) If a is rational & b is irrational then x can be rational
(c) If a is irrational & b is rational then x can be rational
(d) If a is rational & b is rational then x can be rational
Correct Answer is option (a, b, c and b)
(A) ∴ x = ab
If a = (√2)√2 irrational
b = √2 irrational
then ab = ((√2)√2)√2 = 2 which is rational
(B) If a = 2 ∈Q
b = log2 3 ∉Q
then ab = 3 ∈ Q
C & D can be easily checked
Q.3. The x-values satisfying the equation 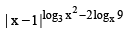 = (x – 1)7 is/are
= (x – 1)7 is/are
(a) 1/√3
(b) 1
(c) 2
(d) 81
Correct Answer is option (c and d)
L.H.S. + ve ⇒ x > 1
So log3 x2 – 2logx9 = 7 or x –1=1 ⇒ x = 2
2(log3x)2 – 7 log3x – 4 = 0 ⇒ log3x = -1/2, 4
x = 3–1/2, 34
1/√3 neglect because x > 1
So x = 2, 81
Q.4. If x = 9 is solution of λn (x2 +15a2) -λn (a - 2) = λn (8ax/a-2) then
(a) a = 3/5
(b) a = 3
(c) x = 15
(d) x = 2
Correct Answer is option (b and c)
Θ a > 2
Also 8ax/a-2 > 0
∴ x > 0 as a > 2
Now
⇒ x2 – 8ax + 15a2 = 0
⇒ x = 3a, 5a
∴ x = 9 (given)
⇒ x = 3, 9/5
But a > 2
∴ a = 3
at a = 3 ⇒ x = 9, 15
Q.5. If y = log7–a (2x2 + 2x + a + 3) is defined 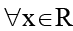 then possible integer value of a is/are
then possible integer value of a is/are
(a) 4
(b) – 3
(c) – 2
(d) 5
Correct Answer is option (a, c and d)
Θ 2x2 + 2x + a + 3 > 0
∴ D < 0
⇒ a > -5/2 ... (1)
Also 7 – a > 0
⇒ a < 7 ……(ii)
& 7 – a ≠ 1
a ≠ 6 ……(iii)
from (i) (ii) & (iii)
Q.6. In which of the following m > n (m, n ∈ R)
(a) m = (log25)2 & n = log 220
(b) m = log102 & n = log10 3√10
(c) m = log105. log1020 + (log102)2 & n = 1
(d) m = log1/2 (1/3) & n = log1/3 (1/2)
Correct Answer is option (a and d)
(A) m – n = (log25)2 – (log25 + 2) = (log25 – 2) (log25 + 1) > 0
∴ m > n
(B) m = 0·3010, n = 1/3 ∴ m < n
(C) m =(1 – log102)(1 + log102) = 1– log2102 < 1
(D) m = log23, n = log32 ∴ m > n
Q.7. If log105 = a and log103 = b then
(b) log30 8 = 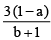
(b) log40 15 = 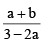
(c) log24332 = 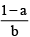
(d) All above
Correct Answer is option (a, b, c and d)
(A) log30 8 =
But log 2 = 1 – log 5 = 3 (1 – a) /(b + 1)
Hence choice [A] is true.
(B) log4015
Hence choice [B] is true.
(C) log243 32 =
Hence choice [C] is true.
Thus correct choice are (A),(B), (C) and (D)
Q.8. Which among the following are true?
(a) 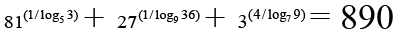
(b) 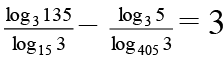
(c) 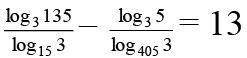
(d) All above
Correct Answer is option (a and b)
(A)
So sum = 890
⇒ Choice [A] is true.
(B) [log3(33 × 5)]. [log3 (3×5)] – log35 [log3(34 × 5)] = 3
⇒ choice [B] is true.
If (B) is true (C) can’t be true.
Q.9. The inequation (logx2) (log2x2) (log24x) >1
(a) Has a meaning for all x
(b) Has a meaning if x > 2
(c) is satisfied in 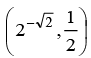
(d) is satisfied in (1, 2√2)
Correct Answer is option (b, c and d)
logx 2 is defined x > 0 and x ≠ 3
log2x 2 is defined x > 0 and x ≠ 1/2
log24x is defined x > 0
⇒ domain of function
(A) (logx2) (log4x2) (log24x) is x > 0
and x ≠ 1 and x ≠ 1/2
So choice [A] is ruled out.
(B) Since x > 2 is sub-set of domain f g(x).
So choice (B) is true.
Given expressions1 put log2 x = t
If numerator and denominator > 0
⇒ t2 + t –t –2 < 0
⇒ – √2 < t < √2
⇒ 2–√2 < x < 2√2
Choices (C) and (D) are satisfied
Q.10. Integers satisfying the inequality log22 x + log2 0.03125x + 3 ≤ 0 is/are –
(a) – 1
(b) 0
(c) 2
(d) 1
Correct Answer is option (c and d)
⇒ (log2x)2 + (log2x) - 2 ≤ 0
⇒ (log2x + 2) (log2x - 1) ≤ 0
⇒ - 2 ≤ log2x ≤ 1
⇒ 1/4 ≤ x ≤ 2
So integers are x = 1, 2
|
446 docs|930 tests
|