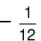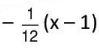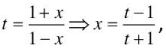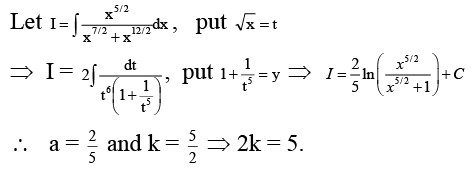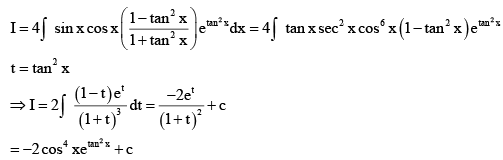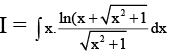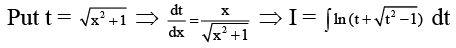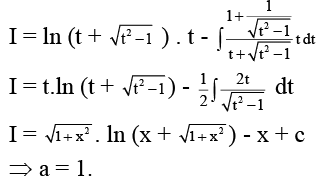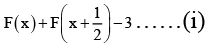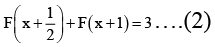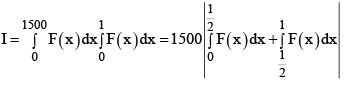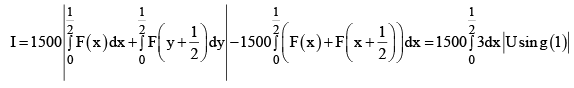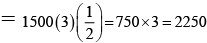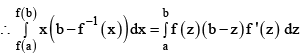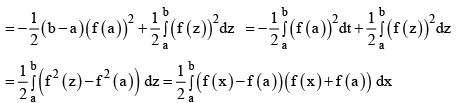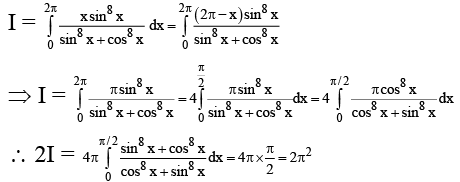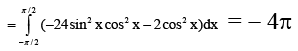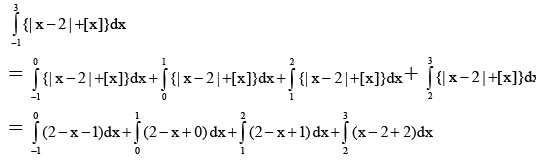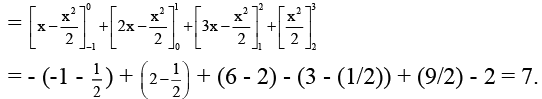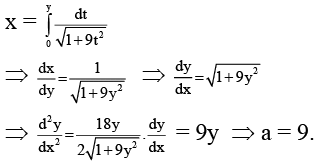Integer Answer Type Questions for JEE: Applications of Derivatives | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. If the normal to the curve x = t - 1, y = 3t² - 6 at the point (1, 6) make intercepts a and b on x and y-axes respectively, then the value of a + 12b is___________

Ans. 146
Given point is corresponding to t = 2 and = 6t ⇒ slope of normal at t = 2 is
∴ equation of normal is y-6 =
⇒ a = 73, b =a + 12b = 146

Q.2. Equation of the normal to the curve y = ( l + x )^y + s in ^-1 ( sin ² x ) at x = 0 is x + y = k, then k is

Ans. 1
{nx + n} has period = 1
tan πx/2 has period = 2

∴ net period = 2.3.

Q.3. The curve y = ax³ +bx²+cx +5, touches the x-axis at P(-2, 0) and cuts the y-axis at a point Q, where its gradient is 3, then find the value of 4b -2a + c.

Ans. 1
Let y = f(x), f ' ( - 2 ) = 0 , f ( - 2 ) = 0
f ’(0 )= 3, f' (x ) = 3ax² +2bx +c
Solving a = and c = 3 ⇒ 4b - 2a + C = 1

Q.4. if 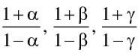are roots of the polynomial equation p(x)=0, where α, β, γ are roots of the equation 3x³ - 2 a + 5 = 0. Then number of negative real roots for the equation p (x) = 0 is

Ans. 1
Put
which reduces th e given eq uation to 6t³ + 4t² + 26t+ 4 = 0
⇒ P(x) = 6x³ + 4x² + 26x + 4
Since P'(x)>0 and p(0)>0
Therefore P(x) = 0 has only one negative real root.

Q.5. Tangents are drawn from P(6, 8) to the circle x² + y² = r². Then the radius of the circle such that the area of the triangle formed by tangents and chord of contact is maximum is________.

Ans. 5

Q.6. If 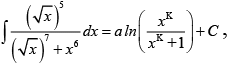then the value of  2k is 

Ans. 5

Q.7. If 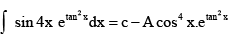then A=___

Ans. 2

Q.8. If f'(x) = 3x² sin 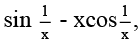x ≠ 0, f(0) = 0 then the value of 

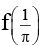is

Ans. 0

 
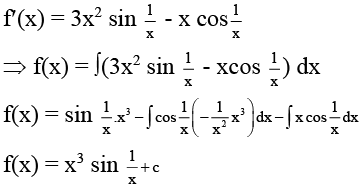
f(0) = 0 + c = 0 ⇒ c = 0
sinπ + 0 = 0.

Q.9.  If 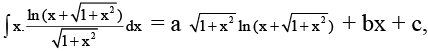then the value of 'a' is 

Ans. 1

Q.10. Let F (x) be a non-negative continuous function defined on R such tha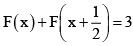and  the value of 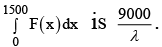Then the numerical value of λ is

Ans. 4

We have
Replace x by in (I), we get
⇒ F(x) is periodic function.
Now consider

Put integral, we get

Hence I

Q.11. If : R → R is a monotonic, differentiable real valued function, a, b are two real numbers and 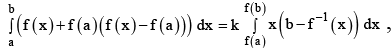then find the value of k

Ans. 2

If : R → R is a monotonic    

Since f(x) is monotonic, therefore, f^-1 (x) exists.
Let f^-1 (x) = z, then x = f(z)
x = f (a) ⇒ z = f ^-1 (f (a)) = a, x = f (b)
⇒ z = f ^-1 (f (b)) = b and dx = f' (z) dz

{integrating by parts}

∴ k = 2

Q.12. If 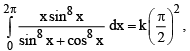then the value of k is

Ans. 4

∴ I = π². Hence K = 4.

Q.13. If 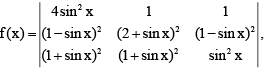then evaluate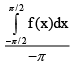 

Ans. 4

Applying C1 → C1 – C3 and C2 → C2 – C3, we get
 
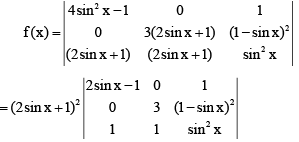
= -16sin³x cos²x - 24 sin²x cos²x - 12 sinx cos²x - 2 cos²x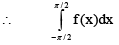
 

Q.14. The value of 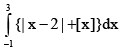(where [x] stands for greatest integer less than or equal to x), is

Ans. 7

Q.15. If x = 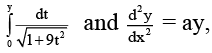then 'a' is

Ans. 9