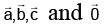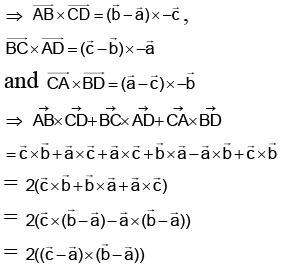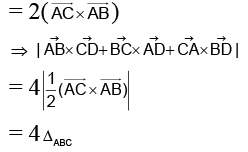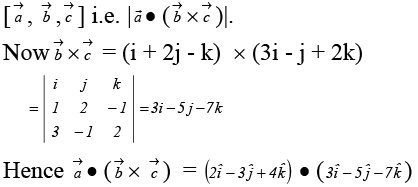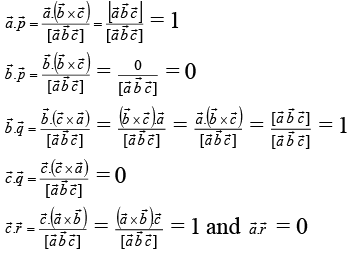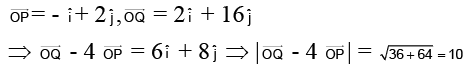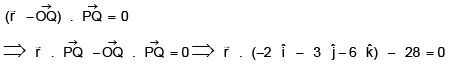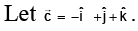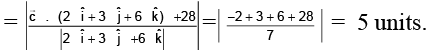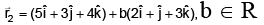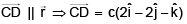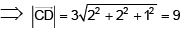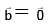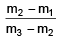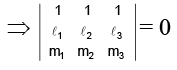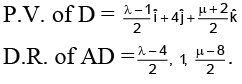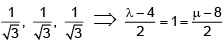Integer Answer Type Questions for JEE: Vector Algebra | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. A, B, C and D are any four points in the space. If 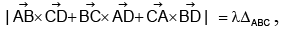 where ΔABC is the area of triangle ABC, then λ is equal to:
where ΔABC is the area of triangle ABC, then λ is equal to:
Ans. 4
Let P.V. of A, B, C and D be
Q.2. The vectors 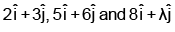 have their initial points at (1, 1), the value of λ so that the vectors terminate on one straight line is
have their initial points at (1, 1), the value of λ so that the vectors terminate on one straight line is
Ans. 9
Since initial point oftheir terminal points will be
Now given all the vectors terminate on one straight line. Hence
⇒ λ1 = 1 and λ = 9
Q.3. Find the volume of the paralleopiped whose edges are represented by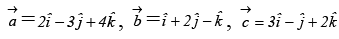
Ans. 7
The required volume of the parallelopiped is equal to the absolute value of
= 6 + 15 - 28 = -7
Neglecting the negative sign, we get the volume of the parallelopiped = 7.
Q.4. Let 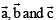 be three non-coplanar vectors, and let
be three non-coplanar vectors, and let  be the vectors defined by the relations
be the vectors defined by the relations 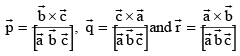
Then the value of the expression 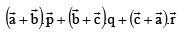 is equal to
is equal to
Ans. 3
Therefore, the given expression is equal to 1 + 0 + 1 + 0 + 1 + 0 = 3.
Q.5. The number of vectors of unit length perpendicular to vectors a Ξ (1, 1, 0) and b Ξ (0, 1, 1) is
Ans. 2
The vector of unit length perpendicular to the given vectors
Hence, there are two such vectors.
Q.6. Two given points P and Q in the rectangular cartesian coordinates lie on y = 2x + 2 such that 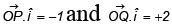 where î is a unit vector along the x - axis. Find the magnitude of
where î is a unit vector along the x - axis. Find the magnitude of 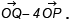
Ans. 10
Let P(x1, y1), Q(x2, y2) be the two points on y = 2x+2projection of
on x – axis, so x1 = -1 ⇒ y1 = 2
projection of
on x – axis, so x2 = 2 ⇒ y2 = 16
Ifis a unit vector along y– axis, then
Q.7. Given that 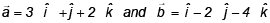 are the position vectors of points P and Q respectively. Find the equation for the plane passing through Q and perpendicular to the line PQ. What is the distance from the point (-1, 1, 1) to the plane?
are the position vectors of points P and Q respectively. Find the equation for the plane passing through Q and perpendicular to the line PQ. What is the distance from the point (-1, 1, 1) to the plane?
Ans. 5
Equation of plane passing through Q and perpendicular to PQ is.....(1)
Hence, distance fromthe plane (1) is
Q.9. Line L1 is parallel to a vector 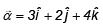 and passes through a point A (7,6,2) and the line L2 is parallel to a vector
and passes through a point A (7,6,2) and the line L2 is parallel to a vector 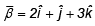 and passes through a point B (5, 3,4). Now a line L3 parallel to a vector
and passes through a point B (5, 3,4). Now a line L3 parallel to a vector 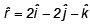 intersects the lines L1 and L2 at points C and D respectively. Find
intersects the lines L1 and L2 at points C and D respectively. Find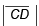 .
.
Ans. 9
P.V. of C.
P.V.of D,and we know that
Hence, by comparing bothwe get 3a + 2b – 2c = 2-2a + b+ 2c = 3
⇒ -4a + 3b + c = - 2 ⇒ a = 2, b = 1, c = 3
Q.9. 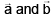 are two non-collinear vectors then the points with position vectors
are two non-collinear vectors then the points with position vectors 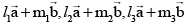 are collinear if
are collinear if 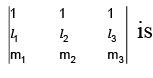 _______.
_______.
Ans. 0
Given points will be collinear if
(ℓ2 - ℓ1)+ (m2 - m1) b = λ [(ℓ3 - ℓ2)
+(m3 - m2)
]
or, [ℓ2 - ℓ1 - λ (ℓ3 - ℓ2)]+ [(m2 - m1) - λ (m3 - m2)]
As, are non-collinear,
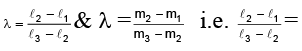
⇒ (ℓ2 - ℓ1) (m3 - m2) = (m2 - m1) (ℓ3 - ℓ2)
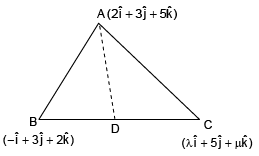
Q.10. Let 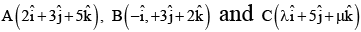 are vertices of a triangle and its median through A is equally inclined to the positive directions of the axes. The value of 2λ - μ is equal to _______.
are vertices of a triangle and its median through A is equally inclined to the positive directions of the axes. The value of 2λ - μ is equal to _______.
Ans. 2
But direction ratios of Ad should be
λ = 6, μ = 10
2λ - μ = 2.
|
446 docs|930 tests
|