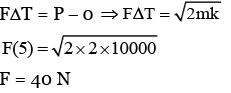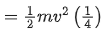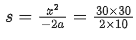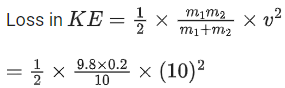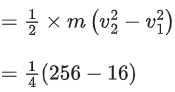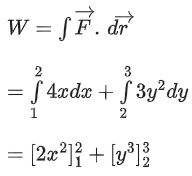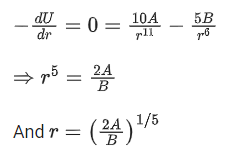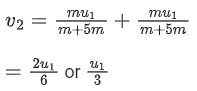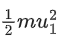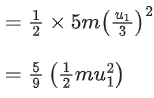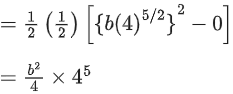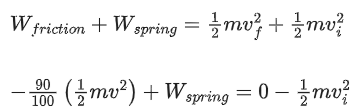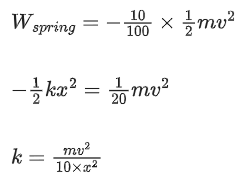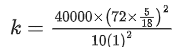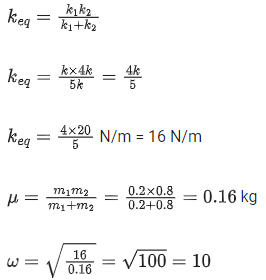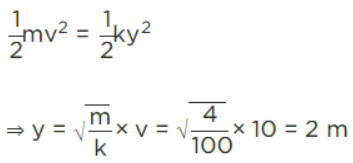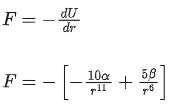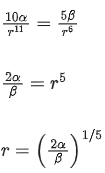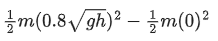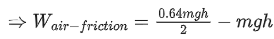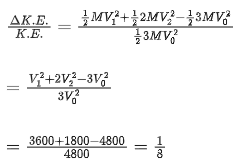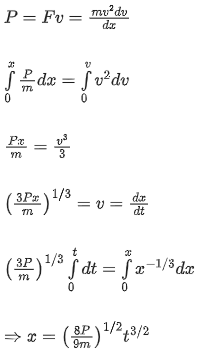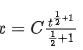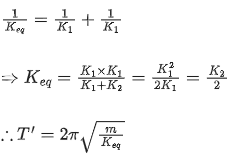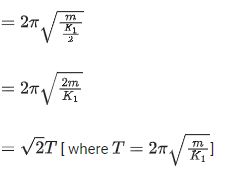JEE Main Previous year questions (2021-23): Work, Energy and Power PDF Download

Q.1. A spherical body of mass 2 kg starting from rest acquires a kinetic energy of 10000 J at the end of 5th second. The force acted on the body is ______ N.    (JEE Main 2023)

Ans. 40
Impulse = ΔP

Q.2. A ball is projected with kinetic energy E, at an angle of 60^∘ to the horizontal. The kinetic energy of this ball at the highest point of its flight will become :    (JEE Main 2022)
(a) Zero
(b) E/2
(c) E/4
(d) E

Ans. c
K.E. = E = 1/2mv²
at highest point
K.E′ = 1/2mv²cos²θ

= E/4

Q.3. A bullet of mass 200 g having initial kinetic energy 90 J is shot inside a long swimming pool as shown in the figure. If it's kinetic energy reduces to 40 J within 1 s, the minimum length of the pool, the bullet has to travel so that it completely comes to rest is    (JEE Main 2022)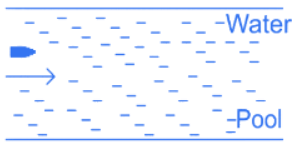
(a) 45 m
(b) 90 m
(c) 125 m
(d) 25 m

Ans. a

12mx² = 90
⇒ 12 × 0.2 × x² = 90,
x² = 900
x=30 m/s
12mv² = 40 ⇒ v = 2/3 × 30 = 20 m/s
20 = 30 − α × 1 ⇒ α = −10 m/s²
0 − x² = 2αs

= 45 m

Q.4. Sand is being dropped from a stationary dropper at a rate of 0.5kgs⁻¹ on a conveyor belt moving with a velocity of 5 ms⁻¹. The power needed to keep the belt moving with the same velocity will be :    (JEE Main 2022)
(a) 1.25 W
(b) 2.5 W
(c) 6.25 W
(d) 12.5 W

Ans. d
dm/dt = 0.5 kg/s
v = 5 m/s
F = vdm/dt = 2.5 kg m/s²
=(2.5)(5) W
= 12.5 W

Q.5. As per the given figure, two blocks each of mass 250 g are connected to a spring of spring constant 2Nm⁻¹. If both are given velocity v in opposite directions, then maximum elongation of the spring is :    (JEE Main 2022)
(a) v/2√2
(b) v/2
(c) v/4
(d) v/√2

Ans. b
∵ Loss in KE = Gain in spring energy

Q.6. A bag of sand of mass 9.8 kg is suspended by a rope. A bullet of 200 g travelling with speed 10 ms⁻¹ gets embedded in it, then loss of kinetic energy will be :    (JEE Main 2022)
(a) 4.9 J
(b) 9.8 J
(c) 14.7 J
(d) 19.6 J

Ans. b

= 9.8 J

Q.7. A body of mass 0.5 kg travels on straight line path with velocity v = (3x² + 4)m/s. The net work done by the force during its displacement from x = 0 to x = 2 m is :    (JEE Main 2022)
(a) 64 J
(b) 60 J
(c) 120 J
(d) 128 J

Ans. b
v = 3x² + 4
at x = 0, v₁ = 4 m/s
x = 2, v₂ = 16 m/s
⇒ Work done = Δ kinetic energy

= 60 J

Q.8. A particle experiences a variable force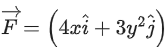in a horizontal x-y plane. Assume distance in meters and force is newton. If the particle moves from point (1, 2) to point (2, 3) in the x-y plane, then Kinetic Energy changes by :    (JEE Main 2022)
(a) 50.0 J
(b) 12.5 J
(c) 25.0 J
(d) 0 J

Ans. c

= 2 × 3 + (27 − 8)
= 25 J

Q.9. Potential energy as a function of r is given by  where r is the interatomic distance, A and B are positive constants. The equilibrium distance between the two atoms will be:    (JEE Main 2022)
(a)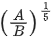
(b)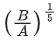
(c)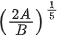
(d)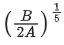

Ans. c
For equilibrium

Q.10. What percentage of kinetic energy of a moving particle is transferred to a stationary particle when it strikes the stationary particle of 5 times its mass?
(Assume the collision to be head-on elastic collision)    (JEE Main 2022)
(a) 50.0%
(b) 66.6%
(c) 55.6%
(d) 33.3%

Ans. c
For a head on elastic collision

Initial kinetic energy of first mass =
Final kinetic energy of second mass

⇒ kinetic energy transferred = 55% of initial kinetic energy of first colliding mass.

Q.11. A lead bullet penetrates into a solid object and melts. Assuming that 40% of its kinetic energy is used to heat it, the initial speed of bullet is :
(Given : initial temperature of the bullet = 12^∘C, Melting point of the bullet = 32^∘C, Latent heat of fusion of lead = 2.5 × 10⁴ J kg⁻¹, Specific heat capacity of lead = 125 J/kg K)    (JEE Main 2022)
(a) 125 ms⁻¹
(b) 500 ms⁻¹
(c) 250 ms⁻¹
(d) 600 ms⁻¹

Ans. b
= mL + msΔT
⇒ v²/5 = 2.5 × 10⁴ + 125 + 200
⇒ v²/5 = 5 × 10⁴
⇒ v = 500 m/s

Q.12. In the given figure, the block of mass m is dropped from the point 'A'. The expression for kinetic energy of block when it reaches point 'B' is    (JEE Main 2022)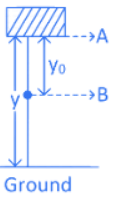
(a)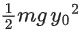
(b)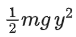
(c) mg(y−y₀)
(d) mgy₀

Ans. d
Loss in potential energy = gain in kinetic energy
− (mg(y − y₀) − mgy) = KE − 0
⇒ KE = mgy₀

Q.13. A particle of mass 500 gm is moving in a straight line with velocity v = b x^5/2. The work done by the net force during its displacement from x = 0 to x = 4 m is : (Take b = 0.25 m^−3/2 s⁻¹)    (JEE Main 2022)
(a) 2 J
(b) 4 J
(c) 8 J
(d) 16 J

Ans. d
W_total = ΔK

W_total = 16 J

Q.14. Arrange the four graphs in descending order of total work done; where W₁, W₂, W₃ and W₄ are the work done corresponding to figure a, b, c and d respectively.    (JEE Main 2022)
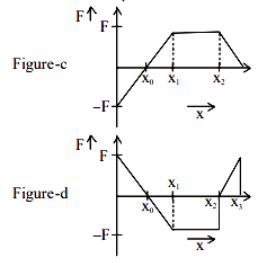(a) W₃ > W₂ > W₁ > W₄
(b) W₃ > W₂ > W₄ > W₁
(c) W₂ > W3 > W4 > W₁
(d) W₂ > W₃ > W₁ > W₄

Ans. a
W_a = 0, W_b = +ve, W_c = +ve > W_b, W_d = −ve
⇒ W_c > W_b > W_a > W_d
⇒ W₃ > W₂ > W₁ > W₄

Q.15. A uniform chain of 6 m length is placed on a table such that a part of its length is hanging over the edge of the table. The system is at rest. The co-efficient of static friction between the chain and the surface of the table is 0.5, the maximum length of the chain hanging from the table is ___________ m.    (JEE Main 2022)

Ans. 2
(x)gλ = μ(6−x)gλ where x is length of hanging part
⇒ x = 3 − 0.5x
⇒ x = 2 m

Q.16. An engine is attached to a wagon through a shock absorber of length 1.5 m. The system with a total mass of 40,000 kg is moving with a speed of 72 kmh⁻¹ when the brakes are applied to bring it to rest. In the process of the system being brought to rest, the spring of the shock absorber gets compressed by 1.0 m. If 90% of energy of the wagon is lost due to friction, the spring constant is ____________ × 10⁵ N/m.    (JEE Main 2021)

Ans. 16

Given, the length of the shock absorber, l = 1.5 m
The total mass of the system, M = 40000 kg
The speed of the wagon, v = 72 km/h
When brakes are applied, the final velocity, vf = 0
The compressed spring of the shock absorber, x = 1 m
Applying the work-energy theorem,
Work done by the system = Change in kinetic energy
W = ΔKE

(∵ 90% energy lost due to friction)

Substituting the values in the above equation, we get

= 16 × 10⁵ N/m
Comparing the spring constant, k = x × 10⁵
The value of the x = 16.

Q.17. A block moving horizontally on a smooth surface with a speed of 40 ms⁻¹ splits into two equal parts. If one of the parts moves at 60 ms⁻¹ in the same direction, then the fractional change in the kinetic energy will be x : 4 where x = ___________.    (JEE Main 2021)

Ans. 1

P_i = P_f
m × 40 = m/2 × v + m/2 × 60
40 = v/2 + 30
⇒ v = 20
(K. E.)_I = 1/2m × (40)² = 800 m
(K. E.)_f = 1/2m/2 . (20)² + 1/2 . m/2 (60)² = 1000 m
| Δ K. E. | = | 1000m − 800 m | = 200 m

x = 1

Q.18. Two persons A and B perform same amount of work in moving a body through a certain distance d with application of forces acting at angle 45^∘ and 60^∘ with the direction of displacement respectively. The ratio of force applied by person A to the force applied by person B is 1/√x. The value of x is _________.    (JEE Main 2021)

Ans. 2
Given W_A = W_B
F_Ad cos45^∘ = F_Bd cos60^∘
F_A × 1√2 = F_B × 1/2
F_A/F_B = √2/2 = 1√2
x = 2

Q.19. A uniform chain of length 3 meter and mass 3 kg overhangs a smooth table with 2 meter lying on the table. If k is the kinetic energy of the chain in joule as it completely slips off the table, then the value of k is _________. (Take g = 10 m/s²)    (JEE Main 2021)

Ans. 40

From energy conservation
K_i + U_i = k_f + U_f
0 + (−1 × 10 × 12) = k_f + (−3 × 10 × 3/2)
−5 = k_f − 45
k_f = 40 J

Q.20. A small block slides down from the top of hemisphere of radius R = 3 m as shown in the figure. The height 'h' at which the block will lose contact with the surface of the sphere is __________ m.
(Assume there is no friction between the block and the hemisphere)    (JEE Main 2021)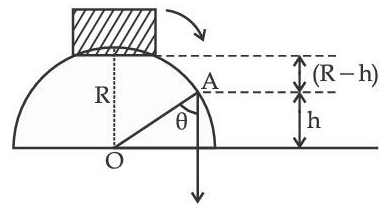

Ans. 2
mg cos ⁡θ = mv²/R .... (1)
cos⁡θ = h/R
Energy conservation
mg{R−h} = 1/2mv² ..... (2)
from (1) & (2)

h = 2R/3 = 2m

Q.21. A force of F =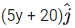N acts on a particle. The work done by this force when the particle is moved from y = 0 m to y = 10 m is ___________ J.    (JEE Main 2021)

Ans. 450

= 5/2 × 100 + 20 × 10
= 250 + 200 = 450 J

Q.22. In the reported figure, two bodies A and B of masses 200 g and 800 g are attached with the system of springs. Springs are kept in a stretched position with some extension when the system is released. The horizontal surface is assumed to be frictionless. The angular frequency will be ____________ rad/s when k = 20 N/m.    (JEE Main 2021)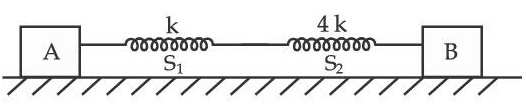

Ans. 10
ω =
μ = reduced mass
springs are in series connection

Q.23. A ball of mass 4 kg, moving with a velocity of 10 ms⁻¹, collides with a spring of length 8 m and force constant 100 Nm⁻¹. The length of the compressed spring is x m. The value of x, to the nearest integer, is ____________.    (JEE Main 2021)

Ans. 6
Let the spring is compressed by y.
Applying energy conservation principle,

Therefore, final length of the spring = 8 − 2 = 6m

Q.24. As shown in the figure, a particle of mass 10 kg is placed at a point A. When the particle is slightly displaced to its right, it starts moving and reaches the point B. The speed of the particle at B is x m/s. (Take g = 10 m/s²)
The value of 'x' to the nearest integer is __________.    (JEE Main 2021)

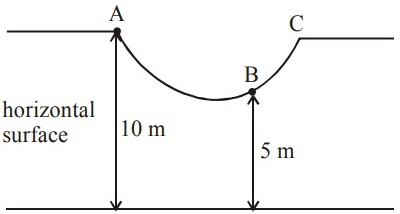
Ans. 10
By energy conservation
K_i + U_i = K_f + U_f
0 + 10 × 10 × 10 = 1/2 × 10 ×  + 10 × 10 × 5
1000 =  + 500
 = 500/5 = 100
V_B = 10 m/s
x = 10

Q.25. A boy pushes a box of mass 2 kg with a force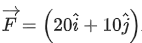N on a frictionless surface. If the box was initially at rest, then ___________ m is displacement along the x-axis after 10s.    (JEE Main 2021)

Ans. 500

∴ Displacement along x-axis
= 50 × 10 = 500 m

Q.26. The potential energy (U) of a diatomic molecule is a function dependent on r (interatomic distance) as
U = α/r¹⁰− β/r⁵ − 3
where, α and β are positive constants. The equilibrium distance between two atoms will be 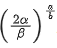, where a = ___________.    (JEE Main 2021)

Ans. 1

for equilibrium, F = 0

∴ α = 1

Q.27. A body of mass 'm' dropped from a height 'h' reaches the ground with a speed of 0.8gh. The value of workdone by the air-friction is :    (JEE Main 2021)
(a) −0.68 mgh
(b) mgh
(c) 1.64 mgh
(d) 0.64 mgh

Ans. a
Given, the mass of the body = m
The height from which the body dropped = h
The speed of the body when reached the ground, v_f = 0.8 √gh
Initial velocity of the body, v = 0 m/s
Using the work-energy theorem,
Work done by gravity + Work done by air-friction = Final kinetic energy − Initial kinetic energy.
W_mg + W_{air−friction} = 1/2mvf2−12mvi2
Here, work done by gravity = mgh
⇒mgh+Wair−friction =

⇒ 0.32mgh − mgh = −0.68mgh
The value of the work done by the air friction is − 0.68 mgh.

Q.28. A block moving horizontally on a smooth surface with a speed of 40 m/s splits into two parts with masses in the ratio of 1 : 2. If the smaller part moves at 60 m/s in the same direction, then the fractional change in kinetic energy is :-    (JEE Main 2021)
(a) 1/3
(b) 2/3
(c) 1/8
(d) 1/4

Ans. c

3MV₀ = 2MV₂ + MV₁
3V₀ = 2V₂ + V₁
120 = 2V₂ + 60 ⇒ V₂ = 30 m/s

Q.29. An automobile of mass 'm' accelerates starting from origin and initially at rest, while the engine supplies constant power P. The position is given as a function of time by :    (JEE Main 2021)
(a)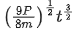
(b)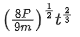
(c)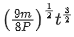
(d)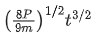

Ans. d
P = const.

Q.30. Given below is the plot of a potential energy function U(x) for a system, in which a particle is in one dimensional motion, while a conservative force F(x) acts on it. Suppose that E_mech = 8 J, the incorrect statement for this system is :    (JEE Main 2021)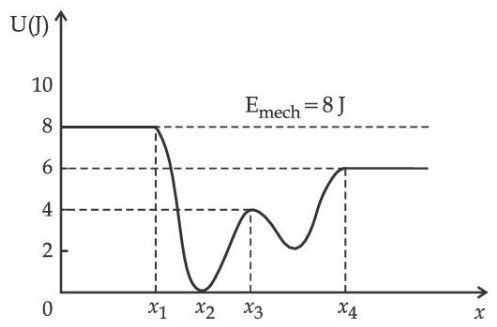
[ where K.E. = kinetic energy ]
(a) at x > x₄ K.E. is constant throughout the region.
(b) at x < x₁, K.E. is smallest and the particle is moving at the slowest speed.
(c) at x = x₂, K.E. is greatest and the particle is moving at the fastest speed.
(d) at x = x₃, K.E. = 4 J.

Ans. b
Emech. = 8J
(A) at x > x₄
U = constant = 6J
K = E_mech. − U = 2J = constant
(B) at x < x₁
U = constant = 8J
K = E_mech − U = 8 − 8 - 0 J
Particle is at rest.
(C) At x = x₂,
U = 0 ⇒ E_mech. = K = 8 J
KE is greatest, and particle is moving at fastest speed.
(D) At x = x₃
U = 4J
U + K = 8J
K = 4J

Q.31. A porter lifts a heavy suitcase of mass 80 kg and at the destination lowers it down by a distance of 80 cm with a constant velocity. Calculate the work done by the porter in lowering the suitcase.
(take g = 9.8 ms⁻²)    (JEE Main 2021)
(a) +627.2 J
(b) −62720.0 J
(c) −627.2 J
(d) 784.0 J

Ans. c
W = −N × Δx
=−80 × 9.8 × 80/100
= −627.2 J

Q.32. A body at rest is moved along a horizontal straight line by a machine delivering a constant power. The distance moved by the body in time 't' is proportional to :    (JEE Main 2021)
(a) t^3/2
(b) t^1/2
(c) t^1/4
(d) t^3/4

Ans. a
P = constant
1/2mv² = Pt
⇒ v ∝ √t
dx/dt = C√t [C = constant]
by integration.

x ∝ t^3/2

Q.33. A constant power delivering machine has towed a box, which was initially at rest, along a horizontal straight line. The distance moved by the box in time 't' is proportional to :-    (JEE Main 2021)
(a) t2/3
(b) t3/2
(c) t
(d) t^1/2

Ans. b
P = F.v = mav
P =  mvdv/dt

x ∝ t^3/2

Q.34. A boy is rolling a 0.5 kg ball on the frictionless floor with the speed of 20 ms^-1. The ball gets deflected by an obstacle on the way. After deflection it moves with 5% of its initial kinetic energy. What is the speed of the ball now?    (JEE Main 2021)
(a) 14.41 ms⁻¹
(b) 19.0 ms⁻¹
(c) 4.47 ms⁻¹
(d) 1.00 ms⁻¹

Ans. c
K.E_.f = 5%KE_i
12mv² = 5/100 × 1/2 × m × 20²
v2 = 1/20 x 20² = 20
v = √20 = 2/5 m/s
= 4.47 m/s

Q.35. If two similar springs each of spring constant K1 are joined in series, the new spring constant and time period would be changed by a factor :    (JEE Main 2021)
(a) 12, 2√2
(b) 14, 2√2
(c) 12, √2
(d) 14, √2

Ans. c