JEE Main Previous year questions (2021-23): Complex Numbers PDF Download

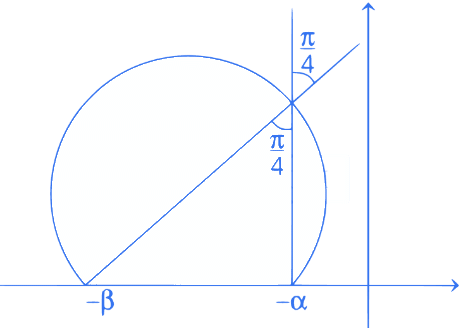
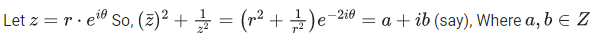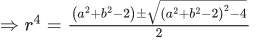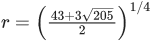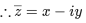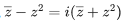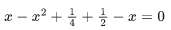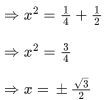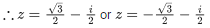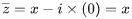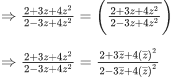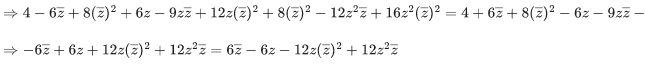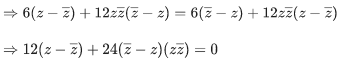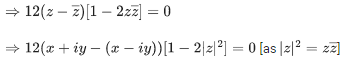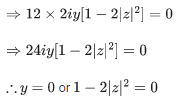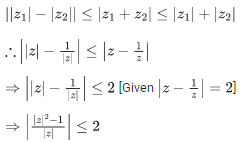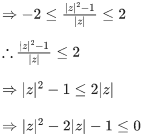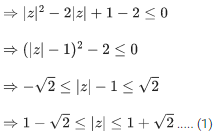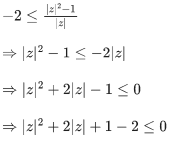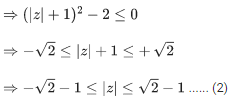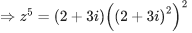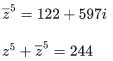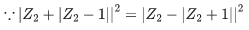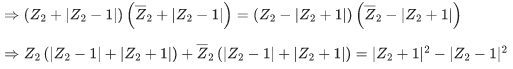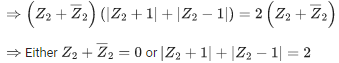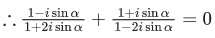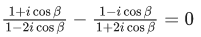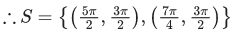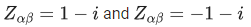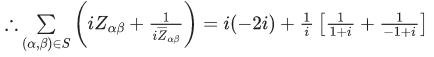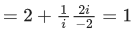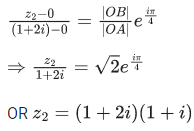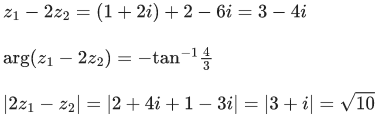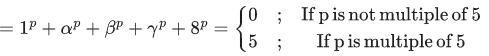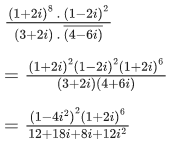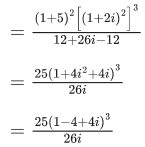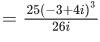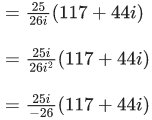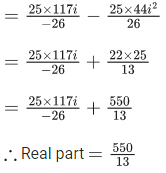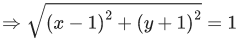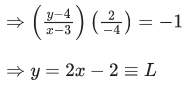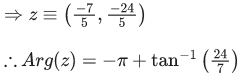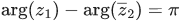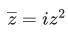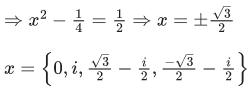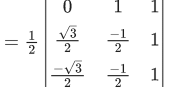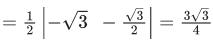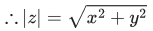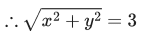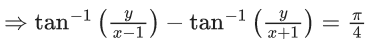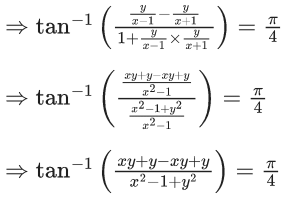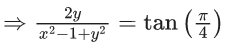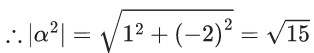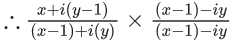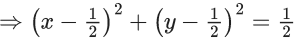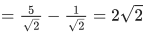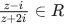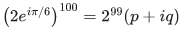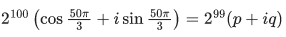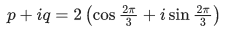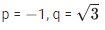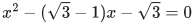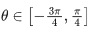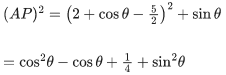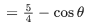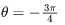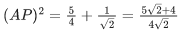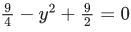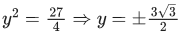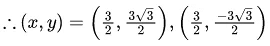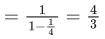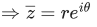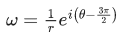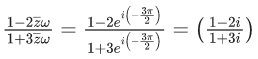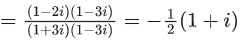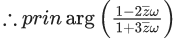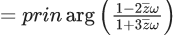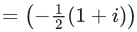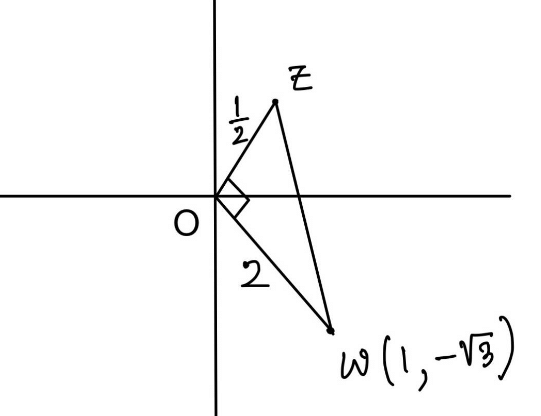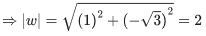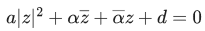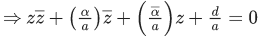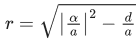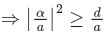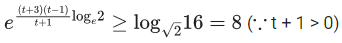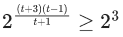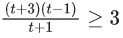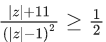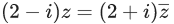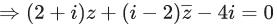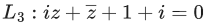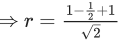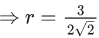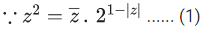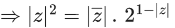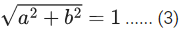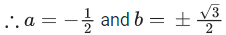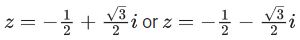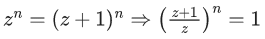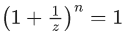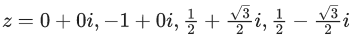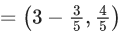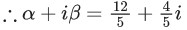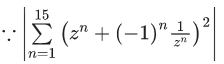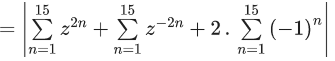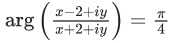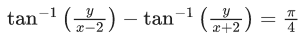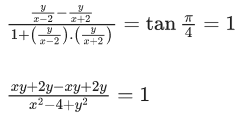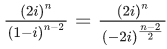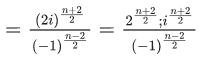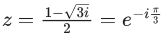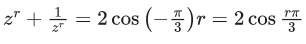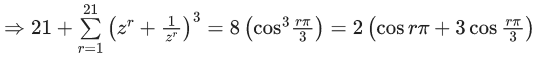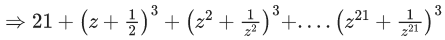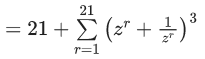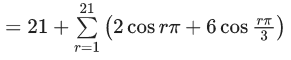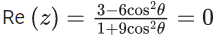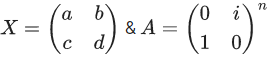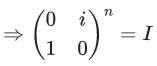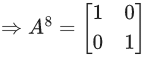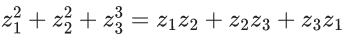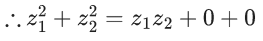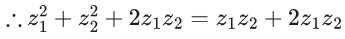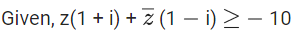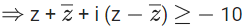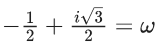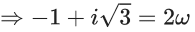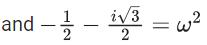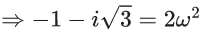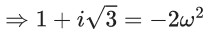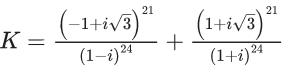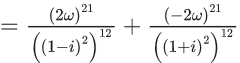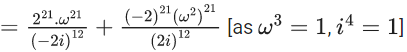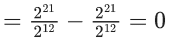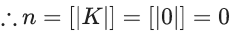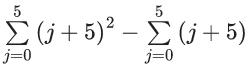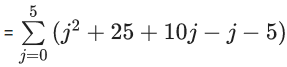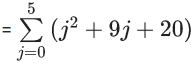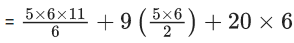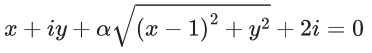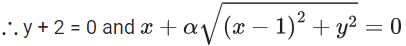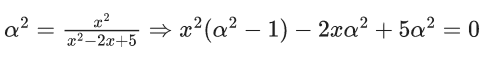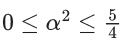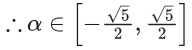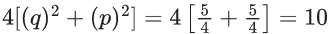Q.1. Let p, q ∈ ℝ and (1 − √3i)²⁰⁰ = 2¹⁹⁹(p + iq), i = √−1 Then p + q + q² and p − q + q² are roots of the equation        (JEE Main 2023)
(a) x² − 4x − 1 = 0
(b) x² − 4x + 1 = 0
(c) x² + 4x − 1 = 0
(d) x² + 4x + 1 = 0

Ans. b

⇒  p = -1, q = - √3
Now
α = p + q + q² = 2-√3
β = p - q + q² = 2 + √3
req. quad is x² - 4x + 1 = 0

Q.2. Let 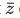 denote the complex conjugate of a complex number z. If z is a non-zero complex number for which both real and imaginary parts of 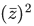+(1/z²) are integers, then which of the following is/are possible value(s) of |z| ?    (JEE Advanced 2022)
(a)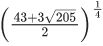
(b)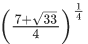
(c)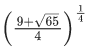
(d)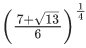

Ans. a

So, (r²+(1/r²))² = a²+b²
⇒ r⁸−(a²+b²−2)r⁴+1 = 0

For a²+b² = 45
i.e (a, b) = (±6,±3) or (±3,±6)
We get

Q.3. Let 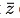  denote the complex conjugate of a complex number z and let i= 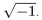In the set of complex numbers, the number of distinct roots of the equation  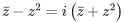is _________.    (JEE Advanced 2022)

Ans. 4
Let, z = x+iy

Given,
⇒ (x−iy)−(x+iy)² = i[(x−iy)+(x+iy)²]
⇒ (x−iy)−(x²−y²+2ixy) = i[x−iy+x²−y²+2ixy]
⇒ (x−x²+y²)−iy(1+2x) = xi−i²y+x²i−iy²+2i²xy
⇒ (x−x²+y²)−iy(1+2x) = xi+y+ix²−iy²−2xy
⇒ (x−x²+y²)−iy(1+2x) = y(1−2x)+i(x+x²−y²)
Comparing both sides real part we get,
x−x²+y² = y−2xy
⇒ x−x²+y²−y+2xy = 0 ..... (1)
And comparing both sides imaginary part we get,
−y(1+2x) = x+x²−y²
⇒ −y−2xy = x+x²−y²
⇒ x+x²−y²+y+2xy = 0 ...... (2)
Adding equation (1) and (2) we get,
x−x²+y²−y+2xy+x+x²−y²+y+2xy = 0
⇒ 2x+4xy = 0
⇒2x(1+2y) = 0
∴ x = 0 or 1+2y = 0 ⇒ y =−(1/2)
Case 1 : When x = 0 :
Put x = 0 at equation (1), we get
y²−y = 0
⇒ y(y−1) =0
⇒ y = 0,1
∴ z = 0+0i or 0+i
Case 2 : When y = −(1/2) :
Put y = −(1/2) in equation (1), we get



∴ Number of distinct z = 4

Q.4.  Let z be a complex number with a non-zero imaginary part. If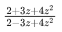

is a real number, then the value of |z|² is _________.    (JEE Advanced 2022)

Ans. 0.49 and 0.51
For a complex number z = x+iy, it's conjugate  Now z is purely real when y=0.
When y = 0 then z = x + i × (0) = x and
∴  when z is purely real.
Now given,  is real






y = 0 not possible as given z is a complex number with non-zero imaginary part.
∴ 1−2|z|² = 0
⇒ |z|² = 1/2 = 0.5

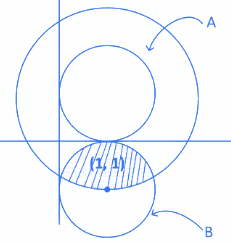
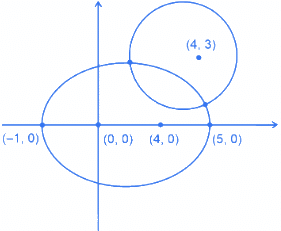
Q.5. Let S = {z = x+iy: |z−1+i| ≥ |z|, |z|<2, |z+i| = |z−1|}. Then the set of all values of x, for which w=2x+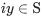 for some 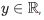, is    (JEE Main 2022)
(a)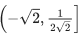
(b)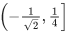
(c)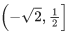
(d)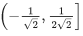

Ans. b

Q.6. If z ≠ 0 be a complex number such that |z − (1/z)|=2, then the maximum value of |z| is :    (JEE Main 2022)
(a) √2
(b) 1
(c) √2−1
(d) √2+1

Ans. d
We know,



or


From (1) and (2) we get,
Maximum value of |z| = √2+1 and minimum value of |z| = -√2-1

Q.7. If z=2+3i, then 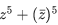 is equal to :    (JEE Main 2022)
(a) 244
(b) 224
(c) 245
(d) 265

Ans. a
z = (2 + 3i)

= (2+3i)(−5+12i)²
= (2+3i)(−119−120i)
= −238−240i−357i+360
= 122−597i

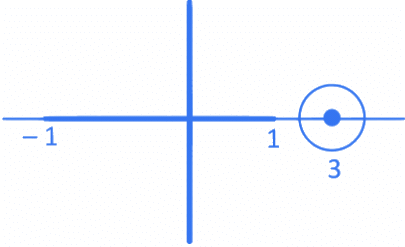
Q.8. Let S₁ = {z₁ ∈ C:|z₁−3|=1/2} and S₂ = {z₂ ∈ C:|z₂−|z₂+1||=|z₂+|z₂−1||}. Then, for z₁ ∈ S₁ and z₂ ∈ S₂, the least value of |z₂−z₁| is :    (JEE Main 2022)
(a) 0
(b) 1/2
(c) 3/2
(d) 5/2

Ans. c



So, Z₂ lies on imaginary axis or on real axis within [-1, 1]
Also |Z₁−3| = 1/2 ⇒ Z₁ lies on the circle having center 3 and radius 1/2.

Clearly |Z₁ - Z₂|_min = 3/2.

Q.9. Let S be the set of all (α, β),π<α, β<2π, for which the complex number 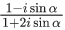 is purely imaginary and  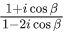is purely real. Let Z_αβ = sin⁡2α + icos⁡2β,(α,β) ∈ S. Then  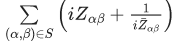is equal to :    (JEE Main 2022)
(a) 3
(b) 3i
(c) 1
(d) 2 - i

Ans. c
 is purely imaginary

⇒ 1- 2sin²α = 0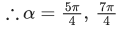
 
and  is purely real

⇒ cos⁡β = 0
∴ β  = 3π/2

Q.10. Let the minimum value v₀ of v=|z|²+|z−3|²+|z−6i|²,  is attained at z=z₀. Then 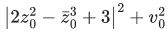 is equal to    (JEE Main 2022)
(a) 1000
(b) 1024
(c) 1105
(d) 1196

Ans. a
Let z = x+iy
v = x²+y²+(x−3)²+y²+x²+(y−6)²
= (3x²−6x+9)+(3y²−12y+36)
= 3(x²+y²−2x−4y+15)
= 3[(x−1)²+(y−2)²+10]
v_min at z =1+2i = z₀ and v₀ = 30
so |2(1+2i)²−(1−2i)³+3|²+900
= |2(−3+4i)−(1−8i³−6i(1−2i)+3|²+900
= |−6+8i−(1+8i−6i−12)+3|²+900
= |8+6i|²+900
= 1000

Q.11. If z = x+iy satisfies |z|−2 = 0 and |z−i|−|z+5i| = 0, then    (JEE Main 2022)
(a) x + 2y - 4 = 0
(b) x² + y - 4 = 0
(c) x + 2y + 4 = 0
(d) x² - y + 3 = 0

Ans. c
|z−i| = |z+5i|
So, z lies on ⊥^r bisector of (0,1) and (0,−5)
i.e., line y = −2
as |z| = 2
⇒ z = −2i
x = 0 and y = −2
so, x+2y+4 = 0

Q.12. Let O be the origin and A be the point z₁=1+2i. If B is the point z₂, Re(z₂)<0, such that OAB is a right angled isosceles triangle with OB as hypotenuse, then which of the following is NOT true?    (JEE Main 2022)
(a) arg⁡z₂ = π−tan⁻¹3
(b) arg⁡(z₁−2z₂) = −tan⁻¹₍4/3)
(c) |z₂| = √10
(d) |2z₁−z₂| = 5

Ans. d

Q.13. For z ∈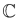 if the minimum value of (|z−3√2|+|z−p√2i|) is 5√2, then a value Question: of p is  _________.    (JEE Main 2022)
(a) 3
(b) 7/2
(c) 4
(d) 9/2

Ans. c

It is sum of distance of z from (3√2, 0) and (0, p√2)
For minimising, z should lie on AB and AB = 5√2
(AB)² = 18+2p²
p = ±4

Q.14. For n∈N, let S_n={z∈C:|z−3+2i| = n/4} and T_n = {z∈C:|z−2+3i| = 1/n}. Then the number of elements in the set {n ∈ N : S_n ∩ T_n = ϕ} is :    (JEE Main 2022)
(a) 0
(b) 2
(c) 3
(d) 4

Ans. d

Q.15. If α, β, γ, δ are the roots of the equation x⁴ + x³ + x² + x + 1 = 0, then α²⁰²¹ + β²⁰²¹ + γ²⁰²¹ + δ²⁰²¹ is equal to :    (JEE Main 2022)
(a) -4
(b) -1
(c) 1
(d) 4

Ans. b
When, x⁵ = 1
then x⁵−1 = 0
⇒ (x−1)(x⁴+x³+x²+x+1) = 0
Given, x⁴+x³+x²+x+1 = 0 has roots α, β, γ and 8.
∴ Roots of x⁵−1 = 0 are 1, α, β, γ and 8.
We know, Sum of p^th power of n^th roots of unity = 0. (If p is not multiple of n) or n (If p is multiple of n)
∴ Here, Sum of p^th power of n^th roots of unity

Here, p = 2021, which is not multiple of 5.
∴ 1²⁰²¹ + α²⁰²¹ + β²⁰²¹ + γ²⁰²¹ + 8²⁰²¹ = 0

⇒ α²⁰²¹ + β²⁰²¹ + γ²⁰²¹ + 8²⁰²¹  = -1.

Q.16. The real part of the complex number 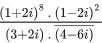 is equal to :    (JEE Main 2022)
(a) 500/13
(b) 110/13
(c) 55/6
(d) 550/13

Ans. d
Given,

Q.17. Let A={z∈C:1≤|z−(1+i)|≤2} and B={z∈A:|z−(1−i)|=1}. Then, B :    (JEE Main 2022)
(a) is an empty set
(b) contains exactly two elements
(c) contains exactly three elements
(d) is an infinite set

Ans. d
Let, z = x+iy
Given, 1 ≤ |z−(1+i)| ≤ 2
⇒ 1 ≤ |x+iy−1−i| ≤ 2
⇒ 1 ≤ |(x−1)+i(y−1)| ≤ 2
⇒ 1≤≤2
It represent two concentric circle both have center at (1, 1) and radius 1 and 2.

Also given,
|z−(1−i)| = 1
⇒ |x+iy−1+i| = 1
⇒ |(x−1)+i(y+1)| = 1

This represent a circle with center at (1, −1) and radius = 1.

In the common region infinite values of B possible.

Q.18. Let a circle C in complex plane pass through the points z₁=3+4i, z₂=4+3i and z₃=5i. If z(≠z₁) is a point on C such that the line through z and z₁ is perpendicular to the line through z₂ and z₃, then arg(z) is equal to:    (JEE Main 2022)
(a)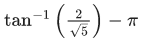
(b)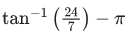
(c)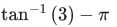
(d)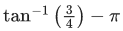

Ans. b
z₁ = 3+4i, z₂ = 4+3i and z₃ = 5i
Clearly, C ≡ x²+y² = 25
Let  z(x, y)

∴ z is intersection of C & L

Q.19. Let z₁ and z₂ be two complex numbers such that 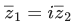 and 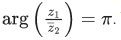 Then    (JEE Main 2022)
(a) arg⁡ z₂ =  π/4
(b) arg⁡ z₂ = −(3π/4)
(c) arg⁡ z₁ = π/4
(d) arg ⁡z₁ = −(3π/4)

Ans. c
∵ (z₁/z₂) = −i  ⇒ z₁ = −iz₂
⇒ arg⁡(z₁) = −(π/2) + arg⁡(z₂) ..... (i)
Also
⇒ arg⁡(z₁)+arg⁡(z₂) = π ..... (ii)
From (i) and (ii), we get
arg⁡(z₁) = π/4 and arg⁡(z₂) = 3π/4.

Q.20. Let 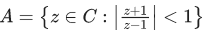 and 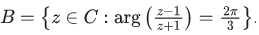 Then A ∩ B is :    (JEE Main 2022)
(a) a portion of a circle centred at (0,−(1√3)) that lies in the second and third quadrants only
(b) a portion of a circle centred at (0,−(1√3)) that lies in the second quadrant only
(c) an empty
(d) a portion of a circle of radius (2/√3) that lies in the third quadrant only

Ans. b

Q.21. The area of the polygon, whose vertices are the non-real roots of the equation 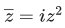is:    (JEE Main 2022)
(a)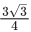
(b)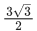
(c) 3/2
(d) 3/4

Ans. a

Let z = x+iy
x−iy = i(x²−y²+2xiy)
x−iy = i(x²−y²)−2xy
∴ x = −2yx or x²−y² = −y
x = 0 or y = −(1/2)
Case - I
x = 0
−y² =  −y
y = 0, 1
Case - II
y = -(1/2)

Area of polygon

Q.22. The number of points of intersection of |z−(4+3i)| = 2 and |z| + |z−4| = 6, z ∈ C, is    (JEE Main 2022)
(a) 0
(b) 1
(c) 2
(d) 3

Ans. c
C₁ : |z−(4+3i)| = 2 and C₂ : |z|+|z−4| = 6, z ∈ C
C₁ represents a circle with centre (4, 3) and radius 2 and C₂ represents a ellipse with focii at (0, 0) and (4, 0) and length of major axis = 6, and length of semi-major axis 2√5 and (4, 2) lies inside the both C₁ and C₂ and (4, 3) lies outside the C₂

∴ number of intersection points = 2

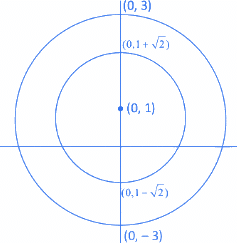
Q.23. Let arg(z) represent the principal argument of the complex number z. Then, |z| = 3 and arg(z − 1) − arg(z + 1) = π/4 intersect    (JEE Main 2022)
(a) exactly at one point.
(b) exactly at two points.
(c) no where.
(d) at infinitely many points.

Ans. c
Let z = x+iy

Given, |z| = 3

⇒ x²+y²=9=3²
This represent a circle with center at (0, 0) and radius = 3

Now, given
⇒ arg⁡(z−1)−arg⁡(z+1) = π/4
⇒ arg⁡(x+iy−1)−arg⁡(x+iy+1) = π/4
⇒ arg⁡(x−1+iy)−arg⁡(x+1+iy) = π/4



⇒ 2y = x²+y²−1
⇒ x²+y²−2y−1 = 0
⇒ x²+(y−1)² = (√2)²
This represent a circle with center at (0, 1) and radius √2.

From diagram you can see both the circles do not cut anywhere.

Q.24. Let α and β be the roots of the equation x² + (2i − 1) = 0. Then, the value of |α⁸ + β⁸| is equal to:    (JEE Main 2022)
(a) 50
(b) 250
(c) 1250
(d) 1500

Ans. a
Given equation,
x²+(2i−1) = 0
⇒ x² = 1−2i
Let α and β are the two roots of the equation.
As, we know roots of a equation satisfy the equation so
α² = 1−2i
and β² = 1−2i
∴ α² =  β² = 1 - 2i

Now, |α⁸+β⁸|
|α⁸+α⁸|
= 2|α⁸|
= 2|α²|⁴
= 2(√5)⁴
= 2×25
= 50

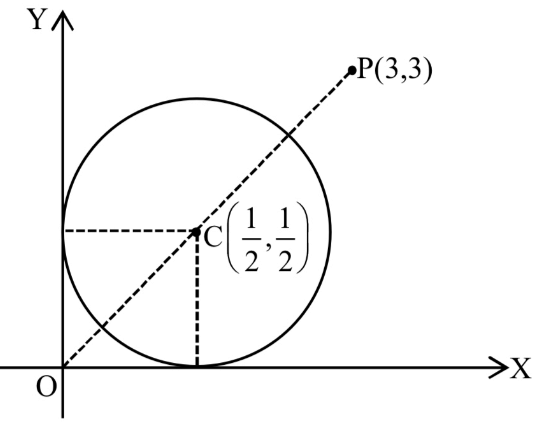
Q.25. If z is a complex number such that 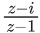 is purely imaginary, then the minimum value of | z − (3 + 3i) | is :    (JEE Main 2021)
(a) 2√2−1
(b) 3√2
(c) 6√2
(d) 2√2

Ans. d
 is purely imaginary number
Let z = x+iy

 is purely imaginary number

⇒ x(x−1)+y(y−1) = 0

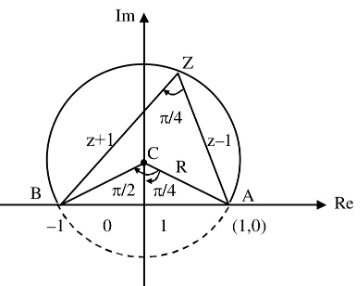
∴ |z−(3+3i)|_min = |PC|−(1/√2)

Q.26. If  then :    (JEE Main 2021)
(a) S contains exactly two elements
(b) S contains only one element
(c) S is a circle in the complex plane
(d) S is a straight line in the complex plane

Ans. d
Given
Then  is 0 or π

⇒ S is straight line in complex

Q.27. If (√3+i)¹⁰⁰ = 2⁹⁹(p+iq), then p and q are roots of the equation :    (JEE Main 2021)
(a) x²−(√3−1)x−√3 = 0
(b) x²+(√3+1)x+√3 = 0
(c) x²+(√3−1)x−√3 = 0
(d) x²−(√3+1)x+√3 = 0

Ans. a

Q.28. The equation 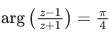 represents a circle with :     (JEE Main 2021)
(a) centre at (0, −1) and radius √2
(b) centre at (0, 1) and radius √2
(c) centre (0, 0) and radius √2
(d) centre at (0, 1) and radius 2

Ans. b

In ΔOAC
sin⁡(π/4) = 1/AC
⇒ AC = √2
Also, tan⁡(π/4) = OA/OC =1/OC
⇒ OC = 1
∴ centre (0, 1); Radius = √2

Q.29. Let C be the set of all complex numbers. Let
S₁ = {z ∈ C||z−3−2i|² = 8}
S₂ = {z ∈ C|Re(z) ≥ 5} and
S₃ = {z ∈ C| ≥ 8}.Then the number of elements in S₁ ∩ S₂ ∩ S₃ is equal to :    (JEE Main 2021)
(a) 1
(b) 0
(c) 2
(d) infinite

Ans. a
S₁:|z−3−2i|² = 8
|z−3−2i| = 2√2
(x−3)²+(y−2)² = (2√2)²
S₂:x ≥ 5
S₃:|| ≥ 8
|2iy| ≥ 8
2|y| ≥ 8
∴ y ≥ 4, y ≤ −4

n(S₁ ∩ S₂ ∩ S₃) =1

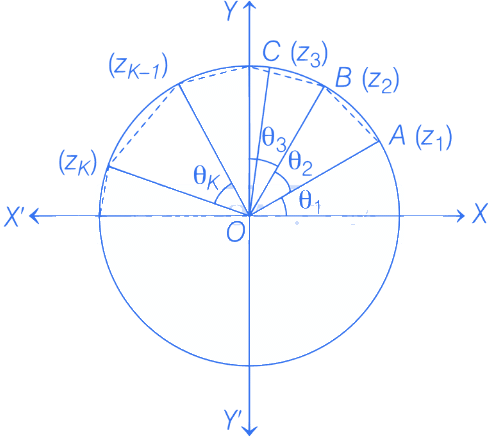
Q.30. Let θ₁, θ₂, ........, θ₁₀ = 2π. Define the complex numbers z₁ = ei^θ1, z_k = z_{k − 1}e^iθk for k = 2, 3, ......., 10, where i = √−1. Consider the statements P and Q given below :    (JEE Advanced 2021)
P:|z₂−z₁| + |z3−z2| +.....+ |z10−z9| + |z1−z10| ≤ 2π
Q:|z₂²−z₁²| + |z₃²−z₂²| +....+ |z₁₀²−z₉²| + |z₁²−z₁₀²| ≤ 4π
Then,
(a) P is TRUE and Q is FALSE
(b) Q is TRUE and P is FALSE
(c) both P and Q are TRUE
(d) both P and Q are FALSE

Ans. c
Both P and Q are true.
∵ Length of direct ditance ≤ length of arc
i.e. |z₂ − z₁| = length of line AB ≤ length of arc AB.

|z₃ − z₂| = length of line BC ≤ length of arc BC.
∴ Sum of length of these 10 lines ≤ sum of length of arcs (i.e. 2π) (because θ1 + θ2 + θ3 + .... + θ10 = 2π given)
∴ |z₂ − z₁| + |z₃ − z₂| + ..... + |z₁ − z₁₀| ≤ 2π → P is true.
And |zk₂ − zk−12| = |zk − zk − 1| |zk + zk − 1|
As we know that,
| z_k + z_{k − 1} | ≤ | z_k | + | z_{k − 1} | ≤ 2
∴ | z₂² − z₁² | + | z₃² − z₂² | + .... + | z₁² − z₁₀² | ≤ 2 ( | z₂ − z₁ | + | z₃ − z₂ | + .... + | z₁ − z₁₀ | )
≤ 2(2π)
≤ 4π → Q is true.

Q.31. For any complex number w = c + id, let arg⁡(ω) ∈ (−π, π], where i = √−1. Let α and β be real numbers such that for all complex numbers z = x + iy satisfying arg⁡(z+α/z+β) = π/4, the ordered pair (x, y) lies on the circle x²+y²+5x−3y+4 = 0, Then which of the following statements is (are) TRUE?    (JEE Advanced 2021)
(a) α = −1
(b) αβ = 4
(c) αβ = −4
(d) β = 4

Ans. b and d
Circle x²+y²+5x−3y+4 = 0 cuts the real axis (X-axis) at (−4, 0), (−1, 0).

arg⁡(z+α/z+β) = π/4 implies z is on arc and (− α, 0) and (− β, 0) subtend π/4 on z.
So, α = 1 and β = 4
Hence, αβ = 1 × 4 = 4 and β = 4

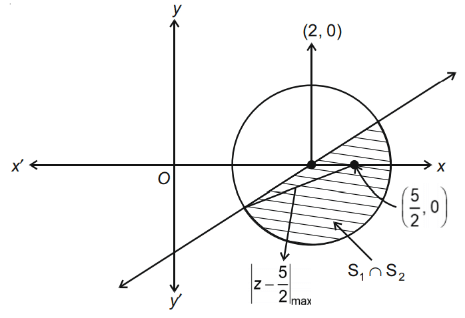
Q.32. Let C be the set of all complex numbers. Let


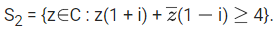
Then, the maximum value of |z−(5/2)|² for z ∈ S₁ ∩ S₂ is equal to :    (JEE Main 2021)
(a)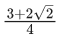
(b)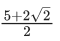
(c)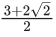
(d)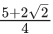

Ans. d
|t − 2| ≤ 1
Put t = x + iy

(x − 2)² + y² ≤ 1
Also, t(1 + i) +  ≥ 4
x − y ≥ 2
Let point on circle be A(2 + cosθ, sinθ)



For (AP)² maximum 

Q.33. Let n denote the number of solutions of the equation 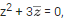 where z is a complex number. Then the value of  is equal to    (JEE Main 2021)
(a) 1
(b) 4/3
(c) 3/2
(d) 2

Ans. b
 
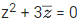
Put z = x + iy
⇒ x² − y² + 2ixy + 3(x − iy) = 0
⇒ (x² − y² + 3x) + i(2xy − 3y) = 0 + i0
∴ x² − y² + 3x = 0 ..... (1)
2xy − 3y = 0 ..... (2)
x = 3/2, y = 0
Put x = 3/2 in equation (1)



Put y = 0 ⇒ x² − 0 + 3x = 0
x = 0, −3
∴ (x, y) = (0, 0), (−3, 0)
∴ No of solutions = n = 4

Q.34. If z and ω are two complex numbers such that |zω|=1 and arg⁡(z)−arg⁡(ω)=3π/2, then 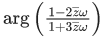 is:
(Here arg(z) denotes the principal argument of complex number z)    (JEE Main 2021)
(a) π/4
(b) -(3π/4)
(c) -(π/4)
(d) 3π/4

Ans. b
As |zω| = 1
⇒ If |z| = r, then |ω| = 1/r
Let arg⁡(z) = θ
∴ arg⁡(ω) = (θ−(3π/2))
So, z = re^iθ


Now, consider






So, option (2) is correct.

Q.35. Let a complex number be w = 1 − √3i. Let another complex number z be such that |zw| = 1 and arg(z) − arg(w) = (π/2). Then the area of the triangle with vertices origin, z and w is equal to :    (JEE Main 2021)
(a) 4
(b) 1/4
(c) 2
(d) 1/2

Ans. d

Given, w = 1 − √3 i

Also, given | zw | = 1
⇒ | z | | w | = 1 (using property)
⇒ | z | = 1/2
Also, arg(z) − arg(w) = π/2
∴ Angle between two complex number z and w is π/2.
∴ ∠zow = π/2
∴ Δzow is a right angle triangle with base ow = 2 and height oz = 1/2
∴ Area = (1/2) x 2 x (1/2) = 1/2.

Q.36. If the equation 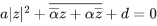 represents a circle where a, d are real constants then which of the following condition is correct?    (JEE Main 2021)
(a) |α|² − ad ≠ 0
(b) |α|² − ad > 0 and a ∈ R − {0}
(c) |α|² − ad ≥ 0 and a ∈ R
(d) α = 0, a, d ∈ R⁺

Ans. b


∴ Centre = −(α/a)


⇒ |α|² ≥ ad

Q.37. Let S₁, S₂ and S₃ be three sets defined as    (JEE Main 2021)
S₁ = {z ∈ C : |z − 1| ≤ √2}
S₂ = {z ∈ C : Re((1 − i)z) ≥ 1}
S₃ = {z ∈ C : Im(z) ≤ 1}
Then the set S₁ ∩ S₂ ∩ S₃
(a) has exactly three elements
(b) is a singleton
(c) has infinitely many elements
(d) has exactly two elements

Ans. c
Let, z = x + iy

S₁ ≡ (x − 1)² + y² ≤ 2 ..... (1)
S₂ ≡ x + y ≥ 1 ..... (2)
S₃ ≡ y ≤ 1 .... (3)
⇒ S₁ ∩ S₂ ∩ S₃ has infinitely many elements.

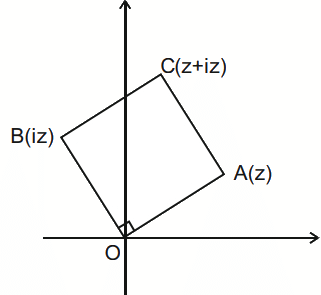
Q.38. The area of the triangle with vertices A(z), B(iz) and C(z + iz) is :    (JEE Main 2021)
(a) 1
(b) 1/2|z|²
(c) 1/2|z+iz|²
(d) 1/2

Ans. b

Each side length = |z|
Area of Δ = 1/2 (area of square)
= 1/2|z|²

Q.39. The least value of |z| where z is complex number which satisfies the inequality 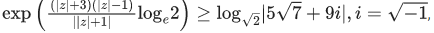 is equal to :    (JEE Main 2021)
(a) 8
(b) 3
(c) 2
(d) √5

Ans. b
Let | z | = t, t ≥ 0



t²+2t−3 ≥ 3t+3
t²− t−6 ≥ 0
t ∈ (−∞,−2)∪[3,∞) But t ≥ 0
∴ t ∈ [3,∞)

Q.40. Let a complex number z, |z| ≠ 1, satisfy 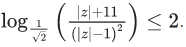 Then, the largest value of |z| is equal to ___.    (JEE Main 2021)
(a) 5
(b) 8
(c) 6
(d) 7

Ans. d

2|z|+22 ≥ (|z|−1)²
2|z|+22 ≥ |z|²−2|z|+1
|z|²−4|z|−21 ≤ 0
(|z|−7)(|z|+3) ≤ 0
⇒|z| ≤ 7
∴ |z|_max=7

Q.41. If α, β ∈ R are such that 1 − 2i (here i² = −1) is a root of z² + αz + β = 0, then (α − β) is equal to :    (JEE Main 2021)
(a) -7
(b) 7
(c) 3
(d) -3

Ans. a
1 − 2i is the root of the equation. So other root is 1 + 2i
∴ Sum of roots = 1 − 2i + 1 + 2i = 2 = -α
Product of roots = (1 − 2i)(1 + 2i) = 1 - 4i² = 5 = β
∴ α - β = -2 - 5 = -7

Q.42. Let the lines 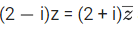 and 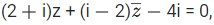 (here i² = −1) be normal to a circle C. If the line  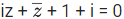is tangent to this circle C, then its radius is :    (JEE Main 2021)
(a)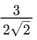
(b) 3√2
(c)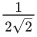  
(d) 3/√2

Ans. a

⇒ (2−i)(x+iy) = (2+i)(x−iy)
⇒ 2x−ix+2iy+y = 2x+ix−2−iy+y
⇒ 2ix−4iy = 0
L₁:x−2y = 0

⇒ (2+i)(x+iy) + (i−2)(x−iy)−4i = 0
⇒ 2x+ix+2iy−y+ix−2x+y+2iy−4i = 0
⇒ 2ix+4iy−4i = 0
L₂ : x+2y−2 = 0
Solve L₁ and L₂: x = 1, 4y = 2, y = 12
∴ x = 1
Centre (1, (1/2))

⇒ i(x+iy) + x−iy+1+i = 0
⇒ ix−y+x−iy+1+i = 0
⇒ (x−y+1) + i(x−y+1) = 0
Radius = distance from (1,(1/2)) to x−y+1=0

Q.43. Let z=a+ib,b≠0 be complex numbers satisfying 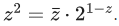 Then the least value of n ∈ N, such that zⁿ=(z+1)ⁿ, is equal to __________.    (JEE Main 2022)

Ans. 6


⇒ |z| = 21−|z|,
∵ b ≠ 0 ⇒ |z| ≠ 0
∴ |z| = 1 ...... (2)
∵ z = a+ib then
Now again from equation (1), equation (2), equation (3) we get :
a²−b² + i2ab = (a−ib)2°
∴ a²−b² = a and 2ab = −b

 then minimum value of n is 6.

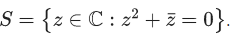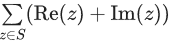Q.44. Let  Then  is equal to ____.    (JEE Main 2022)

Ans. 0

Let z = x+iy
∴ x²−y²+2ixy + x−iy = 0
(x²−y²+x) + i(2xy−y) = 0
∴ x²+y²=0 and (2x−1)y = 0
if x = +(1/2) then y = ±(√3/2)
And if y = 0 then x = 0,−1
∴
∴ ∑(R_e(z) + m(z)) = 0

Q.45. Let S = {z ∈ C : |z − 3| ≤ 1 and z(4 + 3i) + 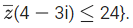  If α + iβ is the point in S which is closest to 4i, then 25(α + β) is equal to ___________.    (JEE Main 2022)

Ans. 80
Here |z−3|<1
⇒ (x−3)²+y²<1
and z = (4+3i)+≤24
⇒ 4x−3y ≤ 12
tan⁡θ = 4/3

∴ Coordinate of P = (3−cos⁡θ, sin⁡θ)


∴ 25(α + β) = 80

Q.46. If z²+z+1 = 0, z ∈ C, then  is equal to _________.    (JEE Main 2022)

Ans. 2
∵ z/+z+1 = 0
⇒ ω or ω²


= |0 + 0 - 2|
= 2

Q.47. The number of elements in the set {z = a + ib ∈ C : a, b ∈ Z and 1 < | z − 3 + 2i | < 4} is __________.    (JEE Main 2022)

Ans. 40

Q.48. Sum of squares of modulus of all the complex numbers z satisfying 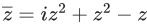 is equal to _____.    (JEE Main 2022)

Ans. 2

Q.49. Let S = {z ∈ C:|z−2| ≤ 1, z(1+i)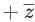(1−i) ≤ 2}. Let |z−4i| attains minimum and maximum values, respectively, at z₁ ∈ S and z₂ ∈ S. If 5(|z₁|²+|z₂|²) = α+β√5, where α and β are integers, then the value of α + β is equal to ___________.    (JEE Main 2022)

Ans. 26

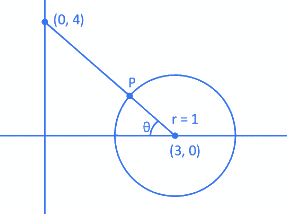
Q.50. If for the complex numbers z satisfying | z − 2 − 2i | ≤ 1, the maximum value of | 3iz + 6 | is attained at a + ib, then a + b is equal to ______________.    (JEE Main 2021)

Ans. 5
|z − 2 − 2i| ≤ 1
|x + iy − 2 − 2i| ≤ 1
|(x − 2) + i(y − 2)| ≤ 1
(x − 2)2 + (y − 2)2 ≤ 1
| 3iz + 6 |_max at a + ib
|3i||z + (6/3i)|
3|z−2i|_max

From figure maximum distance at 3 + 2i
a + ib = 3 + 2i = a + b = 3 + 2 = 5 Ans.

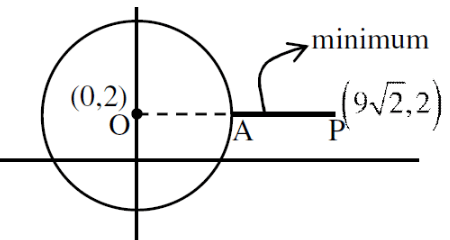
Q.51. A point z moves in the complex plane such that 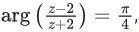 then the minimum value of |z - 9√2 - 2i|² is equal to ___.      (JEE Main 2021)

Ans. 98
Let z = x+iy

arg⁡(x−2+iy) − arg⁡(x+2+iy) = π/4


4y = x²−4+y²
x²+y²−4y−4 = 0
locus is a circle with center (0, 2) & radius = 2√2

min. value = (AP)² = (OP−OA)²
= (9√2−2√2)²
= (7√2)² = 98

Q.52. The least positive integer n such that 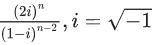 is a positive integer, is ____.     (JEE Main 2021)

Ans. 6


This is positive integer for n = 6

Q.53. Let  Then the value of 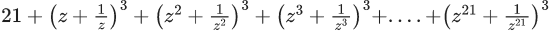 is  ____.     (JEE Main 2021)

Ans. 13

= 21 − 2 − 6
= 13

Q.54. The equation of a circle is Re(z²) + 2(Im(z))² + 2Re(z) = 0, where z = x + iy. A line which passes through the center of the given circle and the vertex of the parabola, x² − 6x − y + 13 = 0, has y-intercept equal to  ______.     (JEE Main 2021)

Ans. 1
Equation of circle is (x² − y²) + 2y² + 2x = 0
x² + y² + 2x = 0
Centre : (−1, 0)
Parabola : x² − 6x − y + 13 = 0
(x − 3)² = y − 4
Vertex : (3, 4)
Equation of line ≡ y−0 = ((4−0)/(3+1))(x+1)
y = x+1
y-intercept = 1

Q.55. If the real part of the complex number  is zero, then the value of sin²3θ + cos²θ is equal to _______.    (JEE Main 2021)

Ans. 1

⇒ θ = π/4
Hence, sin²3θ + cos²θ = 1.

Q.56. Let 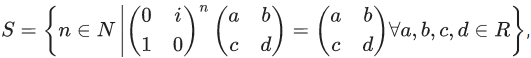 where i = √−1. Then the number of 2-digit numbers in the set S is ______.    (JEE Main 2021)

Ans. 11
Let
⇒ AX = IX
⇒ A = I


⇒ n is multiple of 8
So, number of 2 digit numbers in the set
S = 11 (16, 24, 32, .........., 96)

Q.57. Let z₁, z₂ be the roots of the equation z² + az + 12 = 0 and z₁, z₂ form an equilateral triangle with origin. Then, the value of |a| is    (JEE Main 2021)

Ans. 6
For equilateral triangle with vertices z₁, z₂ and z₃,

Here one vertex z₃ is 0

Given, z₁, z₂ are roots of z²+az+12 = 0
∴ z₁+z₂ = −a
z₁z₂ = 12

⇒ (z₁+z₂)² = 3z₁z₂
⇒ (−a)² = 3×12
⇒ a² = 36
⇒ a = ±6
⇒ |a| = 6

Q.58. Let z and ω be two complex numbers such that 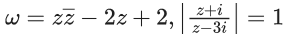 and Re(ω) has minimum value. Then, the minimum value of n ∈ N for which ωⁿ is real, is equal to ____.     (JEE Main 2021)

Ans. 4
Let z = x + iy
| z + i | = | z − 3i |
⇒ y = 1
Now
ω = x² + y² − 2x − 2iy + 2
ω = x² + 1 − 2x − 2i + 2
Re(ω) = x² − 2x + 3
Re(ω) = (x − 1)² + 2
Re(ω)_min at x = 1 ⇒ z = 1 + i
Now,
ω = 1 + 1 − 2 − 2i + 2
ω = 2(1 − i) = 2√2eⁱ((−π)/4)
ωⁿ = 2√2eⁱ((−nπ)/4)
If ωⁿ is real ⇒ n = 4

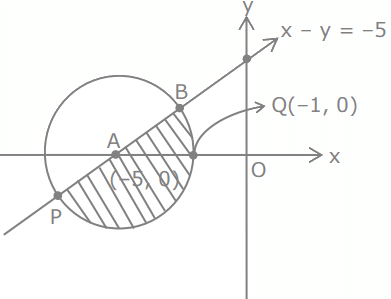
Q.59. Let z be those complex numbers which satisfy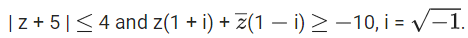
If the maximum value of |z + 1|² is α + β√2, then the value of (α + β) is ____________.     (JEE Main 2021)

Ans. 48
Let, z = x + iy


⇒ 2x + i (2iy) ≥ − 10
⇒ x + i2 y ≥ − 5
⇒ x − y ≥ − 5 ...... (1)
Also given, | z + 5 | ≤ 4
⇒ | z − (−5 + 0i) | ≤ 4 ...... (2)
It represents a circle whose center at (− 5, 0) and radius 4. z is inside of the circle.

From (1) and (2) z is the shaded region of the diagram.
Now, | z + 1 | = | z − (−1 + 0 i) | = distance of z from (−1, 0).
Clearly 'p' is the required position of 'z' when | z + 1 | is maximum.
∴ P ≡ (−5 − 4 cos45∘, 0 − 4sin45∘) = (−5−2√2, −2√2)
∴ (PQ)²|_max = 32 + 16√2
⇒ α = 32
⇒ β = 16
Thus, α + β = 48

Q.60. Let 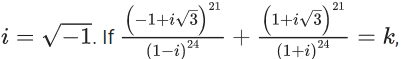 and n = [|k|] be the greatest integral part of |k|. Then  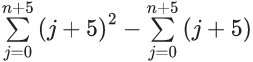is equal to _____.      (JEE Main 2021)

Ans. 310
(1+i)² = 1+i²+2i = 1−1+2i = 2i
(1−i)² = 1+i²−2i = 1−1−2i = −2i
We know,





Now,




Now




= 55 + 135 + 120
= 310

Q.61. If the least and the largest real values of a, for which the equation z + α|z – 1| + 2i = 0 (z ∈ C and i = √−1) has a solution, are p and q respectively; then 4(p² + q²) is equal to ______.    (JEE Main 2021)

Ans. 10


y = −2 & x² = α²(x²−2x+1+4)

x ∈ R ⇒ D ≥ 0
4α⁴ − 4(α² − 1)5α² ≥ 0
α²[4α² − 2α² + 20] ≥ 0
α²[−16α² + 20] ≥ 0
α²[α² − (5/4)] ≤ 0



then