JEE Main Previous Year Questions (2021-23): Inverse Trigonometric Functions PDF Download

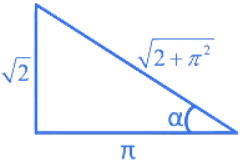
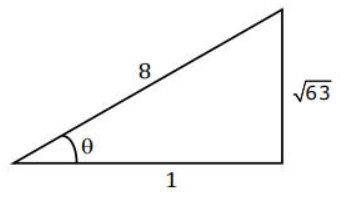
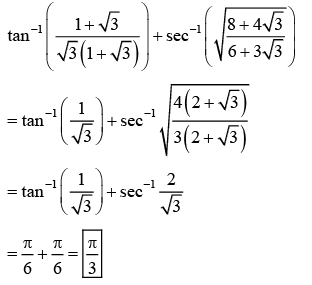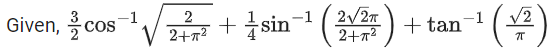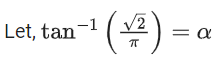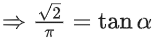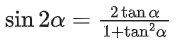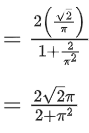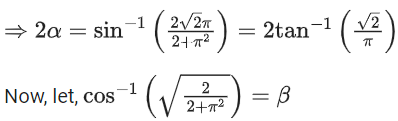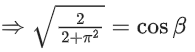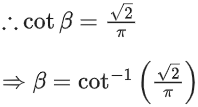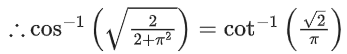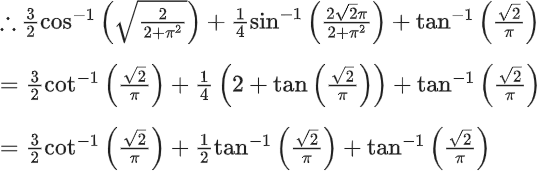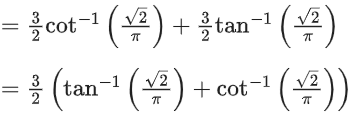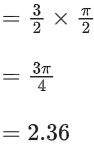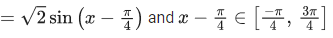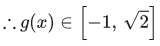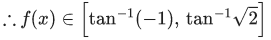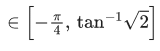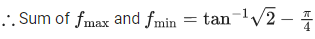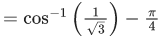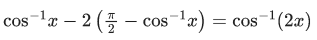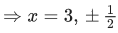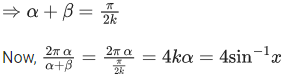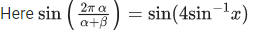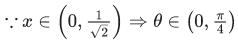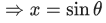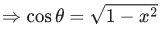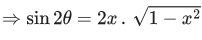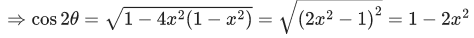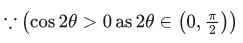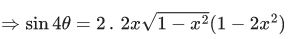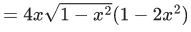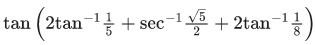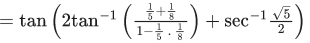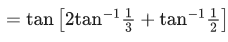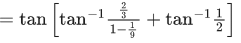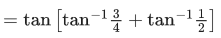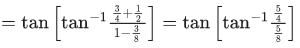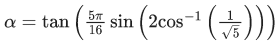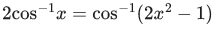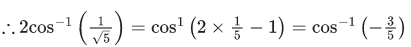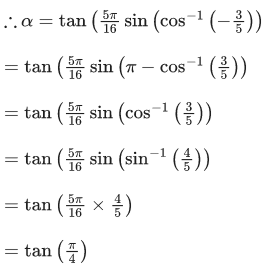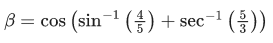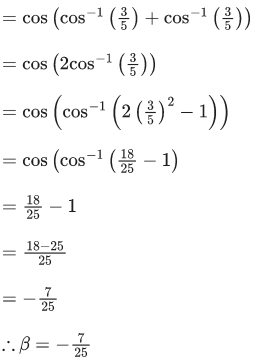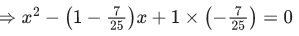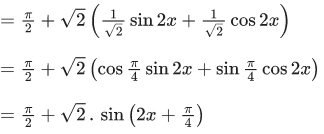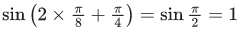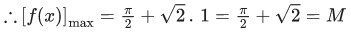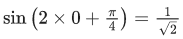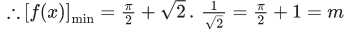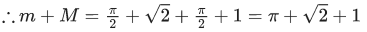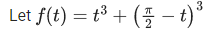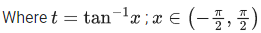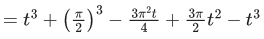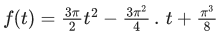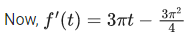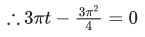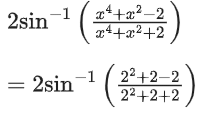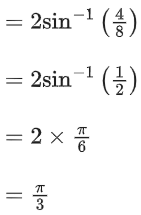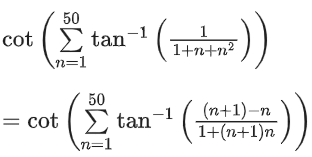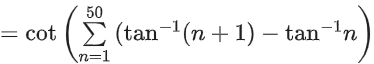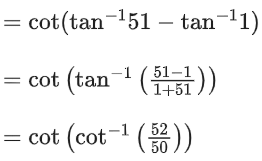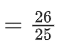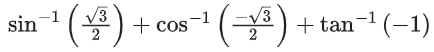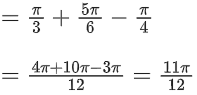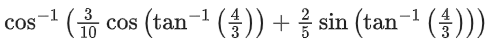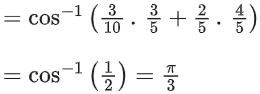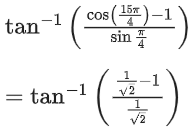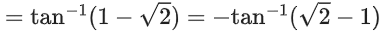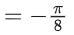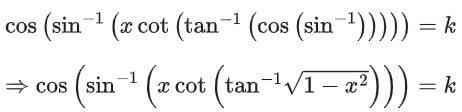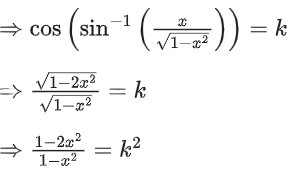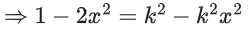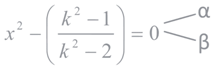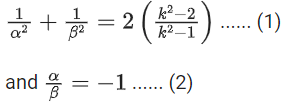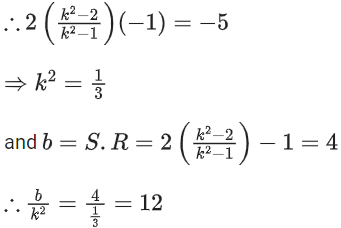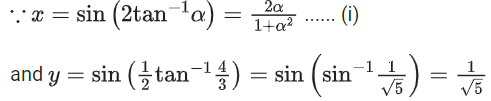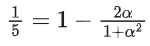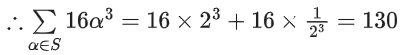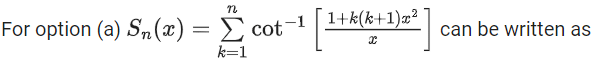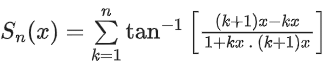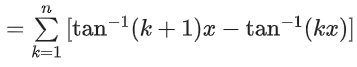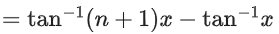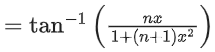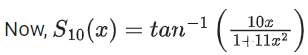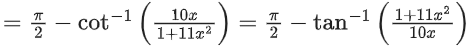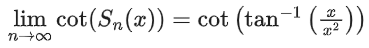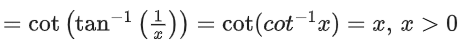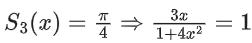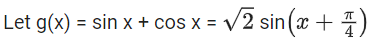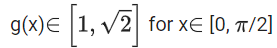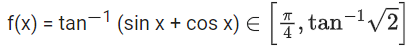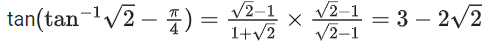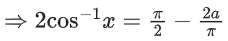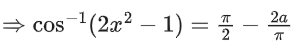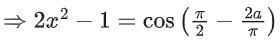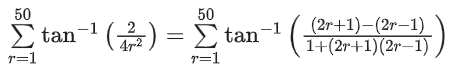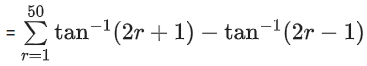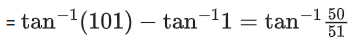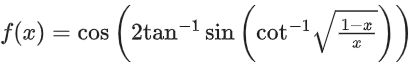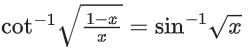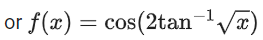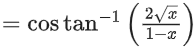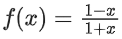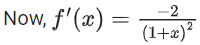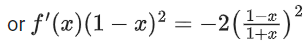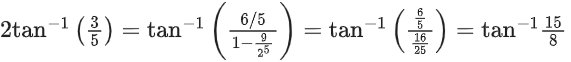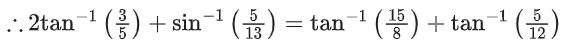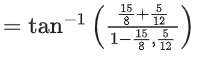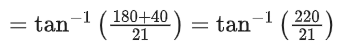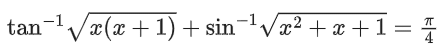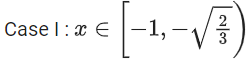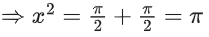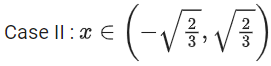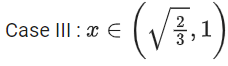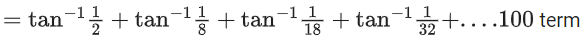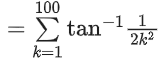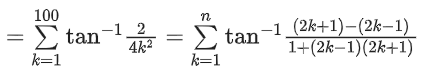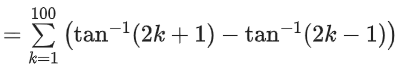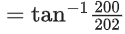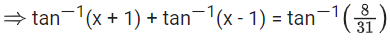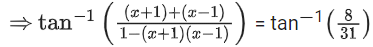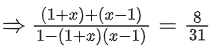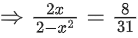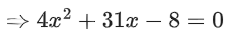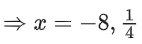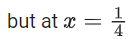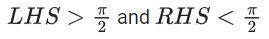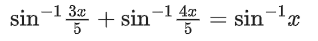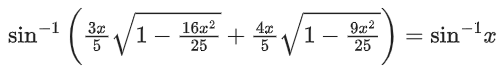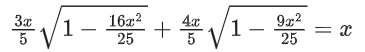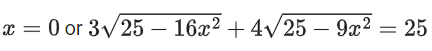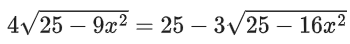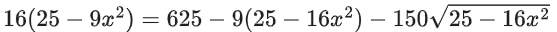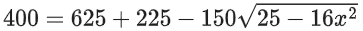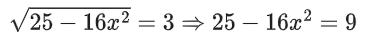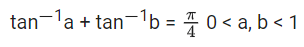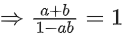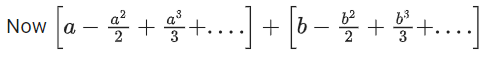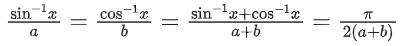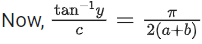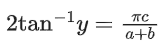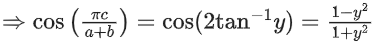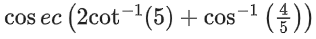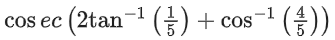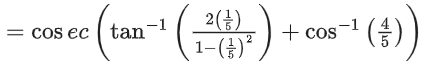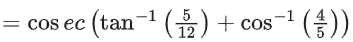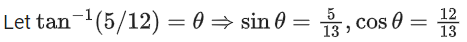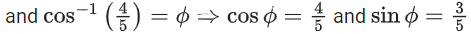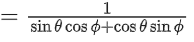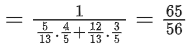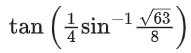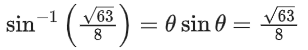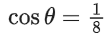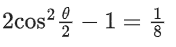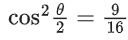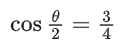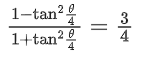Q.1. 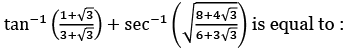           (JEE Main 2023)
(a) π/3
(b) π/4
(c) π/6
(d) π/2

Ans. a

Q.2. Considering only the principal values of the inverse trigonometric functions, the value of 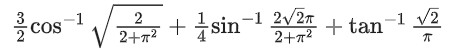is      (JEE Advanced 2022) 

Ans. Between 2.35 and 2.37




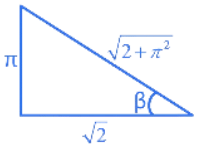
We know,

Q.3. The sum of the absolute maximum and absolute minimum values of the function f(x) = tan^−1⁡ (sin ⁡x − cos ⁡x) in the interval [0, π] is:      (JEE Main 2022)
(a) 0
(b)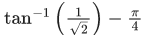
(c)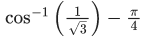
(d) -π/12

Ans. c
f(x) = tan⁻¹(sin ⁡x − cos ⁡x), [0, π]
Let g(x)  = sin x - cos x


and tan⁻¹x is an increasing function

Q.4. Considering the principal values of the inverse trigonometric functions, the sum of all the solutions of the equation cos⁻¹⁡(x) − 2sin⁻¹⁡(x) = cos⁻¹⁡(2x) is equal to:      (JEE Main 2022)
(a) 0
(b) 1
(c) 12
(d)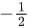

Ans. a
cos⁻¹x − 2sin⁻¹ x = cos⁻¹2x
For Domain : x ∈ [−1/2, 1/2]

⇒ cos⁻¹x + 2 cos⁻¹x = π + cos⁻¹2x
⇒ cos⁡ (3 cos⁻¹x) = −cos⁡(cos⁻¹2x)
⇒ 4x³ = x

Q.5. 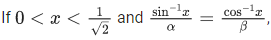  then the value of  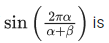     (JEE Main 2022)
(a)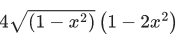
(b)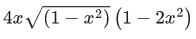
(c)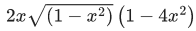
(d)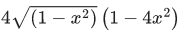

Ans. b



Let sin⁻¹x = θ

Q.6. 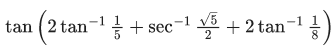 is equal to:      (JEE Main 2022)
(a) 1
(b) 2
(c) 1/4
(d) 5/4

Ans. b






= tam[tan ^-12] = 2

Q.7. Let α = tan⁡(5π/16 sin ⁡(2cos⁻¹(1/√5))) and β = cos⁡(sin⁻¹(4/5) + sec⁻¹(5/3)) where the inverse trigonometric functions take principal values. Then, the equation whose roots are α and β is:      (JEE Main 2022)
(a) 15x² − 8x − 7 = 0
(b) 5x² − 12x + 7 = 0
(c) 25x² − 18x − 7 = 0
(d) 25x² − 32x + 7 = 0

Ans. c
Given,

We know,



= 1
∴ α = 1
Also given,


∴ The quadratic equation with roots α and β is
x² − (α + β)x + αβ = 0

⇒ 25x² − 18x − 7 = 0

Q.8. Let m and M respectively be the minimum and the maximum values of f(x) = sin⁻¹2x + sin⁡ 2x + cos⁻¹2x + cos ⁡2x, x ∈ [0, π/8]. Then m + M is equal to:      (JEE Main 2022)
(a) 1 + 2 + π
(b) (1 +2 )π
(c) π + 2
(d) 1 + π

Ans. a
f(x) = sin⁻¹(2x) + sin ⁡2x + cos⁻¹(2x) + cos⁡ 2x
= sin⁻¹(2x) + cos⁻¹(2x) + sin⁡ 2x + cos ⁡2x

f(x) is maximum when  is maximum means x = π/8 or


f(x) is minimum when sin   is minimum means x = 0 or

Q.9. The set of all values of k for which (tan⁻¹x)³ + (cot⁻¹x)³ = kπ³, x ∈ R, is the interval:      (JEE Main 2022)
(a)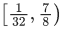
(b)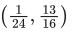
(c)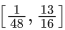
(d)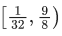

Ans. a
(tan⁻¹x)³ + (cot⁻¹x)³ = kπ³




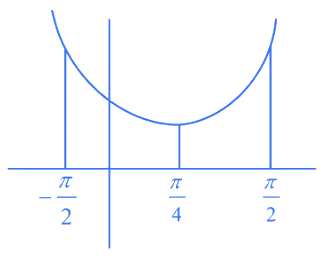
This is a quadratic equation of t.
Here, coefficient of t² term is 3π/2 which is > 0.
∴ It is a upward parabola.

f″(t) = 3π > 0

⇒ t = π/4 (minima)
∴ vertex of graph at  π/4

Q.10. Let x ∗ y = x² + y³ and (x ∗ 1) ∗ 1 = x ∗ (1 ∗ 1).

Then a value of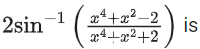        (JEE Main 2022)
(a) π/4 
(b) π/3 
(c) π/2 
(d) π/6

Ans. b
Given,

x ∗ y = x² + y³

∴ x ∗ 1 = x² + 1³ = x² + 1

Now, (x ∗ 1) ∗ 1 = (x² + 1) ∗ 1

⇒ (x ∗ 1) ∗ 1 = (x² + 1)² + 1³

⇒ (x ∗ 1) ∗ 1 = x⁴ + 1 + 2x² + 1

Also, x ∗ (1 ∗ 1)

= x ∗ (1² + 1³)

= x ∗ 2

= x² + 2³

= x² + 8

Given that,

(x ∗ 1) ∗ 1 = x ∗ (1 ∗ 1)

∴ x⁴ + 1 + 2x² + 1 = x² + 8

⇒ x⁴ + x² − 6 = 0

⇒ x⁴ + 3x² − 2x² − 6 = 0

⇒ x²(x² + 3) − 2(x³ + 3) = 0

⇒ (x² + 3)(x² − 2) = 0

⇒ x² = 2, −3

[x² = −3 not possible as square of anything should be always possible]

∴ x² = 2

∴ Now,

Q.11. The value of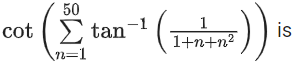        (JEE Main 2022)
(a) 26/25
(b) 25/26
(c) 50/51
(d) 52/51

Ans. a

Q.12.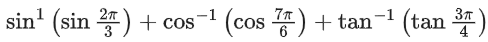is equal to:      (JEE Main 2022)
(a) 11π/12
(b) 17π/12
(c) 31π/12
(d)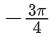

Ans. a

Q.13. If the inverse trigonometric functions take principal values then

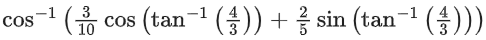is equal to:      (JEE Main 2022)
(a) 0
(b) π/4
(c) π/3
(d) π/6

Ans. c

Q.14. The value of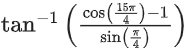is equal to:      (JEE Main 2022)
(a)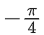
(b)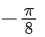
(c)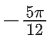
(d)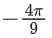

Ans. b

Q.15. For k ∈ R, let the solutions of the equation cos⁡(sin⁻¹⁡(xcot⁡(tan⁻¹⁡(cos⁡(sin^−1⁡x))))) = k,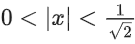be α and β, where the inverse trigonometric functions take only principal values. If the solutions of the equation x² − bx − 5 = 0 are 1/α² + 1/β² and α/β, then b/k² is equal to ____________.       (JEE Main 2022)

Ans. 12



∴

Q.16. Let x = sin⁡(2tan⁻¹α) and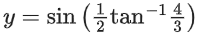. If S = {a ∈ R : y² = 1−x}, then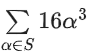is equal to _______________.       (JEE Main 2022)

Ans. 130

Now, y² = 1 − x

⇒ 1 + α² = 5 + 5α² − 10α
⇒ 2α² − 5α + 2 = 0
∴ α = 2, 1/2

Q.17. 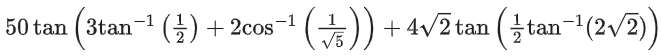is equal to ____________.       (JEE Main 2022)

Ans. 29

Q.18. For any positive integer n, let S_n : (0, ∞) → R be defined by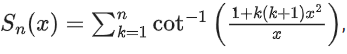where for any x ∈ R, cot⁻¹(x) ∈ (0, π) and tan⁻¹(x) ∈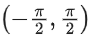. Then which of the following statements is (are) TRUE?        (JEE Advanced 2021) 
(a)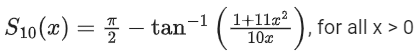
(b)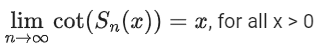
(c)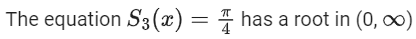
(d)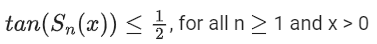

Ans. a, b







Option (a) is correct.
For option (b)


Option (b) is correct.
For option (c) 

⇒ 4x² − 3x + 1 = 0 has no real root.
Option (c) is incorrect.
For option (d) 
which is greater than 1/2 for n ≥ 3
Option (d) is incorrect.

Q.19. cos⁻¹(cos⁡(−5)) + sin⁻¹(sin⁡(6)) − tan⁻¹(tan⁡(12)) is equal to:       (JEE Main 2021)
(The inverse trigonometric functions take the principal values)
(a) 3π − 11
(b) 4π − 9
(c) 4π − 11
(d) 3π + 1

Ans. c
cos⁻¹(cos⁡(−5)) + sin⁻¹(sin⁡(6)) − tan⁻¹(tan⁡(12))
= (2π − 5) + (6 − 2π) − (12 − 4π)
= 4π − 11.

Q.20. Let M and m respectively be the maximum and minimum values of the function f(x) = tan⁻¹ (sin x + cos x) in [0, π/2], then the value of tan(M − m) is equal to:       (JEE Main 2021)
(a) 2 + √3
(b) 2 − √3
(c) 3 + 2√2
(d) 3 − 2√2

Ans. d

Q.21. If (sin⁻¹x)² − (cos⁻¹x)² = a; 0 < x < 1, a ≠ 0, then the value of 2x² − 1 is:       (JEE Main 2021)
(a) cos⁡(4a/π)
(b) sin⁡(2a/π)
(c) cos⁡(2a/π)
(d) sin⁡(4a/π)

Ans. b
Given a = sin⁻¹x)² − (cos⁻¹x)²
= (sin⁻¹x + cos⁻¹x)(sin⁻¹x − cos⁻¹x)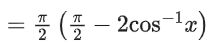
 

Q.22.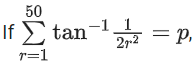then the value of tan p is:       (JEE Main 2021)
(a) 101/102
(b) 50/51
(c) 100
(d) 51/50

Ans. b

Q.23. Let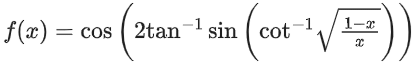0 < x < 1. Then:       (JEE Main 2021)
(a) (1 − x)²f′(x) − 2(f(x))² = 0
(b) (1 + x)²f′(x) + 2(f(x))² = 0
(c) (1 − x)²f′(x) + 2(f(x))² = 0
(d) (1 + x)²f′(x) − 2(f(x))² = 0

Ans. c







or (1 − x)²f′(x) + 2(f(x))² = 0

Q.24. The value of tan⁡(2tan⁻¹(3/5) + sin⁻¹(5/13)) is equal to:       (JEE Main 2021)
(a) −181/69
(b) 220/21
(c) −291/76
(d) 151/63

Ans. b

Q.25. The number of real roots of the equation 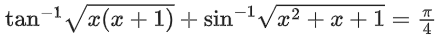 is:       (JEE Main 2021)
(a)1
(b) 2
(c) 4
(d) 0

Ans. d

For equation to be defined,
x² + x ≥ 0
⇒ x² + x + 1 ≥ 1
∴ Only possibility that the equation is defined
x² + x = 0 ⇒ x = 0; x = −1
None of these values satisfy
∴ No of roots = 0 

Q.26. The number of solutions of the equation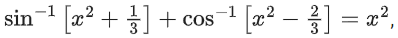for x ∈ [−1, 1], and [x] denotes the greatest integer less than or equal to x, is:       (JEE Main 2021)
(a) 0
(b) Infinite
(c) 2
(d) 4

Ans. a
There are three cases possible for x ∈ [−1, 1]

∴ sin⁻¹(1) + cos⁻¹(0) = x²

⇒ x = ±√π → (Reject)

∴ sin⁻¹(0) + cos⁻¹(−1) = x²
⇒ 0 + π = x²
⇒ x = ±√x → (Reject)

∴ sin⁻¹(0) + cos⁻¹(0) = x²
⇒ x² − π ⇒ x − ±√x (Reject)
∴ No solution. There, the correct answer is (a).

Q.27. If cot⁻¹(α) = cot⁻¹ 2 + cot⁻¹ 8 + cot⁻¹ 18 + cot⁻¹ 32 + ...... upto 100 terms, then α is:       (JEE Main 2021) 
(a) 1.02
(b) 1.03
(c) 1.01
(d) 1.00

Ans. c
cot⁻¹(α) = cot⁻¹2 + cot⁻¹8 + cot⁻¹18 + cot⁻¹32 +....100 terms




= tan⁻¹201 − tan⁻¹1

= cot⁻¹(1.01)
Hence α = 1.01

Q.28. The sum of possible values of x for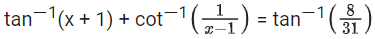
is:       (JEE Main 2021) 
(a)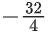
(b)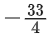
(c)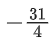
(d)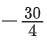

Ans. a









So, only solution is x = − 8 =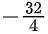 

Q.29. Given that the inverse trigonometric functions take principal values only. Then, the number of real values of x which satisfy sin⁻¹(3x/5) + sin⁻¹(4x/5) = sin⁻¹x is equal to:       (JEE Main 2021) 
(a) 2
(b) 0
(c) 3
(d) 1

Ans. c





Squaring we get



⇒ x² = 1
Put x = 0, 1, −1 in the original equation
We see that all values satisfy the original equation.
Number of solution = 3 

Q.30. If 0 < a, b < 1, and tan⁻¹a + tan⁻¹b = π/4, then the value of 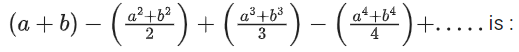       (JEE Main 2021) 
(a) log_e2
(b) e
(c) log_e(e/2)
(d) e² = 1

Ans. a


a + b = 1 − ab
(a + 1)(b + 1) = 2

= log_e(1 + a) + log_e(1 + b)
(∵ expansion of loge(1 + x))
= log_e[(1 + a)(1 + b)]
= log_e2

Q.31. If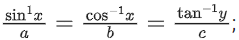0 < x < 1, then the value of 

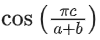is:       (JEE Main 2021) 
(a)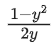
(b)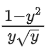
(c) 1 - y²
(d)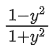

Ans. d

Q.32. cosec[2cot⁻¹(5) + cos⁻¹(4/5)] is equal to:        (JEE Main 2021) 
(a) 75/56
(b) 65/56
(c) 56/33
(d) 65/33

Ans. b






= cos⁡ec(θ + ϕ)

Q.33. A possible value of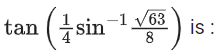        (JEE Main 2021) 
(a) √7 − 1
(b) 1/√7
(c) 2√2 − 1
(d)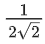

Ans. b