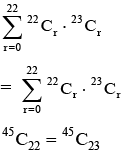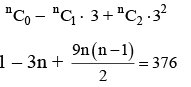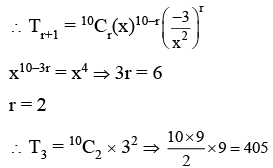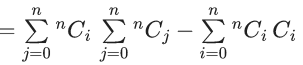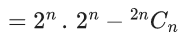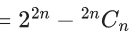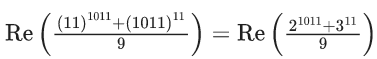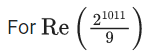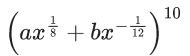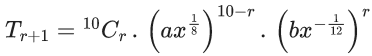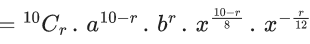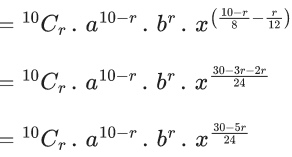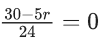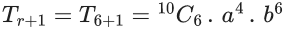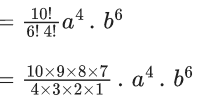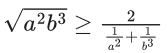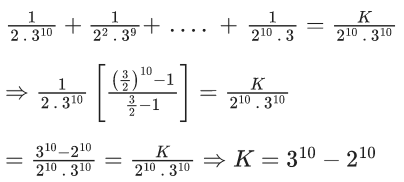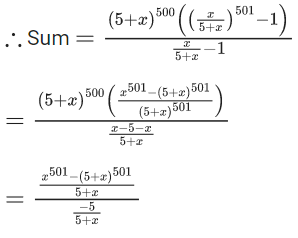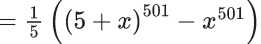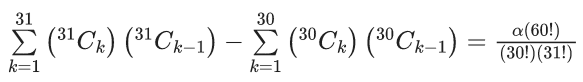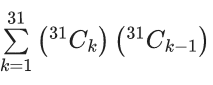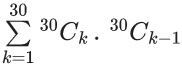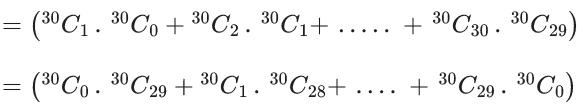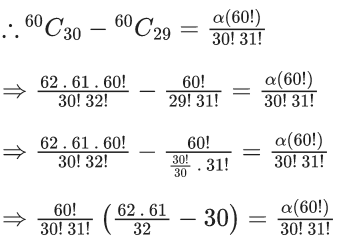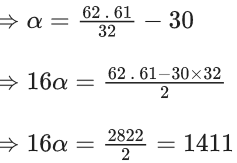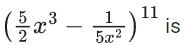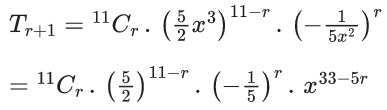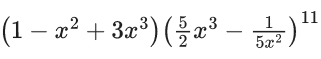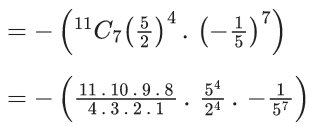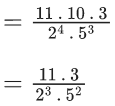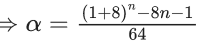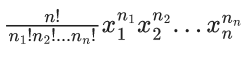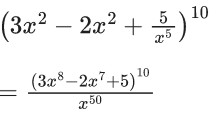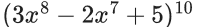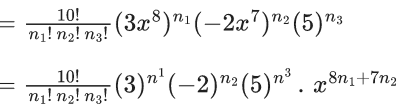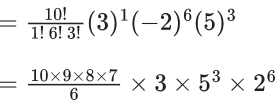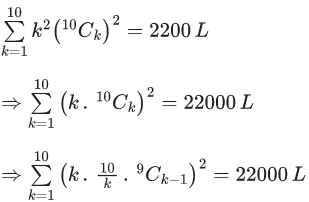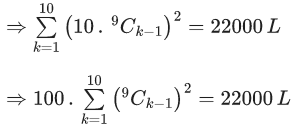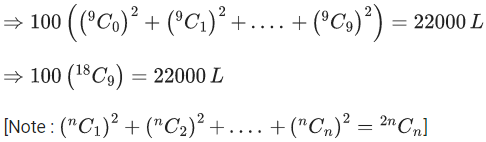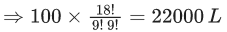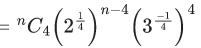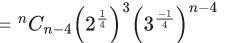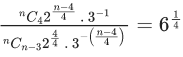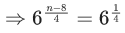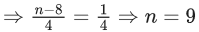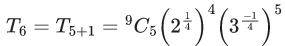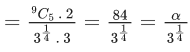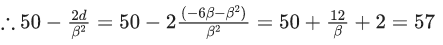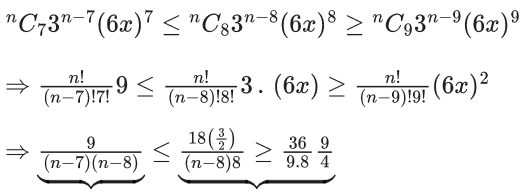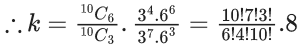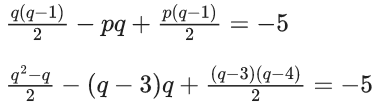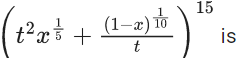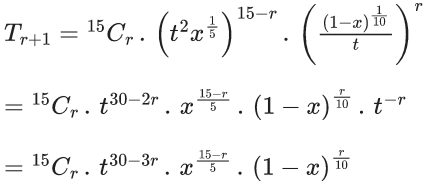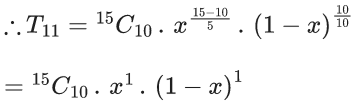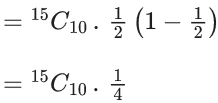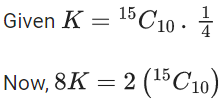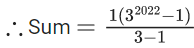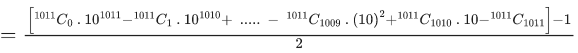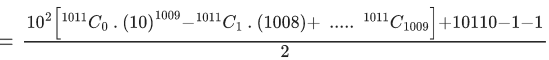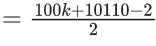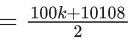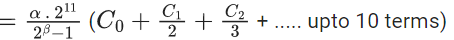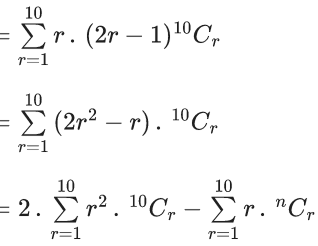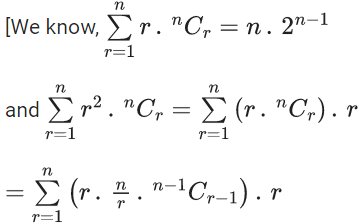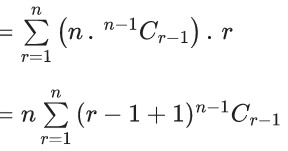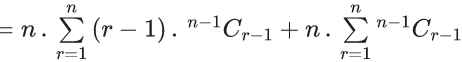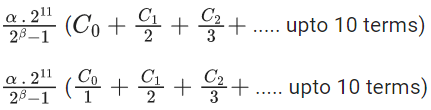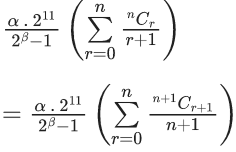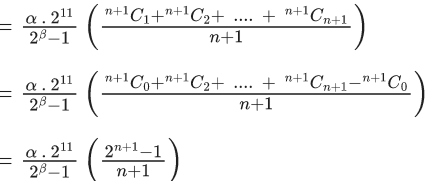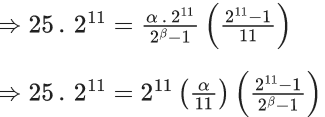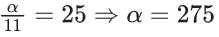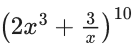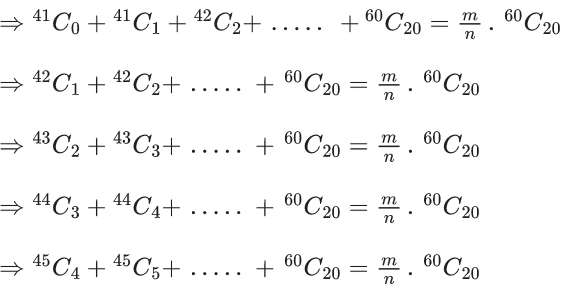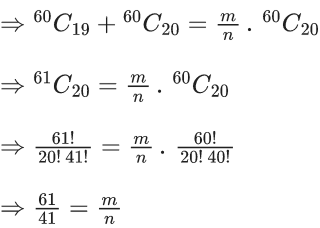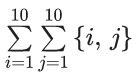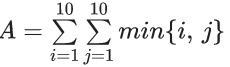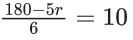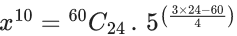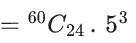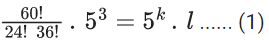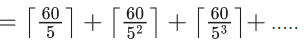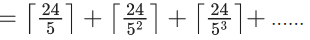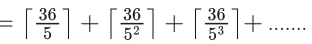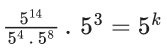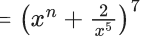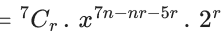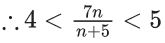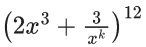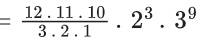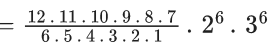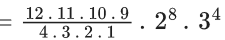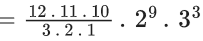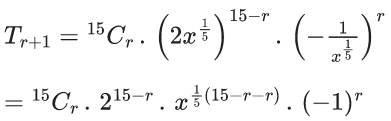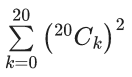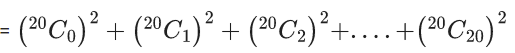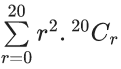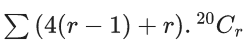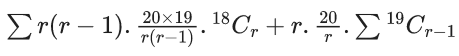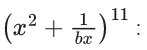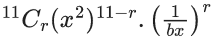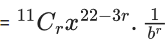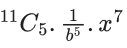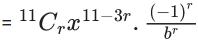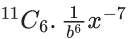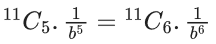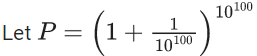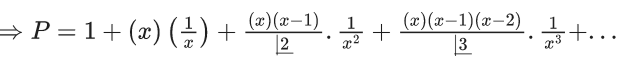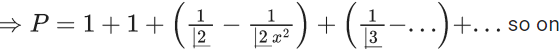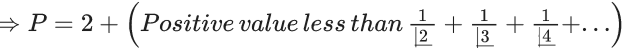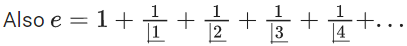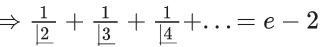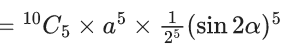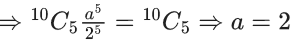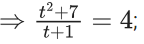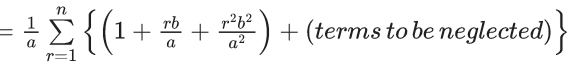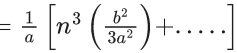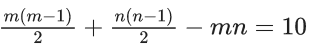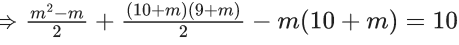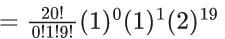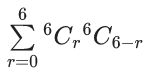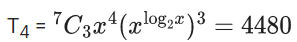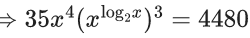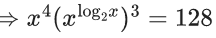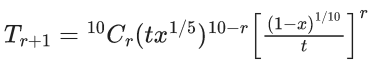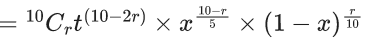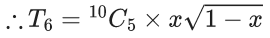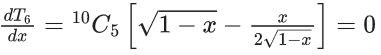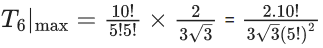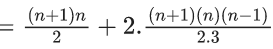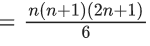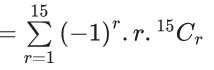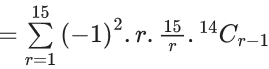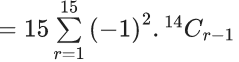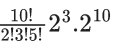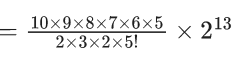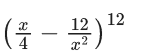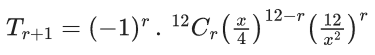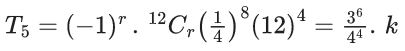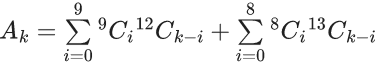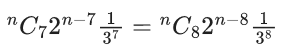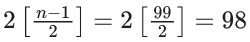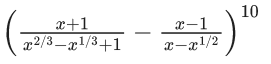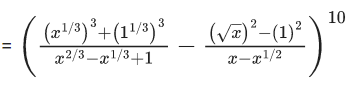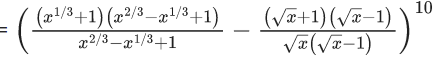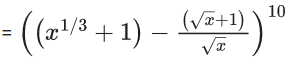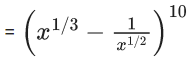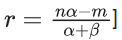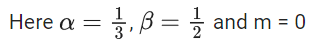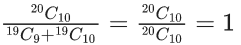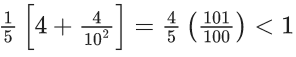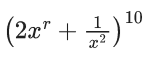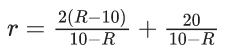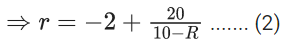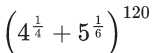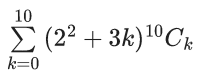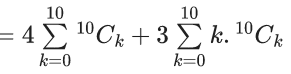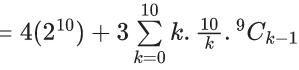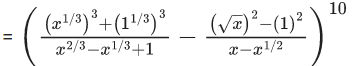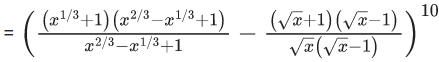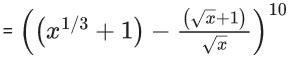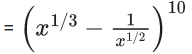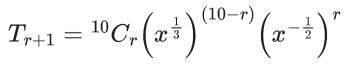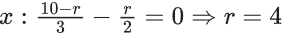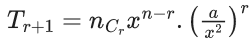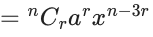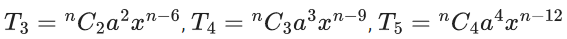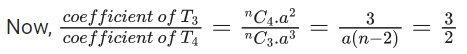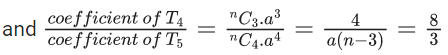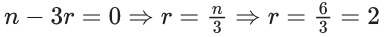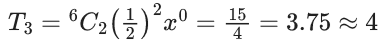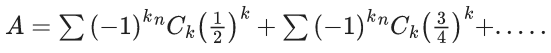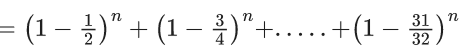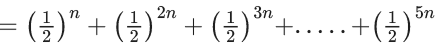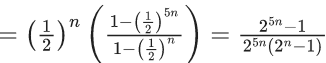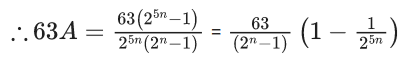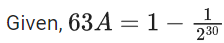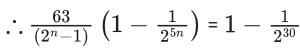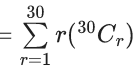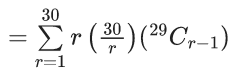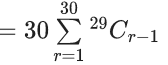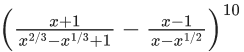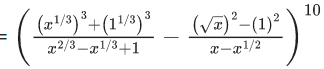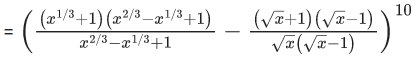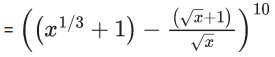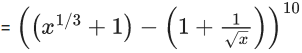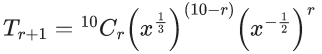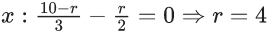JEE Main Previous year questions (2021-23): Mathematical Induction and Binomial Theorem PDF Download

Q.1. The value of 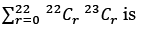       (JEE Main 2023)
(a) ⁡⁴⁴C₂₃ 
(b) ⁡⁴⁵C₂₃
(c) ⁡⁴⁴C₂₂ 
(d) ⁡⁴⁵C₂₄   

Ans. b

Q.2. Let the sum of the coefficients of the first three terms in the expansion of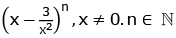 , be 376. Then the coefficient of x⁴ is      (JEE Main 2023)

Ans. 405

2 – 6n + 9n² – 9n = 752
9n² – 15n – 750 = 0
3n² – 5n – 250 = 0
3n² – 30n + 25n – 250 = 0
(3n + 25) (n – 10) = 0
n = 10

 
Q.3. The remainder when 7²⁰²² + 3²⁰²² is divided by 5 is :     (JEE Main 2022)
(a) 0
(b) 2
(c) 3
(d) 4

Ans. c
Let E = 7²⁰²² + 3²⁰²²
= (15−1)¹⁰¹¹ + (10−1)¹⁰¹¹
= −1 + (multiple of 15) −1 + multiple of 10
= −2 + (multiple of 5)
Hence remainder on dividing E by 5 is 3.

Q.4. The remainder when (2021)²⁰²² + (2022)²⁰²¹ is divided by 7 is     (JEE Main 2022)
(a) 0
(b) 1
(c) 2
(d) 6

Ans. a
(2021)²⁰²²+(2022)²⁰²¹
= (7k−2)²⁰²² + (7k1−1)²⁰²¹
= [(7k−2)³]⁶⁷⁴ + (7k₁₎²⁰²¹ − 2021(7k₁)²⁰²⁰ +.... −1
= (7k₂−1)⁶⁷⁴ + (7m−1)
= (7n+1) + (7m−1) = 7(m+n) (multiple of 7)
∴ Remainder = 0

Q.5. 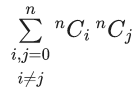 is equal to    (JEE Main 2022)
(a) 2²ⁿ − ²ⁿC_n
(b) 2^{2n − 1}−²ⁿ⁻¹C_n−1
(c) 2²ⁿ − (1/2)²ⁿC_n
(d) 2²ⁿ⁻¹ + ²ⁿ⁻¹C_n

Ans. b

Q.6. The remainder when (11)¹⁰¹¹ + (1011)¹¹ is divided by 9 is     (JEE Main 2022)
(a) 1
(b) 4
(c) 6
(d) 8

Ans. d

2¹⁰¹¹=(9 − 1)³³⁷ = ³³⁷C₀9³³⁷(−1)⁰ + ³³⁷C₁9³³⁶(−1)¹ + ³³⁷C₂9³³⁵(−1)² +.....+ ³³⁷C₃₃₇9⁰(−1)³³⁷
So, remainder is 8
and Re(3¹¹/9)=0
So, remainder is 8.

Q.7. For two positive real numbers a and b such that 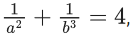 then minimum value of the constant term in the expansion of  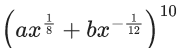is :     (JEE Main 2022)
(a) 105/2
(b) 105/4
(c) 105/8
(d) 105/16

Ans. c
Given, Binomial expansion,
General term,



For constant term, 

⇒ r = 6
∴ Constant term,


= 210a⁴b⁶
We know, GM ≥ HM
For terms a² and b³,


∴ Minimum value of a⁴b⁶ = 1/16
∴ Minimum value of constant term
T₇ = 210 × a⁴b⁶
= 210 × (1/16)
= 105/8

Q.8. The remainder when 3²⁰²² is divided by 5 is :     (JEE Main 2022)
(a) 1
(b) 2
(c) 3
(d) 4

Ans. d
3²⁰²²
= (3²)¹⁰¹¹
= (9)¹⁰¹¹
= (10−1)¹⁰¹¹
= ¹⁰¹¹C₀(10)¹⁰¹¹ +.....+ ¹⁰¹¹C₁₀₁₀.(10)¹ − ¹⁰¹¹C₁₀₁₁
= 10[¹⁰¹¹C₀(10)¹⁰¹⁰ +......+ ¹⁰¹¹C₁₀₁₀]−1
= 10K−1
[As 10[¹⁰¹¹C₀.(10)¹⁰¹⁰ +......+ ¹⁰¹¹C₁₀₁₀] is multiple of 10]
= 10K + 5 − 5 − 1
= 10K − 5 + 5 − 1
= 5(2K − 1) + 4
∴ Unit digit = 4 when divided by 5.

Q.9. If  then the remainder when K is divided by 6 is :     (JEE Main 2022)
(a) 1
(b) 2
(c) 3
(d) 5

Ans. d

Now K = (1+2)¹⁰ − 2¹⁰
= ¹⁰C₀ + ¹⁰C₁2 + ¹⁰C₂2³ +....+ ¹⁰C₁₀2¹⁰ − 2¹⁰
= ¹⁰C₀ + ¹⁰C₁2 + 6λ + ¹⁰C₉.2⁹
= 1+20+5120+6λ
= 5136+6λ+5
= 6μ+5
λ, μ ∈ N
∴ remainder = 5

Q.10. The coefficient of x¹⁰¹ in the expression (5+x)⁵⁰⁰ + x(5+x)⁴⁹⁹ + x²(5+x)⁴⁹⁸ +.....+ x⁵⁰⁰, x > 0, is     (JEE Main 2022)
(a) ⁵⁰¹C₁₀₁ (5)³⁹⁹
(b) ⁵⁰¹C₁₀₁ (5)⁴⁰⁰
(c) ⁵⁰¹C₁₀₀ (5)⁴⁰⁰
(d) ⁵⁰⁰C₁₀₁ (5)³⁹⁹

Ans. a
Given,
(5+x)⁵⁰⁰ + x(5+x)⁴⁹⁹ + x²(5+x)⁴⁹⁸ + ...... x⁵⁰⁰
This is a G.P. with first term (5+x)⁵⁰⁰
Common ratio  and 501 terms present.


Coefficient of x¹⁰¹ in (5 + x)⁵⁰¹ is = ⁵⁰¹C₁₀₁.5⁴⁰⁰
∴ In (1/5)((5+x)⁵⁰⁰−x⁵⁰¹) coefficient of x¹⁰¹ is = (1/5).⁵⁰¹C₁₀₁.5⁴⁰⁰
= ⁵⁰¹C₁₀₁.5³⁹⁹

Q.11. The remainder when (2021)²⁰²³ is divided by 7 is :    (JEE Main 2022)
(a) 1
(b) 2
(c) 5
(d) 6

Ans. c
(2021)²⁰²³
= (2016 + 5)²⁰²³ [here 2016 is divisible by 7]
= ²⁰²³C₀ (2016)²⁰²³ + .......... + ²⁰²³C₂₀₂₂ (2016) (5)²⁰²² + ²⁰²³C₂₀₂₃ (5)²⁰²³
= 2016 [²⁰²³C₀ . (2016)²⁰²² + ....... + ²⁰²³C₂₀₂₂ . (5)²⁰²²] + (5)²⁰²³
= 2016λ + (5)²⁰²³
= 7 × 288λ + (5)²⁰²³
= 7K + (5)2⁰²³ ...... (1)
Now, (5)²⁰²³
= (5)²⁰²² . 5
= (5³)⁶⁷⁴ . 5
= (125)⁶⁷⁴ . 5
= (126 − 1)⁶⁷⁴ . 5
= 5[⁶⁷⁴C₀ (126)⁶⁷⁴ + ......... − ⁶⁷⁴C₆₇₃ (126) + ⁶⁷⁴C₆₇₄]
= 5 × 126 [⁶⁷⁴C₀(126)⁶⁷³ + ....... − ⁶⁷⁴C₆₇₃] + 5
= 5 . 7 . 18 [⁶⁷⁴C₀(126)⁶⁷³ + ....... − ⁶⁷⁴C_673] + 5
= 7λ + 5
Replacing (5)²⁰²³ in equation (1) with 7λ + 5, we get,
(2021)²⁰²³ = 7K + 7λ + 5
= 7(K + λ) + 5
∴ Remainder = 5

Q.12. If 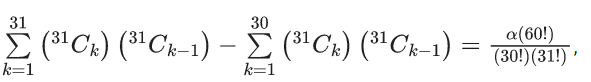 where α ∈ R, then the value of 16α is equal to     (JEE Main 2022)
(a) 1411
(b) 1320
(c) 1615
(d) 1855

Ans. a
Given,

Now,

= (³¹C¹.³¹C₀ +³¹C₂.³¹C₁ +³¹C₃.³¹C₂ +......+ ³¹C₃₁.³¹C₃₀)
= (³¹C₀.³¹C₃₁₋₁+³¹C₁.³¹C₃₁₋₂ +.....+ ³¹C₃₀.³¹C₃₁₋₃₁)
[using ⁿC_r = ⁿC_n−r]
= (³¹C₀.³¹C₃₀ + ³¹C₁.³¹C₂₉ +.....+ ³¹C₃₀.³¹C₀)
= ⁶²C₃₀
Now,

= ⁶⁰C₂₉

Q.13. The term independent of x in the expansion of 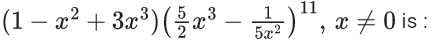    (JEE Main 2022)
(a) 7/40
(b) 33/20
(c) 39/200
(d) 11/50

Ans. b
General term of Binomial expansion

In the term,

Term independent of x is when
(1) 33 − 5r = 0
⇒ r = 335 ∉ integer
(2) 33−5r = −2
⇒ 5r = 35
⇒ r = 7 ∈ integer
(3) 33 − 5r = −3
⇒ 5r = 36
⇒ r = 365 ∉ integer
∴ Only for r = 7 independent of x term possible.
∴ Independent of x term


= 33/200

Q.14. Let n ≥ 5 be an integer. If 9ⁿ − 8n − 1 = 64α and 6ⁿ − 5n − 1 = 25β, then α − β is equal to     (JEE Main 2022)
(a) 1 + ⁿC₂ (8 − 5) + ⁿC₃ (8² − 5²) + ...... + ⁿC_n (8^{n − 1} − 5^{n − 1})
(b) 1 + ⁿC₃ (8 − 5) + ⁿC₄ (8² − 5²) + ...... + ⁿC_n (8^{n − 2} − 5^{n − 2})
(c) ⁿC₃ (8 − 5) + ⁿC₄ (8² − 5²) + ...... + ⁿCⁿ (8^{n − 2} − 5^{n − 2})
(d) ⁿC₄ (8 − 5) + ⁿC₅ (8² − 5²) + ...... + ⁿC_n (8^{n − 3} − 5^{n − 3})

Ans. c
Given,
9ⁿ - 8n - 1 = 64α


= ⁿC₂ + ⁿC₃.8 + ⁿC₄.8² + ..... ⁿC_n.8ⁿ⁻²
Also given,

6ⁿ - 5n - 1 = 25β

= ⁿC₂ + ⁿC₃.5 + ⁿC₄.5² +.....+ ⁿC_n.5ⁿ⁻²
∴ α−β
= (ⁿC₂ + ⁿC₃.8 + ⁿC₄.8² +....+ ⁿC_n.8ⁿ⁻²) − (ⁿC₂ + ⁿC₃.5 + ⁿC₄.5² +....+ ⁿC_n.5ⁿ⁻²)

= ⁿC₃. (8 - 5) + ⁿC₄. (8² - 5²) + .... + ⁿC_n (8^n-2 - 5^n-2)

Q.15. If the constant term in the expansion of 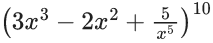 is 2^k.l, where l is an odd integer, then the value of k is equal to:    (JEE Main 2022)
(a) 6
(b) 7
(c) 8
(d) 9

Ans. d
Note : Multinomial Theorem :
The general term of (x₁ + x₂ +...+ x_n)ⁿ the expansion is

where n₁ + n₂ + ..... + n_n = n
Given,

Now constant term in  

∴ Coefficient of  is

where n₁ + n₂ + n₃ = 0
For coefficient of x⁵⁰ :
8n₁ + 7n₂=50
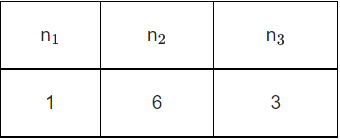
∴ Possible values of n₁, n₂ and n₃ are

∴ Coefficient of x⁵⁰

= 5 × 3 × 8 × 7 × 3 × 5³ × 2⁶
= 7 × 5⁴ × 3² × 2⁹
= 2^k.l
∴ l = 7 × 5⁴ × 3² = An odd integer
and 2^k = 2⁹
⇒ k = 9

Q.16. If 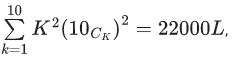 then L is equal to _____.     (JEE Main 2022)

Ans. 221
Given,

⇒ L = 221

Q.17. Let the ratio of the fifth term from the beginning to the fifth term from the end in the binomial expansion of 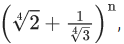 in the increasing powers of  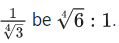If the sixth term from the beginning is  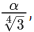then α is equal to _________.    (JEE Main 2022)

Ans. Fifth term from beginning
Fifth term from end = (n−5+1)^th term from begin
Given




⇒ α = 84.

Q.18. If 1+(2+⁴⁹C₁+⁴⁹C₂ +...+⁴⁹C₄₉)(⁵⁰C₂+⁵⁰C₄ +...+ ⁵⁰C₅₀) is equal to 2ⁿ⋅m, where m is odd, then n + m is equal to ______.    (JEE Main 2022)

Ans. 99
l = 1+(1+⁴⁹C₀+⁴⁹C₁ +....+ ⁴⁹C₄₉)(⁵⁰C₂+⁵⁰C₄ +....+ ⁵⁰C₅₀)
As ⁴⁹C₀+⁴⁹C₁ +.....+ ⁴⁹C₄₉ = 2⁴⁹
and ⁵⁰C₀+⁵⁰C₂ +....+ ⁵⁰C₅₀ = 2⁴⁹
⇒ ⁵⁰C₂+⁵⁰C₄ +....+ ⁵⁰C₅₀ = 2⁴⁹−1
∴ l = 1+(2⁴⁹+1)(2⁴⁹−1) = 2⁹⁸
∴ m = 1 and n = 98
m + n = 99

Q.19. Let the coefficients of the middle terms in the expansion of   respectively form the first three terms of an A.P. If d is the common difference of this A.P. , then 50 - (2d/β²) is equal to __________.     (JEE Main 2022)

Ans. 57
Coefficients of middle terms of given expansions are  form an A.P.
∴ 2.2(−3β) = β²−(5β³/2)
⇒ −24 = 2β−5β²
⇒ 5β²−2β−24 = 0
⇒ 5β²−12β+10β−24 = 0
⇒ β(5β−12)+2(5β−12) = 0
β = 12/5
d = −6β − β²

Q.20. Let for the 9^th term in the binomial expansion of (3+6x)ⁿ, in the increasing powers of 6x, to be the greatest for x = 3/2, the least value of n is n₀. If k is the ratio of the coefficient of x⁶ to the coefficient of x3, then k+n₀ is equal to :   (JEE Main 2022)

Ans. 24
(3+6x)ⁿ = 3ⁿ(1+2x)ⁿ
If T₉ is numerically greatest term
∴ T₈ ≤ T₉ ≤ T₁₀

72 ≤ 27(n−7) and 27 ≥ 9(n−8)
(29/3) ≤ n and n ≤ 11
∴ n₀ = 10
For (3+6x)¹⁰
T_r+1 = ¹⁰C_r
3^{10 − r}(6x)_r
For coeff. of x⁶
r = 6 ⇒ ¹⁰C6₃⁴.6⁶
For coeff. of x³
r = 3 ⇒ ¹⁰C₃3⁷.6³

⇒ k = 14
∴ k + n₀ = 24.

Q.21. If the coefficients of x and x² in the expansion of (1+x)^p(1−x)^q, p, q ≤ 15, are −3 and −5 respectively, then the coefficient of x³ is equal to ______.    (JEE Main 2022)

Ans. 23
Coefficient of x in (1+x)^p(1−x)^q
−^pC₀^qC₁ + ^pC₁^qC₀ = −3 ⇒ p−q = −3
Coefficient of x² in (1+x)^p(1−x)^q
pC₀^qC₂ − ^pC₁^qC₁ + ^pC₂^qC₀ = −5

⇒ q =11, p = 8
Coefficient of x³ in (1+x)⁸(1−x)¹¹
=−¹¹C₃+⁸C₁¹¹C₂−⁸C₂¹¹C₁+⁸C₃ = 23

Q.22. If the maximum value of the term independent of t in the expansion of 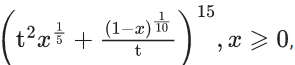 is K, then 8 K is equal to ______.    (JEE Main 2022)

Ans. 6006
General term of

Term will be independent of t when 30 − 3r = 0 ⇒ r = 10
∴ T₁₀₊₁ = T₁₁ will be independent of t

T₁₁ will be maximum when x(1−x) is maximum.
Let f(x) = x(1−x) = x−x²
f(x) is maximum or minimum when f′(x) = 0
∴ f′(x) = 1−2x
For maximum/minimum f′(x) = 0
∴ 1 − 2x = 0
⇒ x = 12
Now, f″(x) = −2 < 0
∴ At x = 1/2, f(x) maximum
∴ Maximum value of T₁₁ is


= 6006

Q.23. The remainder on dividing 1 + 3 + 3² + 3³ + ..... + 3²⁰²¹ by 50 is ____.    (JEE Main 2022)

Ans. 4
Given,
1+3+3²+3³ +.....+ 3²⁰²¹
= 3⁰+3¹+3²+3³ +....+ 3²⁰²¹
This is a G.P with common ratio = 3






=50k+5054
=50k+50×101+4
=50[k+101]+4
=50k′+4
∴ By dividing 50 we get remainder as 4.

Q.24. Let C_r denote the binomial coefficient of x^r in the expansion of (1+x)¹⁰. If for α, β ∈ R, C₁+3.2C₂+5.3C₃ + ....... upto 10 terms 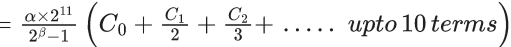  then the value of α + β is equal to ______.    (JEE Main 2022)

Ans. 286
Given,
C₁ + 3.2C₂ + 5.3C₃+ ...... upto 10 terms

Now,
L.H.S. :-C₁+3.2C₂+5.3C₃+ ...... upto 10 terms
=1.1C₁+3.2C₂+5.3C₃+ ..... upto 10 terms




= n.(n−1).2ⁿ⁻²+n.2ⁿ⁻¹]
= 2(n(n−1)2ⁿ⁻²+n.2ⁿ⁻¹)−n.2ⁿ⁻¹
Put n =10
= 2(10.9.2⁸+10.2⁹)−10.2⁹
= 45.2¹⁰+10.2¹⁰−5.2¹⁰
= 2¹⁰(45+10−5)
= 2¹⁰.(50)
= 25.211
R.H.S. :-



Putting value of n=10, we get

Using L.H.S. = R.H.S.

By comparing both sides,

and
⇒ 2¹¹ = 2^β
⇒ β = 11
∴ α + β = 275 + 11 = 286.

Q.25. If the sum of the co-efficient of all the positive even powers of x in the binomial expansion of 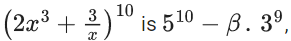 then β is equal to ______.     (JEE Main 2022)

Ans. 83
Given, Binomial Expansion

General term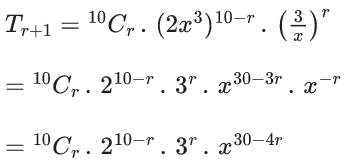
 
For positive even power of x, 30 − 4r should be even and positive.
For r = 0, 30 − 4 × 0 = 30 (even and positive)
For r = 1, 30 − 4 × 1 = 26 (even and positive)
For r = 2, 30 − 4 × 2 = 22 (even and positive)
For r = 3, 30 − 4 × 3 = 18 (even and positive)
For r = 4, 30 − 4 × 4 = 14 (even and positive)
For r = 5, 30 − 4 × 5 = 10 (even and positive)
For r = 6, 30 − 4 × 6 = 6 (even and positive)
For r = 7, 30 − 4 × 7 = 2 (even and positive)
For r = 8, 30 − 4 × 8 = −2 (even but not positive)
So, for r = 1, 2, 3, 4, 5, 6 and 7 we can get positive even power of x.
∴ Sum of coefficient for positive even power of x
= ¹⁰C₀.2¹⁰.3⁰ + ¹⁰C₁.2⁹.3¹ +¹⁰C₂.2⁸.3² + ¹⁰C₃.2⁷.3³ + ¹⁰C₄.2⁶.3⁴ + ¹⁰C₅.2⁵.3⁵ + ¹⁰C₆.2⁴.3⁶ + ¹⁰C₇.2³.3⁷
= ¹⁰C₁₀.2¹⁰.3⁰ + ¹⁰C₁.2⁹.3¹ +.....+ ¹⁰C₁₀.2⁰.3¹⁰−[¹⁰C₈.2².3⁸+¹⁰C₉.2.3⁹+¹⁰C₁₀.2⁰.3¹⁰]
= (2+3)¹⁰ − [45.4.3⁸ + 10.2.3⁹ + 1.1.3¹⁰]
= 5¹⁰ − [60 × 3⁹ + 20.3⁹ + 3.3⁹]
= 5¹⁰ − (60 + 20 + 3)39
= 5₁₀ − 83.3⁹
∴ β = 83.

Q.26. If (⁴⁰C₀)+(⁴¹C₁)+(⁴²C₂)+.....+(⁶⁰C₂₀) = (m/n)⁶⁰C₂₀ m and n are coprime, then m + n is equal to ______.     (JEE Main 2022)

Ans. 102
Here property used is
ⁿC^r + ⁿC_r+1 = ⁿ⁺¹C_r+1
Given,
As ⁴⁰C₀ = ⁴¹C₀ =1
So, we replace ⁴⁰C₀ with ⁴¹C₀.



∴ m = 61 and n = 41
∴ m + n = 61 + 41 = 102

Q.27. Let 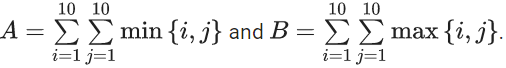 Then A + B is equal to _____.     (JEE Main 2022)

Ans. 1100

= {1, 1} {1, 2} {1, 3} ..... {1, 10}
{2, 1} {2, 2} {2, 3} ..... {2, 10}
{3, 1} {3, 2} {3, 3} ..... {3, 10}
⋮
{10, 1} {10, 2} {10, 3} ..... {10, 10}
Now,
= minimum between i and j in all sets and summation of all those values.
and
= maximum between i and j in all sets and summation of all those values.
For 1 :
1 is minimum in sets = {1, 1}, {1, 2}, {1, 3}, {1, 4}, {1, 5}, {1, 6}, {1, 7}, {1, 8}, {1, 9}, {1, 10}, {2, 1}, {3, 1}, {4, 1}, {5, 1}, {6, 1}, {7, 1}, {8, 1}, {9, 1}, {10, 1}
∴ 1 is minimum in 19 sets
1 is maximum in {1, 1} sets.
∴ 1 is maximum and minimum in total 20 sets.
∴ Sum of 1 in all those sets = 1 × 20 = 20
For 2 : 2 is minimum in sets = {2, 2}, {2, 3}, {2, 4}, {2, 5}, {2, 6}, {2, 7}, {2, 8}, {2, 9}, {2, 10}, {3, 2}, {4, 2}, {5, 2}, {6, 2}, {7, 2}, {8, 2}, {9, 2}, {10, 2}
∴ 2 is minimum in 17 sets
2 is maximum in sets = {1, 2}, {2, 1}, {2, 2}
∴ 2 is maximum and minimum in 20 sets.
∴ Sum of 2 in all those sets = 2 × 20 = 40
Similarly 3 is maximum and minimum in 20 sets.
∴ Sum of 3 in all those sets = 20 × 3 = 60
⋮
Similarly, 10 is maximum and minimum in 20 sets.
∴ Sum of 10 in all those sets = 20 × 10 = 200
∴ A + B = 20 + 20 × 2 + 20 × 3 + ....... + 20 × 10
= 20(1 + 2 + 3 + ...... + 10)
= 20 × ((10×11)/2)
= 1100

Q.28. If the coefficient of x¹⁰ in the binomial expansion of 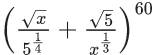 is 5^k.l, where l, k ∈ N and l is co-prime to 5, then k is equal to _______.    (JEE Main 2022)

Ans. 5
Given Binomial Expansion
∴ General term

For x¹⁰ term,

⇒ 5r = 120
⇒ r = 24
∴ Coefficient of  


It is given that,

Also given that, l is coprime to 5 means l can't be multiple of 5. So we have to find all the factors of 5 in 60!, 24! and 36!
[Note : Formula for exponent or degree of prime number in n!.
Exponent of p in n! =  ..... until 0 comes here p is a prime number.]
∴ Exponent of 5 in 60!

= 12+2+0+ .....=14
Exponent of 5 in 24!

= 4 + 0 + 0 ...... = 4
Exponent of 5 in 36!

= 7 + 1 + 0 ......= 8
∴ From equation (1), exponent of 5 overall

⇒ 5⁵ = 5^k
⇒ k = 5

Q.29. If the sum of the coefficients of all the positive powers of x, in the Binomial expansion of 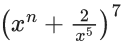 is 939, then the sum of all the possible integral values of n is ______.      (JEE Main 2022)

Ans. 57
Given, Binomial expression is
∴ General term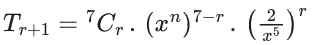  

For positive power of x,
7n − nr −5r > 0
⇒ 7n > r(n + 5)
⇒ r < (7n/(n+5))

As r represent term of binomial expression so r is always integer.
Given that sum of coefficient is 939.
When r = 0,
sum of coefficient = ⁷C₀.2⁰ = 1
when r = 1,
sum of coefficient = ⁷C₀.2⁰+⁷C₁.2¹ = 1+14 = 15
when r = 2,
sum of coefficient
= ⁷C₀.2⁰+⁷C₁.2¹+⁷C₂.2²
= 1+14+84
= 99
when r = 3,
sum of coefficient
= ⁷C₀.2⁰ + ⁷C₁.2¹ + ⁷C₂.2² + ⁷C₃.2³
= 1+14+84+280
= 379
when r=4,
sum of coefficient
= ⁷C₀.2⁰ + ⁷C₁.2¹ + ⁷C₂.2² + ⁷C₃.2³ + ⁷C₄.2⁴
= 1+14+84+280+560
= 939
∴ For r = 4 sum of coefficient = 939
To get value of r = 4, value of (7n/(n+5)) should be between 4 and 5.

⇒ 4n + 20 < 7n < 5n + 25
∴ 4n + 20 < 7n
⇒ 3n > 20
⇒ n > 20/3
⇒ n > 6.66
and
7n < 5n +25
⇒ 2n < 25
⇒ n < 12.5
∴ 6.66 < n < 12.5
∴ Possible integer values of n = 7,8,9,10,11,12
∴ Sum of values of n=7+8+9+10+11+12 = 57

Q.30. The number of positive integers k such that the constant term in the binomial expansion of 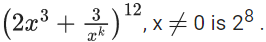 l, where l is an odd integer, is _______.    (JEE Main 2022)

Ans. 2
Given Binomial expression is
General term,

= (¹²C_r.²r.3^12−r).x^3r−12k+kr
For constant term, 3r−12k+kr = 0
⇒ k(12−r) = 3r
⇒ k = 3r/(12−r)
For r = 1, k = (3/11) (not integer)
For r = 2, k = (6/10) (not integer)
For r = 3, k = (9/9) = 1 (integer)
For r = 6, k = (18/6) = 3 (integer)
For r = 8, k = (24/4) = 6 (integer)
For r = 9, k = (27/3) = 9 (integer)
For r = 10, k = (30/2) = 15 (integer)
For r = 11, k = (33/1) = 33 (integer)
So, for r = 3, 6, 8, 9, 10 and 11 k is positive integer.
When k = 1 then r = 3 and constant term is = ¹²C₃ . 2³ . 3⁹

= 2.11.2.5.2³.3⁹
= 11.5.2⁵.3⁹
= 2⁵.(55.3⁹)
= 2⁵(l)
≠ 2⁸.l
When x = 3 then r = 6 and constant term = ¹²C₆ . 2⁶ . 3⁶

= 2⁸.231.36
= 2⁸(l)
When k = 6 then r = 8 and constant term = ¹²C₈ . 2⁸ . 3⁴

= 2⁸.55.3⁶
= 2⁸(l)
When x = 9 then r = 9 and constant term = ¹²C₉.2⁹.3³

= 2¹¹ . 55 . 3³
Here power of 2 is 11 which is greater than 8. So, k = 9 is not possible.
Similarly for k = 15 and k = 33, 2⁸.l form is not possible.
∴ k = 3 and k = 6 is accepted.
∴ For 2 positive integer value of k, 2⁸ . l form of constant term possible.

Q.31. Let the coefficients of x⁻¹ and x⁻³ in the expansion of  be m and n respectively. If r is a positive integer such that mn² = ¹⁵C_r.2^r, then the value of r is equal to __________.    (JEE Main 2022)

Ans. 5
Given, Binomial expansion
∴ General Term

For x⁻¹ term;
1/5(15-2r) = -1
⇒ 15 − 2r = −5
⇒ 2r = 20
⇒ r = 10
m is the coefficient of x⁻¹ term,
∴ m = ¹⁵C₁₀.2¹⁵⁻¹⁰.(−1)¹⁰
= ¹⁵C₁₀.2⁵
For x−3 term;
1/5(15-2r) = -3
⇒ 15−2r = −15
⇒ 2r = 30
⇒ r = 15
n is the coefficient of x⁻³ term,
∴ n = ¹⁵C₁₅.2¹⁵⁻¹⁵.(−1)¹⁵
= 1.1.−1
= −1
Given,
mn² = ¹⁵C_r.2^r
⇒ ¹⁵C₁₀.2⁵.(1)² = ¹⁵C_r.2^r [putting value of m and n]
⇒ ¹⁵C₁₅₋₁₀.2⁵ = ¹⁵C_r.2^r
⇒ ¹⁵C₅.2⁵ = ¹⁵C_r.2^r
Comparing both side, we get
r = 5.

Q.32. 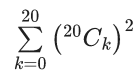  is equal to :    (JEE Main 2021)
(a) 40C21
(b) 40C19
(c) 40C20
(d) 41C20

Ans. c


= ⁴⁰C₂₀
Using the formula :
(ⁿC₀)² + (ⁿC₁)² + (ⁿC₂)² +....+ (ⁿC_n)² = ²ⁿC_n

Q.33. If ²⁰C_r is the co-efficient of x^r in the expansion of (1 + x)²⁰, then the value of 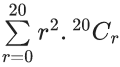 is equal to :     (JEE Main 2021)
(a) 420×2¹⁹
(b) 380×2¹⁹
(c) 380×2¹⁸
(d) 420×2¹⁸

Ans. d



⇒ 20 × 19.2¹⁸ + 20.2¹⁹
⇒ 420 × 2¹⁸

Q.34. If the coefficients of x⁷ 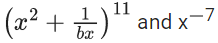in  in 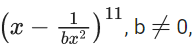 are equal, then the value of b is equal to :     (JEE Main 2021)
(a) 2
(b) -1
(c) 1
(d) -2

Ans. c
Coefficient of x⁷ in
General Term =

22 − 3r = 7
r = 5
∴ Required Term =


11−3r=−7 ∴ r=6
∴ Required Term =
According to the question,

Since, b ≠ 0 ∴ b = 1

Q.35. The lowest integer which is greater than 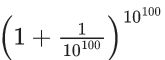 is ____.     (JEE Main 2021)
(a) 3
(b) 4
(c) 2
(d) 1

Ans. a

Let x = 10¹⁰⁰

⇒ P = (1 + (1/x)^x

(upto 10¹⁰⁰ + 1 terms)




⇒ P = 2 + (positive value less than e − 2)
⇒ P ∈ (2, 3)
⇒ least integer value of P is 3

Q.36. If the greatest value of the term independent of 'x' in the expansion of 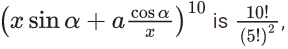 then the value of 'a' is equal to :     (JEE Main 2021)
(a) -1
(b) 1
(c) -2
(d) 2

Ans. d

r = 0, 1, 2, ......., 10
T_{r + 1} will be independent of x when 10 − 2r = 0 ⇒ r = 5


will be greatest when sin2α = 1

Q.37. The sum of all those terms which are rational numbers in the expansion of (2^1/3 + 3^1/4)¹² is :      (JEE Main 2021)
(a) 89
(b) 27
(c) 35
(d) 43

Ans. d
T_r+1 = ¹²C_r(2^1/3)^r.(3^1/4)¹²⁻⁴
T_{r + 1} will be rational number when r = 0, 3, 6, 9, 12 & r = 0, 4, 8, 12
⇒ r = 0, 12
T₁ + T₁₃ = 1 × 3³ + 1 × 2⁴ × 1
= 24 + 16 = 43

Q.38. A possible value of 'x', for which the ninth term in the expansion of 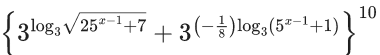 in the increasing powers of  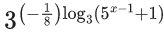is equal to 180, is :      (JEE Main 2021)
(a) 0
(b) -1
(c) 2
(d) 1

Ans. d
¹⁰C₈(25^(x−1) + 7) × (5^(x−1) + 1)⁻¹ = 180


⇒ t = 1, 3 = 5^{x − 1}
⇒ x − 1 = 0 (one of the possible value).
⇒ x = 1

Q.39. If b is very small as compared to the value of a, so that the cube and other higher powers of b/a can be neglected in the identity 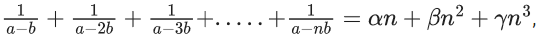  then the value of γ is :     (JEE Main 2021)
(a)
(b)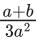
(c)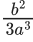
(d)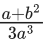

Ans. c
(a − b)⁻¹ + (a − 2b)⁻¹ +....+ (a − nb)⁻¹

So, γ = b²/3a³

Q.40. For the natural numbers m, n, if (1−y)^m(1+y)ⁿ = 1 + a₁y + a₂y² +....+ a_m+n y^m+n and a₁ = a₂ =10, then the value of (m + n) is equal to :    (JEE Main 2021)
(a) 88
(b) 64
(c) 100
(d) 80

Ans. d
(1−y)^m(1+y)ⁿ = 1 + a₁y + a₂y² +....+ a_{m + n} y^m+n
Given, (a₁ = a₂ = 10)(1 − my + ^mC₂y² +.....)(1 + ny + ⁿC₂y² +.....) = 1 + a₁y + a₂y² +....
⇒ n − m = 10 ..... (i)
⇒ ^mC₂ +ⁿC₂ − mn = 10...... (ii)


⇒ m² − m + m² + 19m + 90−2(m² + 10m) = 20
⇒ 18m + 90 − 20m = 20
⇒ 2m = 70
⇒ m = 35 & n = 45

Q.41. The coefficient of x²⁵⁶ in the expansion of (1 − x)¹⁰¹ (x² + x + 1)¹⁰⁰ is :     (JEE Main 2021)
(a) ¹⁰⁰C₁₆
(b) ¹⁰⁰C₁₅
(c) -¹⁰⁰C₁₆
(d) -¹⁰⁰C₁₅

Ans. b
(1−x)¹⁰¹(x²+x+1)¹⁰⁰
Coefficient of x²⁵⁶ = [(1−x)(1+x+x²)]¹⁰⁰(1−x)=(1−x³)¹⁰⁰(1−x)
⇒ (¹⁰⁰C₀ − ¹⁰⁰C₁x³ + ¹⁰⁰C₂x⁶ − ¹⁰⁰C₃x⁹...)(1−x)
∑(−1)^r100C_rx^3r(1−x)
⇒ 3r = 256 or 255 ⇒ r = (256/3) (Reject)
r = 85
Coefficient = ¹⁰⁰C₈₅ = ¹⁰⁰C₁₅

Q.42. Let (1 + x + 2x²)²⁰ = a₀ + a₁x + a₂x² + .... + a₄₀x⁴⁰. Then a₁ + a₃ + a₅ + ..... + a₃₇ is equal to     (JEE Main 2021)
(a) 2²⁰(2²⁰ − 21)
(b) 2¹⁹(2²⁰ − 21)
(c) 2¹⁹(2²⁰ + 21)
(d) 2²⁰(2²⁰ + 21)

Ans. b
(1+x+2x²)²⁰ = a₀ + a₁x + a₂x² +....+ a₄₀x⁴⁰
Put x = 1
⇒ 4²⁰ = a₀ + a₁ +.......+ a₄₀ ..... (i)
Put x = −1
⇒ 2²⁰ = a₀−a₁ +.......+ −a₃₉ + a₄₀ ..... (ii)
by (i) − (ii) we get,
4²⁰ − 2²⁰ = 2(a₁ + a₃ +......+ a₃₇ + a₃₉)
⇒ a₁ + a₃ +......+ a₃₇ = 2³⁹ − 2¹⁹ − a₃₉ ..... (iii)
a₃₉ = coeff. x³⁹ in (1 + x + 2x²)²⁰

= 20.2¹⁹
∴ a₁ + a₃ +......+ a₃₇ = 2³⁹ − 2¹⁹.21
⇒ 2¹⁹ (2²⁰ - 21)

Q.43. The value of 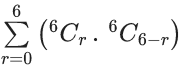 is equal to :    (JEE Main 2021)
(a) 924
(b) 1024
(c) 1124
(d) 1324

Ans. a
Given,

= ⁶C₀.⁶C₆ + ⁶C₁.⁶C₅ +...+ ⁶C₆.⁶C₀
Now,
=(⁶C₀ + ⁶C₁x + ⁶C₂x² +...+ ⁶C₆x⁶)(⁶C₀ + ⁶C₁x + ⁶C₂x² +...+ ⁶C₆x⁶)
Comparing coefficient of x⁶ both sides
⁶C₀.⁶C₆+⁶C₁.⁶C₅+...+⁶C₆.⁶C₀
= ¹²C₆ = 924

Q.44. If the fourth term in the expansion of 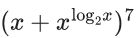 is 4480, then the value of x where x ∈ N is equal to :     (JEE Main 2021)
(a) 3
(b) 1
(c) 4
(d) 2

Ans. d

take log w.r.t. base 2 we get,

Let log₂x = y
4y + 3y² = 7
⇒ y = 1,((−7)/3)
⇒ log₂x = 1, (−7)/3
⇒ x = 2, x = 2^−7/3

Q.45. If n is the number of irrational terms in the expansion of (3^1/4 + 5^1/8)⁶⁰, then (n − 1) is divisible by :     (JEE Main 2021)
(a) 30
(b) 8
(c) 7
(d) 26

Ans. d
T_r+1 = ⁶⁰C_r(3^1/4)^60−r(5^1/8)^r
rational if (60−r)/4, r/8, both are whole numbers, r ∈ {0,1,2,......60}
((60−r)/4) ∈ W ⇒ r ∈ {0,4,8,....60}
and (r/8) ∈ W ⇒ r ∈ {0,8,16,.....56}
∴ Common terms r ∈ {0,8,16,.....56}
So, 8 terms are rational
Then Irrational terms = 61 − 8 = 53 =n
∴ n − 1 = 52 = 13  ×2²
Factors 1, 2, 4, 13, 26, 52

Q.46. The maximum value of the term independent of 't' in the expansion of 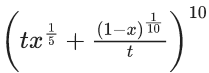 where x ∈ (0, 1) is :     (JEE Main 2021)
(a)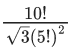
(b)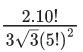
(c)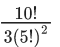
(d)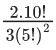

Ans. b


⇒ 10−2r = 0 ⇒ r =5

At maximum,
⇒ 1−x = x/2 ⇒ 3x = 2 ⇒ x = 2/3

Q.47. If n ≥ 2 is a positive integer, then the sum of the series ⁿ⁺¹C₂+2(²C₂ + ³C₂ + ⁴C₂ +...+ ⁿC₂) is :    (JEE Main 2021)
(a)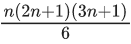
(b)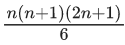
(c)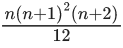
(d)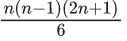

Ans. b
ⁿ⁺¹C₂ + 2(²C₂ + ³C₂ + ⁴C₂ +........+ ⁿC₂)
ⁿ⁺¹C₂ + 2(³C₂ + ³C₂ + ⁴C₂ +........+ ⁿC₂)
use {ⁿC_r+1 + ⁿC_r = ⁿ⁺¹C_r}
= ⁿ⁺¹C₂ + 2(⁴C₃ + ⁴C₂ + ⁵C³ +........+ ⁿC₂)
= ⁿ⁺¹C₂ + 2(⁵C₃ + ⁵C₂ +........+ ⁿC₂)
.....
= ⁿ⁺¹C₂ + 2(ⁿC₃ + ⁿC₂)
= ⁿ⁺¹C₂ + 2.ⁿ⁺¹C₃

Q.48. The value of -¹⁵C₁ + 2.¹⁵C₂ – 3.¹⁵C₃ + ... - 15.¹⁵C₁₅ + ¹⁴C₁ + ¹⁴C₃ + ¹⁴C₅ + ...+ ¹⁴C₁₁ is :     (JEE Main 2021)
(a) 2¹³ - 13
(b) 2¹⁶ - 1
(c) 2¹⁴
(d) 2¹³- 14

Ans. d
−¹⁵C₁ + 2.¹⁵C₂ − 3.¹⁵C₃ +..... −15.¹⁵C₁₅



=15(−¹⁴C₀ + ¹⁴C₁ − ¹⁴C₂ +....−¹⁴C₁₄)
=15(0)=0
We know,
⇒ 2^{14 - 1} = ¹⁴C₁+¹⁴C₃+¹⁴C₅....+¹⁴C₁₃
⇒ 2¹³ = ¹⁴C₁ +¹⁴C₃ + ¹⁴C₅ ....+ ¹⁴C₁₃
Also let, S = ¹⁴C₁ + ¹⁴C₃ + ¹⁴C₅ + ...+ ¹⁴C₁₁
⇒ S + ¹⁴C₁₃ = ¹⁴C₁ + ¹⁴C₃ + ¹⁴C₅ + ...+ ¹⁴C₁₁ + ¹⁴C₁₃
⇒ S + ¹⁴C₁₃ = 2¹³
⇒ S + 14 = 2¹³
⇒ S = 2¹³ - 14
Other Method :
We know, (1−x)¹⁵ = ¹⁵C₀ − ¹⁵C₁x + ¹⁵C₂x² −.....− ¹⁵C₁₅x¹⁵
Differentiating both sides with respect to x,
15(1−x)¹⁴(−1)=−¹⁵C₁+2¹⁵C₂x−3¹⁵C₃x² +.......− 15¹⁵C₁₅x¹⁴
Put x=1
⇒ 0 = −¹⁵C₁ + 2¹⁵C₂ − 3¹⁵C₃ +....− 15¹⁵C₁₅
We know,
⇒ 2^{14 - 1} = ¹⁴C₁ + ¹⁴C₃ + ¹⁴C₅ .... +¹⁴C₁₃
⇒ 2¹³ = ¹⁴C₁ + ¹⁴C₃ + ¹⁴C₅ ....+ ¹⁴C₁₃
Also let, S = ¹⁴C₁ + ¹⁴C₃ + ¹⁴C₅ + ...+ ¹⁴C₁₁
⇒ S + ¹⁴C₁₃ = ¹⁴C₁ + ¹⁴C₃ + ¹⁴C₅ + ...+ ¹⁴C₁₁ + ¹⁴C₁₃
⇒ S + ¹⁴C₁₃ = 2¹³
⇒ S + 14 = 2¹³
⇒ S = 2¹³ - 14

Q.49. If the sum of the coefficients in the expansion of (x + y)ⁿ is 4096, then the greatest coefficient in the expansion is _____________.    (JEE Main 2021)

Ans. 924
(x + y)ⁿ ⇒ 2ⁿ = 4096
2¹⁰ = 1024 × 2
⇒ 2ⁿ = 2¹²
2¹¹ = 2048
n = 12
2¹² = 4096

= 11×3×4×7
= 924

Q.50. If the coefficient of a⁷b⁸ in the expansion of (a + 2b + 4ab)¹⁰ is K.2¹⁶, then K is equal to _____________.    (JEE Main 2021)

Ans. 315


α + β + γ = 10 ..... (1)
α + γ = 7 .... (2)
β + γ = 8 ..... (3)
(2) + (3) − (1) ⇒ γ = 5
α = 2
β = 3
so coefficients =

= 315 × 216 ⇒ k = 315

Q.51. If (3⁶/4⁴)k is the term, independent of x, in the binomial expansion of 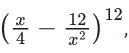 then k is equal to ___________.     (JEE Main 2021)

Ans. 55



Term independent of x ⇒ 12 − 3r = 0 ⇒ r = 4

⇒ k = 55.

Q.52. 3 × 7²² + 2 × 10²² − 44 when divided by 18 leaves the remainder __________.    (JEE Main 2021)

Ans. 15

3(1 + 6)²² + 2 . (1 + 9)²² − 44 = (3 + 2 − 44) = 18 . I
= − 39 + 18 . I
= (54 − 39) + 18(I − 3)
= 15 + 18I₁
⇒ Remainder = 15

Q.53. Let 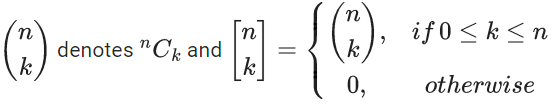 If 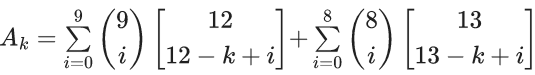 and A₄ − A₃ = 190 p, then p is equal to :    (JEE Main 2021)

Ans. 49

A_k = ²¹C_k + ²¹C_k = 2.²¹C_k
A₄−A₃ = 2(²¹C₄−²¹C₃) = 2(5985−1330)
190p = 2(5985−1330) ⇒ p = 49

Q.54. If the co-efficient of x⁷ and x⁸ in the expansion of (2 + (x/3))ⁿ are equal, then the value of n is equal to _____________.    (JEE Main 2021)

Ans. 55

⇒ n − 7 = 48 ⇒ n = 55

Q.55. Let n ∈ N and [x] denote the greatest integer less than or equal to x. If the sum of (n + 1) terms ⁿC₀,3.ⁿC₁,5.ⁿC₂,7.ⁿC₃ ,..... is equal to 2¹⁰⁰ . 101, then 2[(n−1)/2] is equal to _____.     (JEE Main 2021)

Ans. 98
1. ⁿC₀ + 3.ⁿC₁ + 5.ⁿC₂ +...+ (2n+1).ⁿC_n
T_r = (2r+1)ⁿC_r
S = ∑T_r
S = ∑(2r+1)ⁿC_r = ∑2rⁿC_r + ∑ⁿC_r
S = 2(n.2ⁿ⁻¹)+2ⁿ = 2ⁿ(n+1)
2ⁿ(n+1) = 2¹⁰⁰.101 ⇒ n = 100

Q.56. The term independent of 'x' in the expansion of 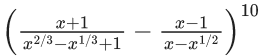, where x ≠ 0, 1 is equal to _______.    (JEE Main 2021)

Ans. 210






[Note: For  term with power m of x is

 
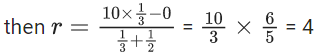
∴ T₅ is the term independent of x.
∴ T₅ = ¹⁰C₄ = 210

Q.57. The ratio of the coefficient of the middle term in the expansion of (1 + x)²⁰ and the sum of the coefficients of two middle terms in expansion of (1 + x)¹⁹ is ______.      (JEE Main 2021)

Ans. 1
Coeff. of middle term in (1 + x)²⁰ = ²⁰C₁₀ & Sum of coeff. of two middle terms in (1 + x)¹⁹ = ¹⁹C₉ + ¹⁹C₁₀
So required ratio =

Q.58. The number of elements in the set {n ∈ {1, 2, 3, ......., 100} | (11)ⁿ > (10)ⁿ + (9)ⁿ} is ________.    (JEE Main 2021)

Ans. 96
11ⁿ >10ⁿ + 9ⁿ
⇒ 11ⁿ − 9ⁿ> 10ⁿ
⇒ (10+1)ⁿ−(10−1)ⁿ>10ⁿ
⇒ 2{ⁿC₁.10ⁿ⁻¹ + ⁿC₃10^{n − 10} + ⁿC₅10^{n − 5} +.....} > 10ⁿ
⇒ 1/5[ⁿC₁10ⁿ + ⁿC₃10^{n − 2} + ⁿC₅10^{n − 4} +.....]>10ⁿ
⇒ 1/5[ⁿC₁+ⁿC₃10⁻² + ⁿC₅10^{− 4} +.....]>1
Clearly the above inequality is true for n ≥ 5
For n = 4, we have
⇒ Inequality does not hold good for n = 1, 2, 3, 4
So, required number of elements ={5, 6, 7, ......., 100} = 96

Q.59. If the constant term, in binomial expansion of 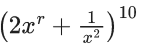 is 180, then r is equal to ______ .     (JEE Main 2021)

Ans. 8

General term = ¹⁰C_R(2x²)^10−Rx^−2R
⇒ 2^10−R10C_R = 180 ....... (1)
& (10 − R)r − 2R = 0



R = 8 or 5 reject equation (1) not satisfied
At R = 8
⇒ 2^{10 − R} × ¹⁰C_R = 180 ⇒ r = 8

Q.60. The number of rational terms in the binomial expansion of  is ____.      (JEE Main 2021)

Ans. 21

T_r+1=¹²⁰C_r(2^1/2)^120−r(5)^r/6
for rational terms r = 6λ
0 ≤ r ≤ 120
So total no of terms are 21.

Q.61. Let ⁿC_r denote the binomial coefficient of x^r in the expansion of 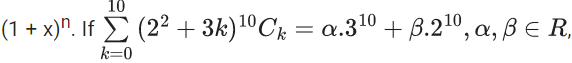 then α + β is equal to ____ .      (JEE Main 2021)

Ans. 19



=  4(2¹⁰)+3.10(2⁹)
= 4(2¹⁰)+3.5.2¹⁰
= 2¹⁰(19)
According to question,
19(2¹⁰) = α.3¹⁰+β.2¹⁰
∴ α = 0, β = 19
⇒ α + β = 19

Q.62. The term independent of x in the expansion of 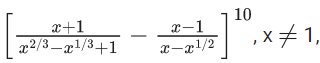 is equal to _____.     (JEE Main 2021)

Ans. 210







For being independent of
Term independent of x = ¹⁰C₄ = 210

Q.63. Let the coefficients of third, fourth and fifth terms in the expansion of 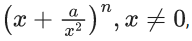 be in the ratio 12 : 8 : 3. Then the term independent of x in the expansion, is equal to _____.     (JEE Main 2021)

Ans. 4




⇒ a(n − 2) = 2 .......... (i)

⇒ a(n − 3) = 32 ........ (ii)
by (i) and (ii) n = 6, a = 12
for term independent of 'x'

Q.64. If (2021)³⁷⁶² is divided by 17, then the remainder is ______.     (JEE Main 2021)

Ans. 4
2021 = 17m - 2
(2021)³⁷⁶² = (17m − 2)³⁷⁶² = multiple of 17 + 2³⁷⁶²
= 17λ + 2² (2⁴)⁹⁴⁰
= 17λ + 4 (17 − 1)⁹⁴⁰
= 17λ + 4 (17μ + 1)
= 17k + 4; (k ∈ I)
∴ Remainder = 4

Q.65. Let n be a positive integer. Let 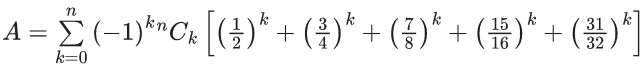 . If 63A = 1 − (1/(2³⁰)), then n is equal to ______.      (JEE Main 2021)

Ans. 6







For n = 6, L.H.S = R.H.S
∴ n = 6

Q.66. Let m, n ∈ N and gcd (2, n) = 1. If 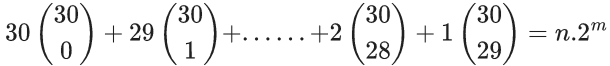 , then n + m is equal to __________.
      (JEE Main 2021)

Ans. 45
30(³⁰C₀) + 29(³⁰C₁) +....+ 2(³⁰C₂₈) + 1(³⁰C₂₉)
= 30(³⁰C3₀) + 29(³⁰C₂₉) +......+ 2(³⁰C₂) + 1(³⁰C₁)



= 30(²⁹C₀ + ²⁹C₁ + ²⁹C₂ +.....+ ²⁹C₂₉)
= 30(2²⁹) = 15(2)³⁰ = n(2)^m
∴ n = 15, m = 30
⇒ n + m = 45

Q.67. The total number of two digit numbers 'n', such that 3ⁿ + 7ⁿ is a multiple of 10, is ______.    (JEE Main 2021)

Ans. 45
∵ 7ⁿ = (10−3)ⁿ = 10k + (−3)ⁿ
7ⁿ + 3ⁿ = 10k + (−3)ⁿ + 3ⁿ

∴ 3ⁿ = 3^2t = (10 − 1)^t
= 10p + (−1)^t
= 10p ± 1
∴ if n = even then 7n + 3n will not be multiply of 10
So if n is odd then only 7n + 3n will be multiply of 10
∴ n = 11, 13, 15, ..........., 99
∴ Ans : 45

Q.68. If the remainder when x is divided by 4 is 3, then the remainder when (2020 + x)²⁰²² is divided by 8 is _______.    (JEE Main 2021)

Ans. 1
Let x = 4k + 3
(2020 + x)²⁰²²
= (2020 + 4k + 3)²⁰²²
= (4(505) + 4k + 3)²⁰²²
= (4P + 3)²⁰²²
= (4P + 4 − 1)²⁰²²
= (4A − 1)^2022
2022C₀(4A)⁰(−1)^{2022 + 2022}C₁(4A)¹(−1)²⁰²¹ + ......
= 1 + 2022(4A)(-1) + .....
= 1 + 8λ
∴ Reminder is 1.

Q.69. For integers n and r, let  The maximum value of k for which the sum 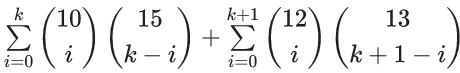 exists, is equal to  _____.     (JEE Main 2021)

Ans. 12
As k is unbounded so maximum value is not defined.
Question will be BONUS.

Q.70. The term independent of x in the expansion of 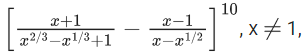 is equal to ______.     (JEE Main 2021)

Ans. 210







For being independent of
Term independent of x = ¹⁰C₄ = 210