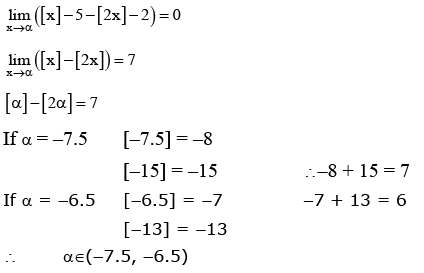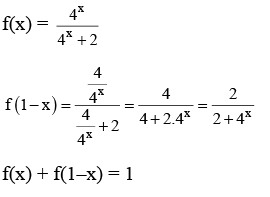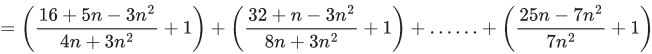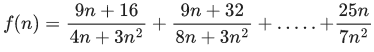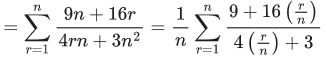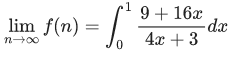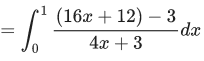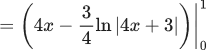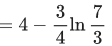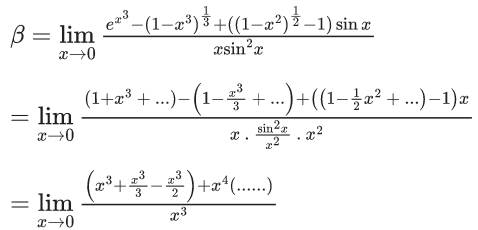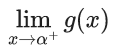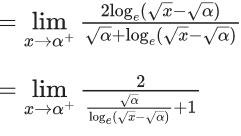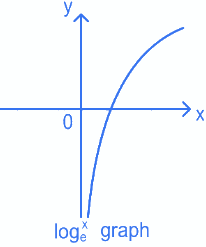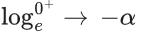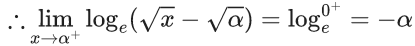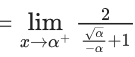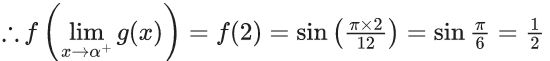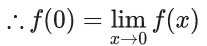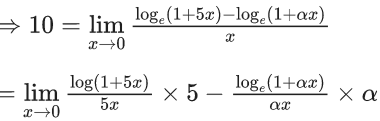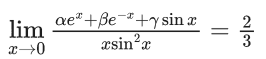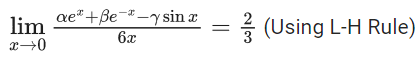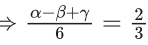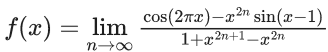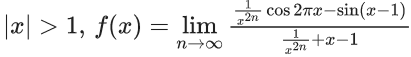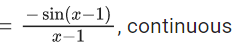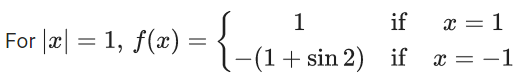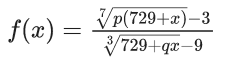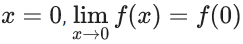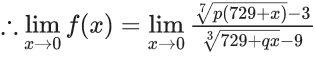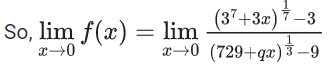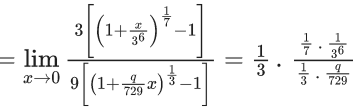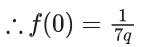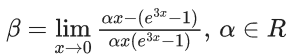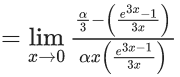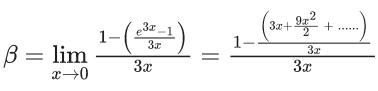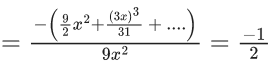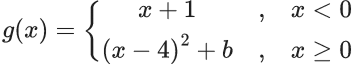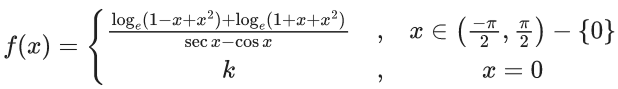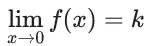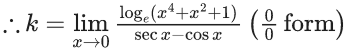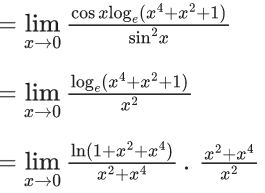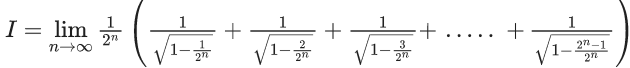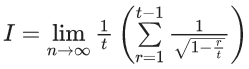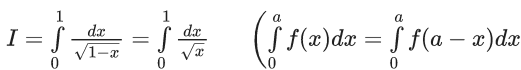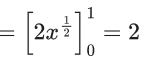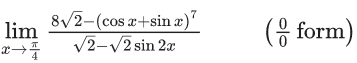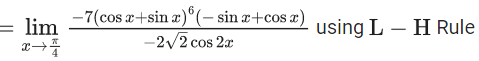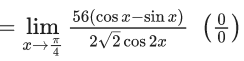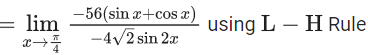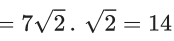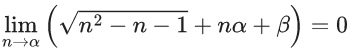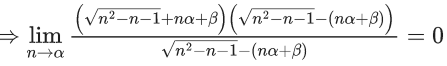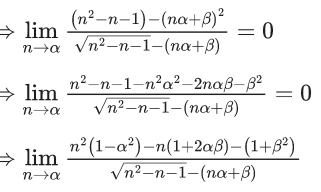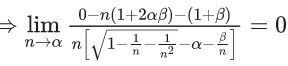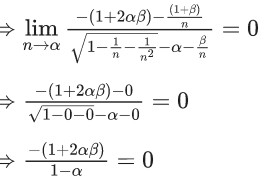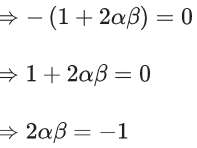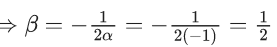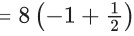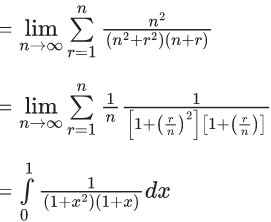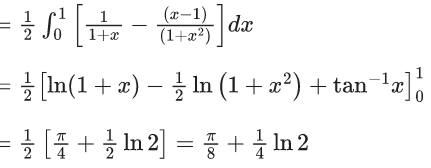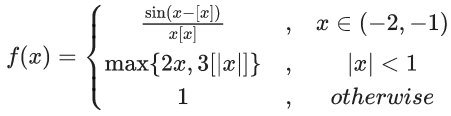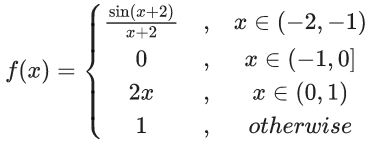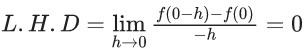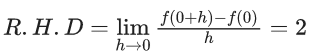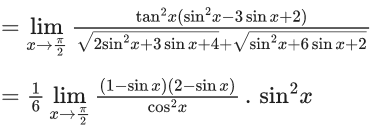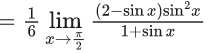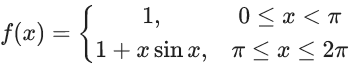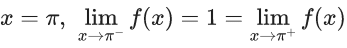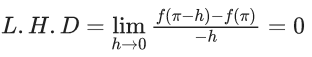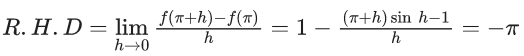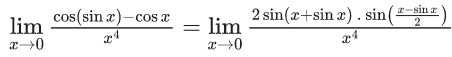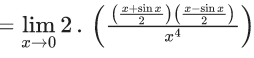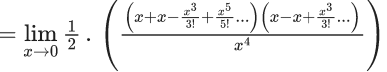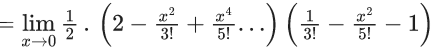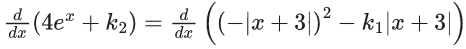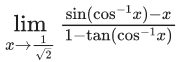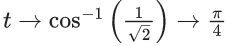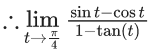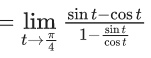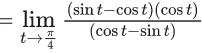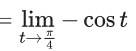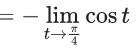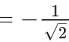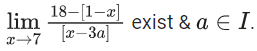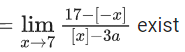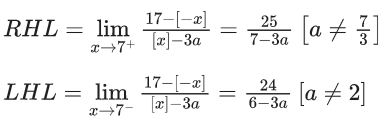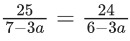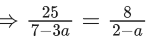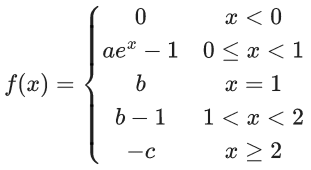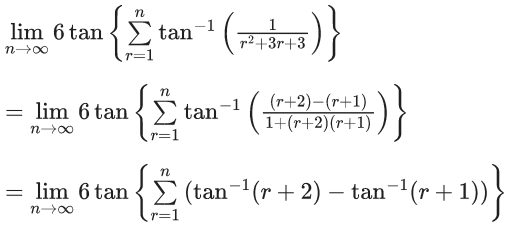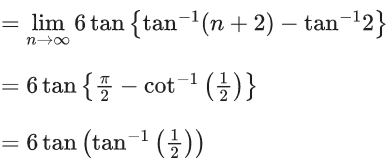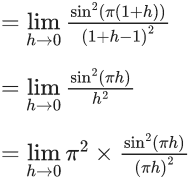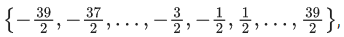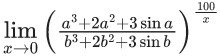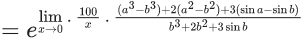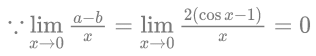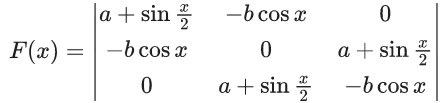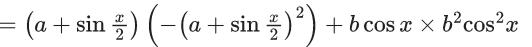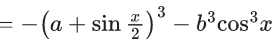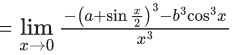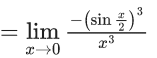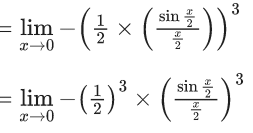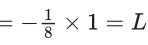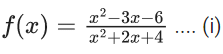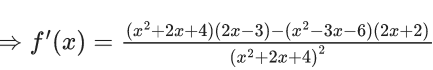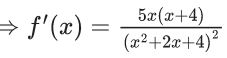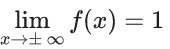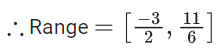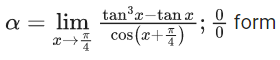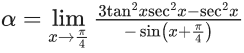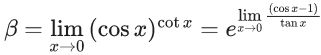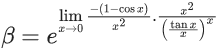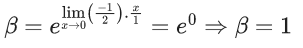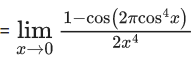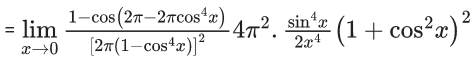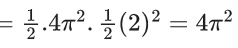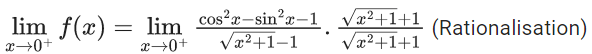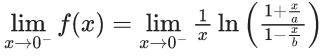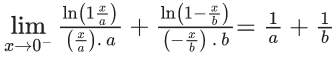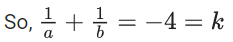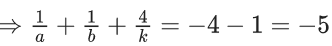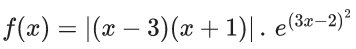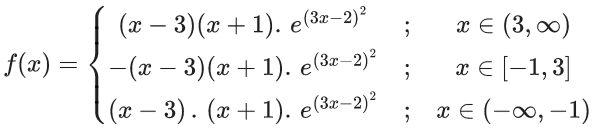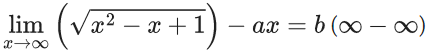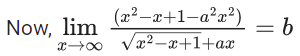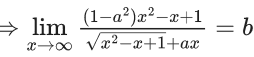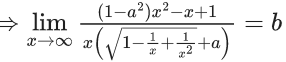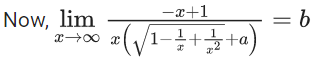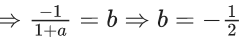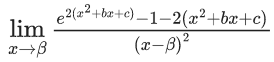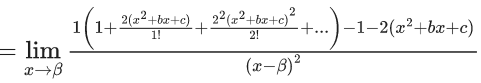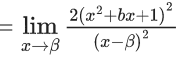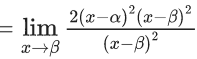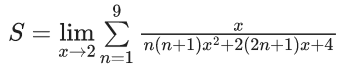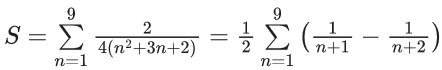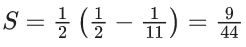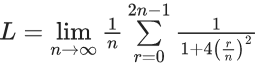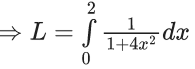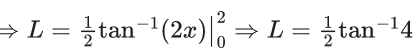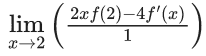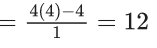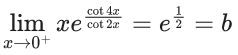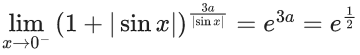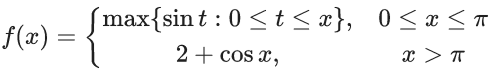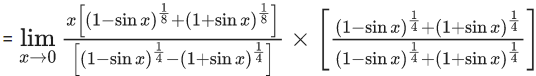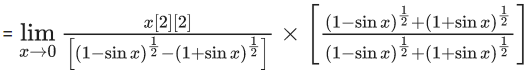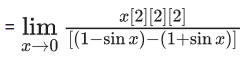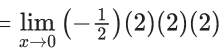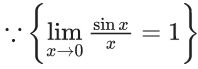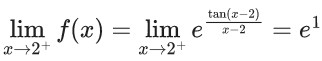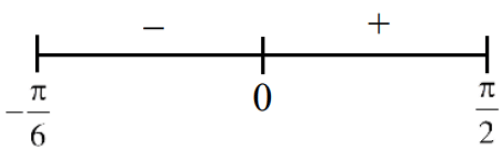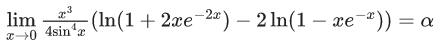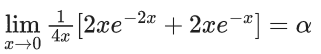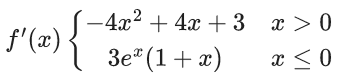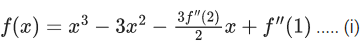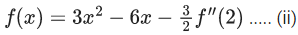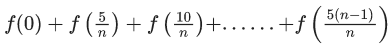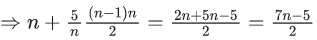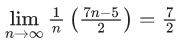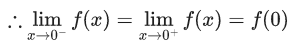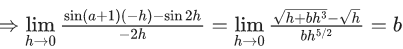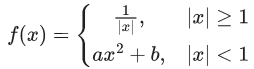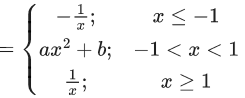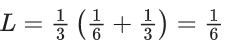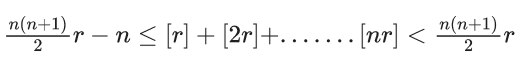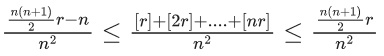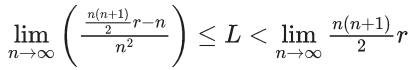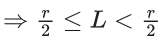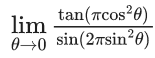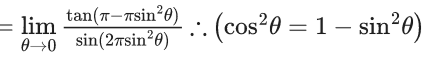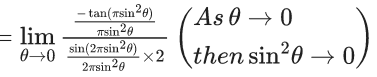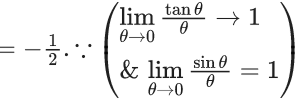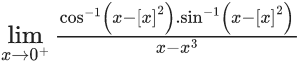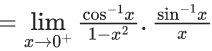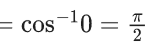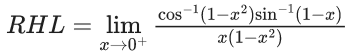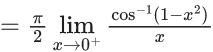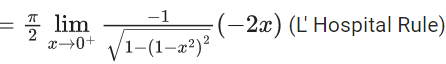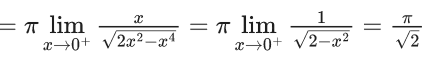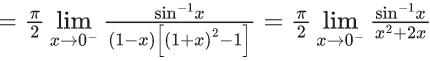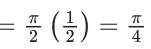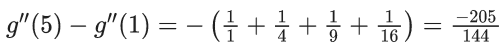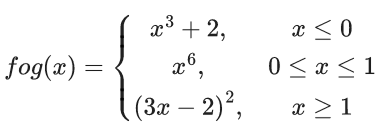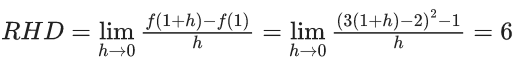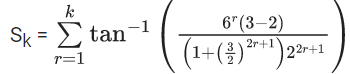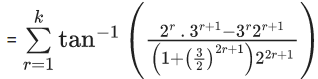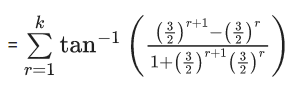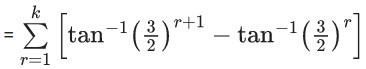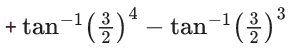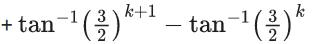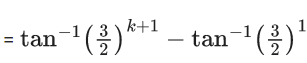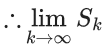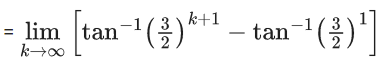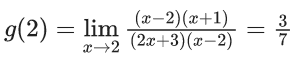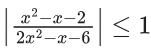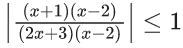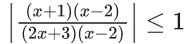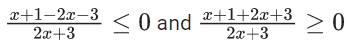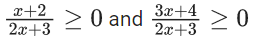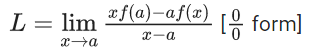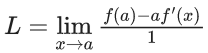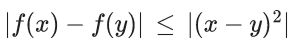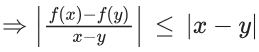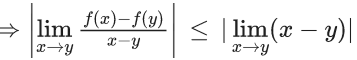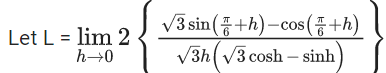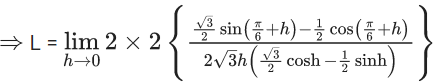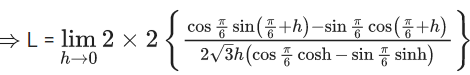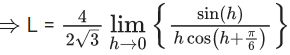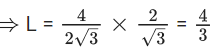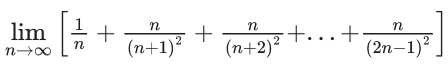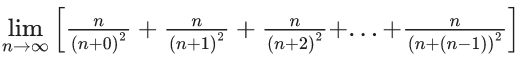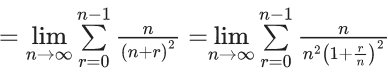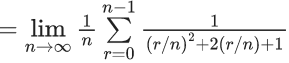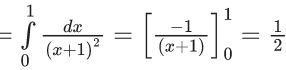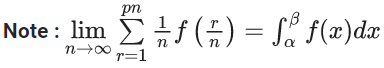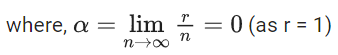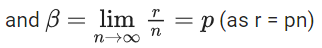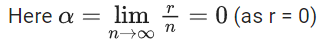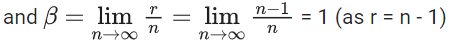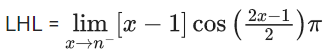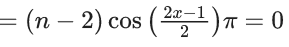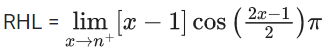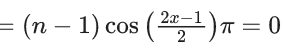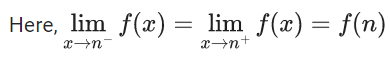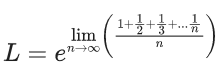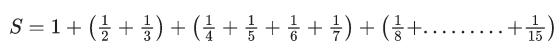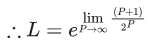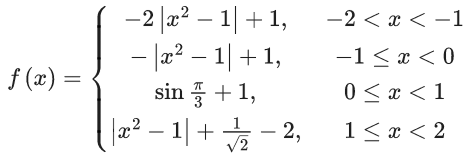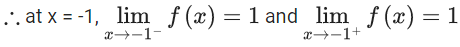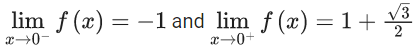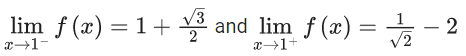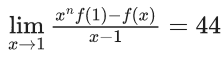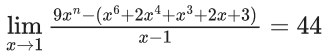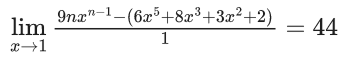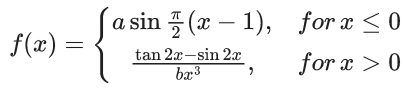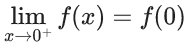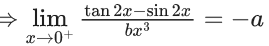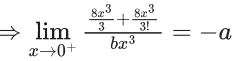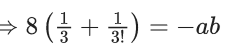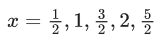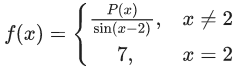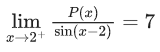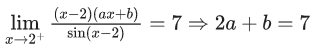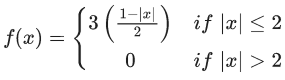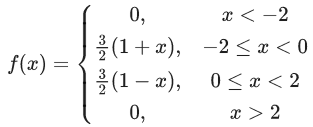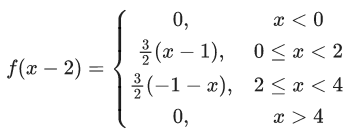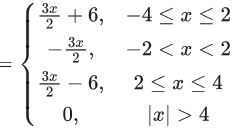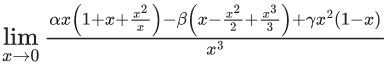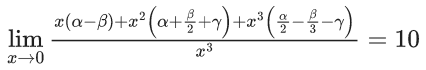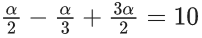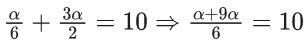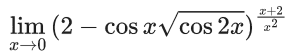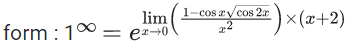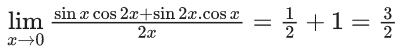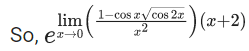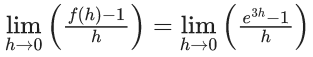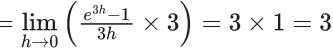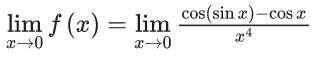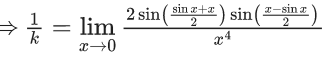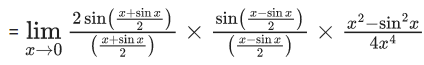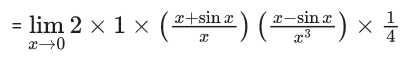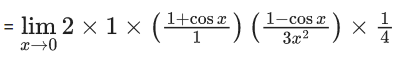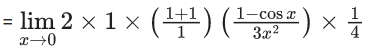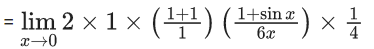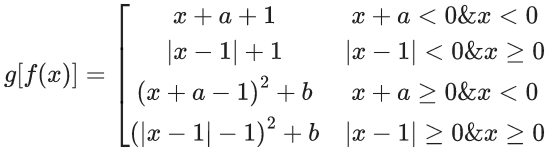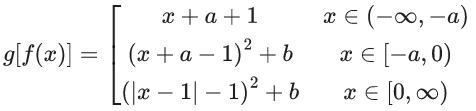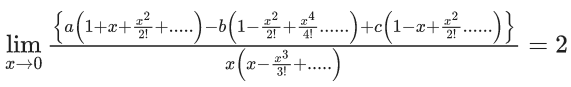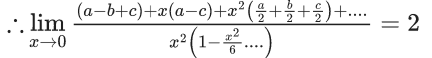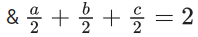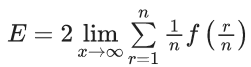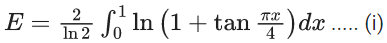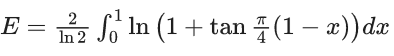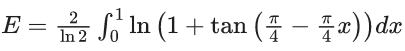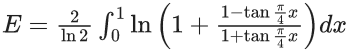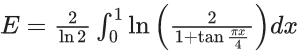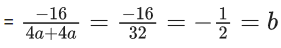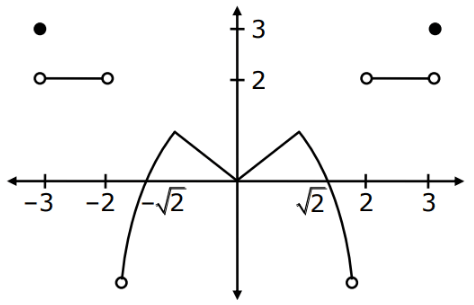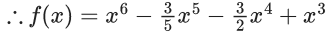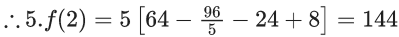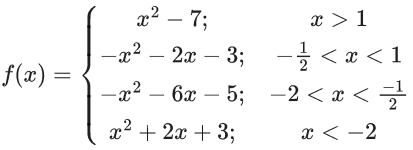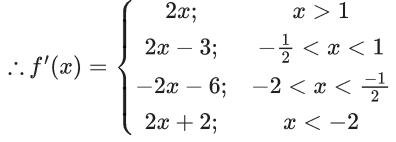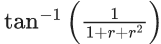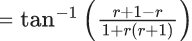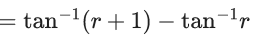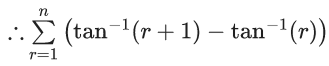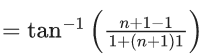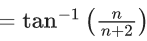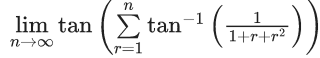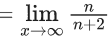JEE Main Previous year questions (2021-23): Limits, Continuity and Differentiability PDF Download

Q.1. 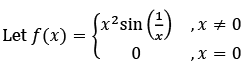      (JEE Main 2023)
Then at x = 0
(a) f is continuous but not differentiable
(b) f and f ′ both are continuous
(c) f ′ is continuous but not differentiable
(d) f is continuous but f ′ is not continuous

Ans. d

Q.2. The set of all values of a for which lim_x→a ([x − 5] − [2x + 2]) = 0 , where [∝] denotes the greatest integer less than or equal to α is equal to   (JEE Main 2023)
(a) [−7.5, −6.5)
(b) [−7.5, −6.5]
(c) (−7.5, −6.5]
(d) (−7.5, −6.5)

Ans. d

Q.3. If, f (x) x³ x²f '(1) xf "(2) f'''(3),  then     (JEE Main 2023)
(a) f(1) + f(2) + f(3) = f(0)
(b) 2f(0) − f(1) + f(3) = f(2)
(c) 3f(1) + f(2) = f(3)
 (d)  f(3) − f(2) = f(1)

Ans. b
f(x) = x³ – x² f'(1) + x f''(2) – f''' (3)
f(x) = x³ – ax² + bx – c
f'(x) = 3x² –2ax + b
f''(x) = 6x –2a
f'''(x) = 6
f'''(3) = 6
f'(1) = 3 – 2a + b = a ⇒ 3a = b + 3
f''(2) = 12 – 2a = b ⇒ 2a = 12 – b
a = 3, b = 6
f'''(3) = 6 = c
f(x) = x³ – 3x² + 6x – 6
f(0) = –6 f(2) = 2
f(1) = –2 f(3) = 12

Q.4. If, then 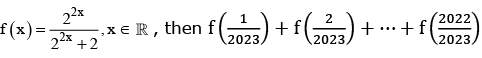 is equal to     (JEE Main 2023)

(a) 1011
(b) 2010
(c) 1010
(d) 2011

Ans. a

Q.5. For positive integer n, define 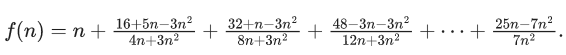 Then, the value of  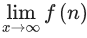is equal to     (JEE Advanced 2022)
(a)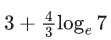
(b)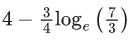
(c)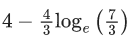
(d)

Ans. b

Q.6. If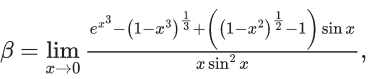 
  then the value of 6β is ___________.     (JEE Advanced 2022)

Ans. 5
Given,

 [Neglecting higher power of x]

Q.7. Let α be a positive real number. Let 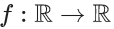 and  be the functions defined by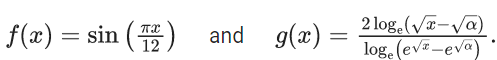
Then the value of 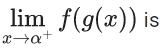      (JEE Advanced 2022)

Ans. 0.49 and 0.51
 [As f(x) is continuous function so we can write this]
Now,





From graph you can see


= (2)/(0+1) = 2

Q.8.  Let the function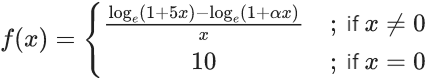
 be continuous at x = 0. Then α is equal to     (JEE Main 2022)
(a) 10
(b) -10
(c) 5
(d) -5

Ans. d
f(x) is continuous at x = 0


= 1 x 5  - α
⇒ α = 5 - 10 = -5

Q.9. The number of points, where the function, f(x) = |x − 1|cos⁡|x − 2|sin⁡|x − 1| + (x − 3)|x² − 5x + 4|, is NOT differentiable, is :     (JEE Main 2022)
(a) 1
(b) 2
(c) 3
(d) 4

Ans. b
f : R → R.
f(x) = |x − 1|cos⁡|x − 2|sin⁡|x − 1| + (x − 3)|x² − 5x + 4|
= |x − 1|cos⁡|x − 2|sin⁡|x − 1| + (x − 3)|x − 1||x − 4|
= |x − 1|[cos⁡|x − 2|sin⁡|x − 1| + (x − 3)|x − 4|]
Sharp edges at x = 1 and x = 4
∴ Non-differentiable at x= 1 and x = 4.

Q.10. If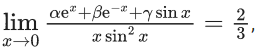 
 where 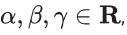 then which of the following is NOT correct?     (JEE Main 2022)
(a) α² + β² + γ² = 6
(b) αβ + βγ + γα + 1 = 0
(c) αβ² + βγ² + γα² + 3 = 0
(d) α² − β² + γ² = 4

Ans. c

⇒ α + β = 0 (to make indeterminant form) ...... (i)
Now,

⇒ α − β + γ = 0 (to make indeterminant form) ...... (ii)
Now,


⇒ α − β + γ = 4 ...... (iii)
⇒ γ = −2
and (i) + (ii)
2α = −γ
⇒ α = 1 and β = −1
and αβ² + βγ² + γα² + 3 =1 − 4 − 2 + 3 = −2

Q.11. The function 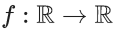 defined by  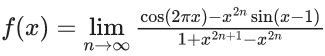is continuous for all x in :      (JEE Main 2022)
(a) R − {−1}
(b)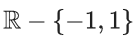
(c) R − {1}
(d) R - {0}

Ans. b

For |x| < 1, f(x) = cos⁡2πx, continuous function



Now,
 so discontinuous at x = 1
 so discontinuous at x = −1
∴ f(x) is continuous for all x ∈ R - {-1, 1}

Q.12. If for p ≠ q ≠ 0, the function 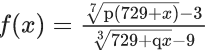 is continuous at x = 0, then :    (JEE Main 2022)
(a) 7pqf(0) − 1 = 0
(b) 63qf(0) − p² = 0
(c) 21qf(0) − p² = 0
(d) 7pqf(0) − 9 = 0

Ans. b

for continuity at
Now,
⇒ p = 3 (To make indeterminant form)



∴ Option (b) is correct.

Q.13. Let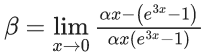 
 for some  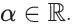Then the value of α + β is :     (JEE Main 2022)
(a) 14/5
(b) 3/2
(c) 5/2
(d) 7/2

Ans. c


So, α = 3 (to make independent form)

Q.14. If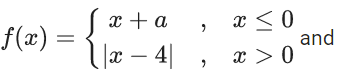 
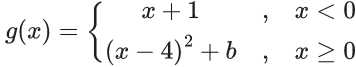  are continuous on R, then (go f)(2) + (fog)(−2) is equal to :     (JEE Main 2022)
(a) -10
(b) 10
(c) 8
(d) -8

Ans. d
 
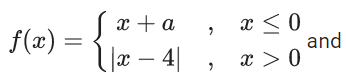
∵ f(x) and g(x) are continuous on R
∴ a = 4 and b = 1 − 16 = −15
then (go f)(2) + (fog)(−2)
= g(2) + f(−1)
= −11 + 3 = −8

Q.15. If the function 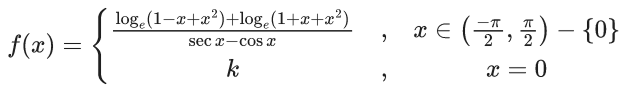 is continuous at x = 0, then k is equal to:     (JEE Main 2022)
(a) 1
(b) -1
(c) e
(d) 0

Ans. a

for continuity at x = 0



= 1

Q.16. 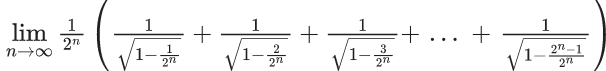 is equal to     (JEE Main 2022)
(a) 1/2
(b) 1
(c) 2
(d) -2

Ans. c

Let 2n = t and if n → ∞ then t → ∞

Q.17. 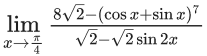 is equal to     (JEE Main 2022)
(a) 14
(b) 7
(c) 14√2
(d) 7√2

Ans. a

Q.18. If  then 8(α + β) is equal to :     (JEE Main 2022)
(a) 4
(b) -8
(c) -4
(d) 8

Ans. c

[This limit will be zero when α < 0 as when α > 0 then overall limit will be ∞.]


Here power of "n" in the numerator is 2 and power of "n" in the denominator is 1.
To get the value of limit equal to zero power of "n" should be equal in both numerator and denominator, otherwise value of limit will be infinite (∞).
∴ Coefficient of n2 should be 0 in this case.
∴ 1 − α² = 0
⇒ α =±1
But α should be < 0
∴ α = +1 not possible
∴ α = −1.

Divide numerator and denominator by n then we get,



∴ 8(α + β)

= 8 x -(1/2)
= -4

Q.19. 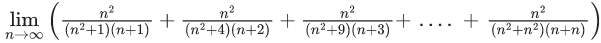 is equal to :     (JEE Main 2022)
(a)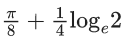
(b)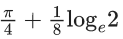
(c)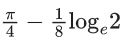
(d)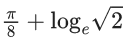

Ans. a

Q.20. Let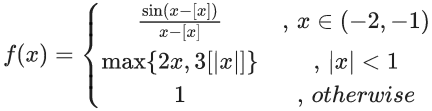
 where [t] denotes greatest integer ≤ t. If m is the number of points where f is not continuous and n is the number of points where f is not differentiable, then the ordered pair (m, n) is :     (JEE Main 2022)
(a) (3, 3)
(b) (2, 4)
(c) (2, 3)
(d) (3, 4)

Ans. c


It clearly shows that f(x) is discontinuous
At x = −1, 1 also non differentiable
and at x = 0,

∴ f(x) is not differentiable at x = 0
∴ m = 2, n = 3

Q.21. 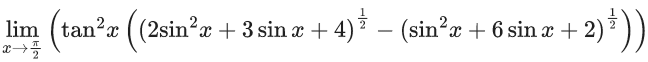 is equal to    (JEE Main 2022)
(a) 1/12
(b) -(1/18)
(c) -(1/12)
(d) 1/6

Ans. a



= 1/12

Q.22. Let f(x) = min {1, 1 + x sin x}, 0 ≤ x ≤ 2π. If m is the number of points, where f is not differentiable and n is the number of points, where f is not continuous, then the ordered pair (m, n) is equal to     (JEE Main 2022)
(a) (2, 0)
(b) (1, 0)
(c) (1, 1)
(d) (2, 1)

Ans. b
f(x) = min{1, 1 + xsin⁡x}, 0 ≤ x ≤ x

Now at
∴ f(x) is continuous in [0, 2π]
Now, at x = π

∴ f(x) is not differentiable at x = π
∴ (m, n) = (1, 0)

Q.23. 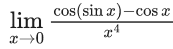 is equal to :     (JEE Main 2022)
(a) 1/3
(b) 1/4
(c) 1/6
(d) 1/12

Ans. c




= 1/6

Q.24. Let f, g : R → R be two real valued functions defined as 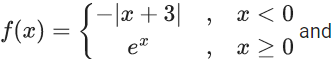 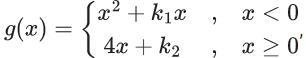 where k₁ and k₂ are real constants. If (gof) is differentiable at x = 0, then (gof) (− 4) + (gof) (4) is equal to     (JEE Main 2022)
(a) 4(e⁴+1)
(b) 2(2e⁴+1)
(c) 4e⁴
(d) 2(2e⁴−1)

Ans. d
∵ gof is differentiable at x = 0
So R.H.D = L.H.D

⇒ 4 = 6 − k₁ ⇒ k₁ = 2
Also f(f(0⁺)) = g(f(0⁻))
⇒ 4 + k₂ = 9 − 3k₁ ⇒ k₂ = −1
Now g(f(−4)) + g(f(4))
= g(−1) + g(e⁴) = (1 − k₁) + (4e⁴ + k₂)
= 4e⁴ − 2
= 2(2e⁴ − 1)

Q.25. 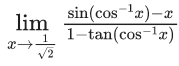 is equal to :    (JEE Main 2022)
(a) √2
(b) -√2
(c) 1/√2
(d) -(1/√2)

Ans. d

Let cos − 1x = t
⇒ x = cos⁡t
When  then

Q.26. Let a be an integer such that 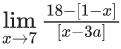 exists, where [t] is greatest integer ≤ t. Then a is equal to :     (JEE Main 2022)
(a) -6
(b) -2
(c) 2
(d) 6

Ans. a



For limit to exist
LHL = RHL


∴ a = -6

Q.27. Let f : R → R be defined as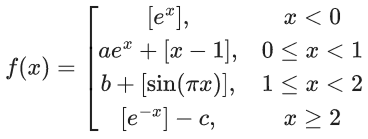 

where a, b, c ∈ R and [t] denotes greatest integer less than or equal to t. Then, which of the following statements is true?    (JEE Main 2022)
(a) There exists a, b, c ∈ R such that f is continuous on R.
(b) If f is discontinuous at exactly one point, then a + b + c = 1
(c) If f is discontinuous at exactly one point, then a + b + c ≠ 1
(d) f is discontinuous at at least two points, for any values of a, b and c

Ans. c

To be continuous at x = 0
a − 1 = 0
to be continuous at x = 1
ae − 1 = b = b − 1 ⇒ not possible
to be continuous at x = 2
b − 1 = − c ⇒ b + c = 1
If a = 1 and b + c = 1 then f(x) is discontinuous at exactly one point.

Q.28. The value of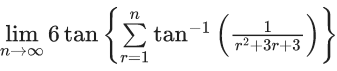
 is equal to :     (JEE Main 2022)
(a) 1
(b) 2
(c) 3
(d) 6

Ans. c


= 3

Q.29. Let f, g : R → R be functions defined by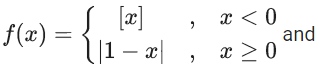 
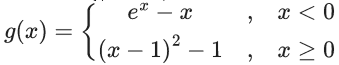 where [x] denote the greatest integer less than or equal to x. Then, the function fog is discontinuous at exactly :    (JEE Main 2022)
(a) one point
(b) two points
(c) three points
(d) four points

Ans. b

Q.30. The value of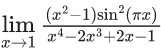 
 is equal to:    (JEE Main 2022)
(a) π²/6
(b) π²/3
(c) π²/2
(d) π²

Ans. d

Let x = 1 + h
∴ when x → 1 then h → 0

= π² x 1
= π²

Q.31. If [t] denotes the greatest integer ≤t, then the number of points, at which the function f(x) = 4|2x + 3| + 9[x + (1/2)] − 12[x + 20] is not differentiable in the open interval (−20, 20), is __________.    (JEE Main 2022)

Ans. 79
f(x)= 4|2x + 3| + 9[x + 12] − 12[x + 20]
= 4|2x + 3| + 9[x + (1/2)] − 12[x] −240
f(x) is non differentiable at x = −(3/2)
and f(x) is discontinuous at {−19, −18 ,…., 18, 19}
as well as
at same point they are also non differentiable.
∴ Total number of points of non differentiability = 39 + 40 = 79

Q.32. 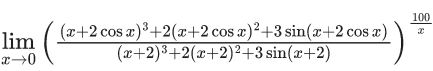 is equal to _____.     (JEE Main 2022)

Ans. 1
Let x + 2cos⁡x = a
x + 2 = b
as x → 0, a → 2 and b → 2



= e°
= 1

Q.33. If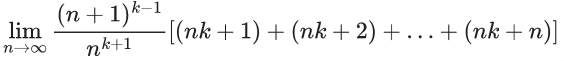 
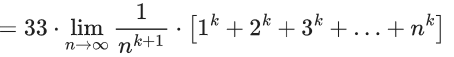  then the integral value of k is equal to _____.     (JEE Main 2022)

Ans. 5

Q.34. Suppose 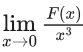 exists and is equal to L, where
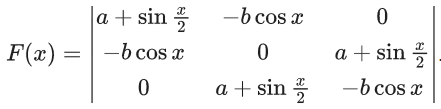 Then, −112 L is equal to _____.     (JEE Main 2022)

Ans. 14
Given,



Now,


Given limit exists, it only possible when a = 0 and b = 0.



∴ −112L = −112 × −(1/8) = 14

Q.35. Let f(x) =[ 2x² + 1] and g(x) =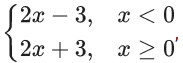
 where [t] is the greatest integer ≤ t. Then, in the open interval (−1, 1), the number of points where fog is discontinuous is equal to ____.    (JEE Main 2022)

Ans. 62

Q.36. If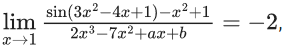
 then the value of (a − b) is equal to _____.    (JEE Main 2022)

Ans. 11

Q.37. Let f : R → R be defined by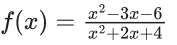
Then which of the following statements is (are) TRUE?     (JEE Advanced 2021)
(a) f is decreasing in the interval (−2, −1)
(b) f is increasing in the interval (1, 2)
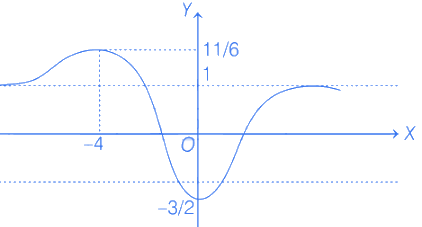
(c) f is onto
(d) Range of f is [−(3/2),2]

Ans. a and b
Given,

Sign scheme for f'(x)
Here, f is decreasing in the interval (−2, −1) and f is increasing in the interval (1, 2).
Now, f(−4) = 11/6,f(0) = (−3)/2 [from Eq. (i)]
and

Hence, f(x) is into.

f(x) has local maxima at x = −4
and local minima at x = 0.

Q.38. Let f be any continuous function on [0, 2] and twice differentiable on (0, 2). If f(0) = 0, f(1) = 1 and f(2) = 2, then    (JEE Main 2021)
(a) f''(x) = 0 for all x ∈ (0, 2)
(b) f''(x) = 0 for some x ∈ (0, 2)
(c) f'(x) = 0 for some x ∈ [0, 2]
(d) f''(x) > 0 for all x ∈ (0, 2)

Ans. b
f(0) = 0, f(1) = 1 and f(2) = 2
Let h(x) = f(x) − x
Clearly h(x) is continuous and twice differentiable on (0, 2)
Also, h(0) = h(1) = h(2) = 0
∴ h(x) satisfies all the condition of Rolle's theorem.
∴ there exist C₁ ∈(0, 1) such that h'(c₁) = 0
⇒ f'(₁) − 1 = 0 ⇒ f'(c₁) = 1
also there exist c₂ ∈(1, 2) such that h'(c₂) = 0
⇒ f'(c₂) = 1
Now, using Rolle's theorem on [c₁, c₂] for f'(x)
We have f''(c) = 0, c ∈ (c₁, c₂)
Hence, f''(x) = 0 for some x ∈ (0, 2).

Q.39. If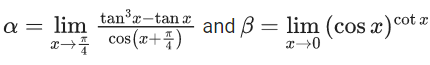 
 are the roots of the equation, ax² + bx − 4 = 0, then the ordered pair (a, b) is :     (JEE Main 2021)
(a) (1, -3)
(b) (-1, 3)
(c) (-1, -3)
(d) (1, 3)

Ans. d

Using L Hospital rule

α = −4



α = −4; β = 1
If ax² + bx − 4 = 0 are the roots then
16a − 4b − 4 = 0 & a + b − 4 = 0
⇒ a = 1 & b = 3

Q.40. 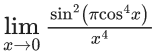 is equal to :     (JEE Main 2021)
(a) π²
(b) 2π²
(c) 4π²
(d) 4π

Ans. c

Q.41. If the function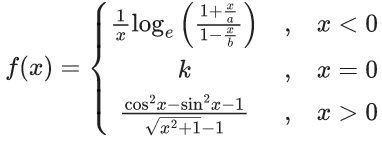
 is continuous at x = 0, then  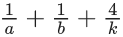is equal to :      (JEE Main 2021)
(a) -5
(b) 5
(c) -4
(d) 4

Ans. a
If f(x) is continuous at x = 0, RHL = LHL = f(0)

Q.42. The function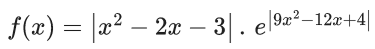 is not differentiable at exactly :     (JEE Main 2021)
(a) four points
(b) three points
(c) two points
(d) one point

Ans. c


Clearly, non-differentiable at x = −1 & x = 3.

Q.43. If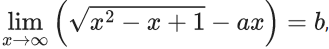 
 then the ordered pair (a, b) is :     (JEE Main 2021)
(a) (1, (1/2))
(b) (1, -(1/2))
(c) (-1, (1/2))
(d) (-1, -(1/2))

Ans. b




⇒ 1 − a² = 0 ⇒ a = 1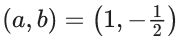


 

Q.44. If α, β are the distinct roots of x² + bx + c = 0, then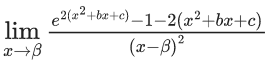 
 is equal to :     (JEE Main 2021)
(a) b² + 4c
(b) 2(b² + 4c)
(c) 2(b² − 4c)
(d) b² − 4c

Ans. c




= 2(β − α)² = 2(b² − 4c)

Q.45. 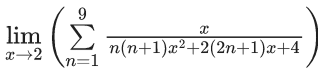 is equal to :     (JEE Main 2021)
(a) 9/44
(b) 5/24
(c) 1/5
(d) 7/36

Ans. a

Q.46. The value of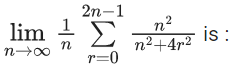 
     (JEE Main 2021)
(a) (1/2) tan^-1(2)
(b) (1/2) tan^-1(4)
(c) tan^-1(4)
(d) (1/4) tan^-1(4)

Ans. b

Q.47. Let f : R → R be a function such that f(2) = 4 and f'(2) = 1. Then, the value of 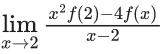 is equal to :     (JEE Main 2021)
(a) 4
(b) 8
(c) 16
(d) 12

Ans. d
Apply L' Hospital Rule

Q.48. Let 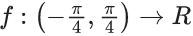 be defined as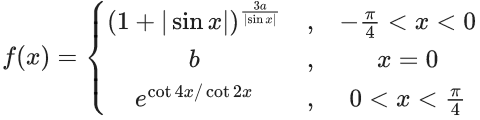

If f is continuous at x = 0, then the value of 6a + b² is equal to :     (JEE Main 2021)
(a) 1 - e
(b) e - 1
(c) 1 + e
(d) e

Ans. c



a = 1/6 ⇒ 6a = 1
∴ (6a + b²) = (1 + e)

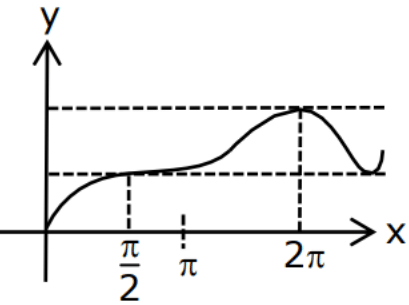
Q.49. Let f : [0, ∞) → [0, 3] be a function defined by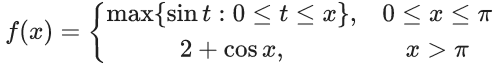
Then which of the following is true?    (JEE Main 2021)
(a) f is continuous everywhere but not differentiable exactly at one point in (0, ∞)
(b) f is differentiable everywhere in (0, ∞)
(c) f is not continuous exactly at two points in (0, ∞)
(d) f is continuous everywhere but not differentiable exactly at two points in (0, ∞)

Ans. b

Graph of max{sin⁡ t : 0 ≤ t ≤ x} in x ∈ [0, π]

& graph of cos x for x ∈ [π, ∞)

So graph of


f(x) is differentiable everywhere in (0, ∞)

Q.50. The value of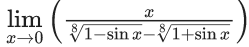
 is equal to :    (JEE Main 2021)
(a) 0
(b) 4
(c) -4
(d) -1

Ans. c






= -4

Q.51. Let f : R → R be defined as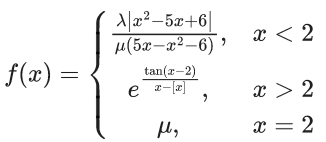

where [x] is the greatest integer lss than or equal to x. If f is continuous at x = 2, then λ + μ is equal to      (JEE Main 2021)
(a) e(−e + 1)
(b) e(e − 2)
(c) 1
(d) 2e − 1

Ans. a


For continuity μ = e = −(λ/μ) ⇒ μ = e, λ = −e²
λ + μ = e(−e + 1)

Q.52. Let f(x) = 3sin⁴x + 10sin³x + 6sin²x − 3, x ∈[−(π/6), (π/2)]. Then, f is :     (JEE Main 2021)
(a) increasing in (−(π/6), (π/2))
(b) decreasing in (0, (π/2))
(c) increasing in (−(π/6), 0)
(d) decreasing in (−(π/6), 0)

Ans. d
f(x) = 3sin⁴x + 10sin³x + 6sin²x − 3, x ∈ [−(π/6), (π/2)]
f′(x) = 12sin³xcos⁡x + 30sin²xcos⁡x + 12sin⁡xcos⁡x
= 6sin⁡xcos⁡x(2sin²x + 5sin⁡x + 2)
= 6sin⁡xcos⁡x(2sin⁡x + 1)(sin + 2)

Decreasing in (−(π/6), 0)

Q.53. Let f : R → R be defined as f(x) =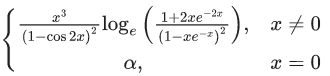
 If f is continuous at x = 0, then α is equal to :     (JEE Main 2021)
(a) 1
(b) 3
(c) 0
(d) 2

Ans. a
For continuity


= (1/4)(4) = α = 1

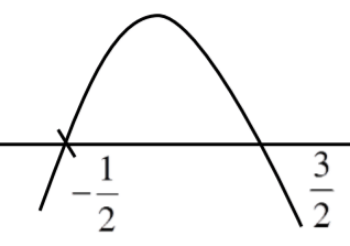
Q.54. Let f : R → R be defined as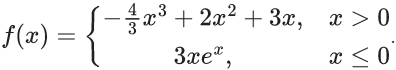
 Then f is increasing function in the interval     (JEE Main 2021)
(a) ((-1/2), 2)
(b) (0, 2)
(c) (-1, (3/2))
(d) (-3, -1)

Ans. c


For x > 0, f′(x) = −4x² + 4x + 3
f(x) is increasing in ((−1/2), (3/2))
For x ≤ 0, f'(x) = 3e^x(1 + x)
f'(x) > 0 ∀ x ∈(−1, 0)
⇒ f(x) is increasing in (−1, 0)
So, in complete domain, f(x) is increasing in (−1, (3/2))

Q.55. The sum of all the local minimum values of the twice differentiable function f : R → R defined by 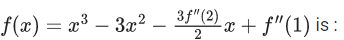     (JEE Main 2021)
(a) -22
(b) 5
(c) -27
(d) 0

Ans. c


f″(x) = 6x − 6 ..... (iii)
Now, is 3^rd equation
f″(2) = 12 − 6 = 6
f″(11 = 0)
Use (ii)
f′(x) = 3x² −6x − (3/2)f″(2)
f′(x) = 3x² − 6x − (3/2) ×6
f′(x) = 3x² − 6x − 9
f′(x) = 0
3x2−6x−9=0
⇒ x = −1 & 3
Use (iii)
f″(x) = 6x − 6
f″(−1) = −12 < 0 maxima
f″(3) = 12 > 0 minima.
Use (i)
f(x) = x³ − 3x² − (3/2)f″(2)x + f″(1)
f(x) = x³ − 3x² − (3/2) × 6 × x + 0
f(x) = x³ − 3x² − 9x
f(3) = 27 − 27 − 9 × 3 = −27

Q.56. If f : R → R is given by f(x) = x + 1, then the value of  is :     (JEE Main 2021)
(a) 3/2
(b) 5/2
(c) 1/2
(d) 7/2

Ans. d

 

Q.57. Let a function f : R → R be defined as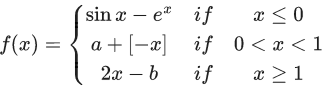  

where [ x ] is the greatest integer less than or equal to x. If f is continuous on R, then (a + b) is equal to:     (JEE Main 2021)
(a) 4
(b) 3
(c) 2
(d) 5

Ans. b
Continuous x = 0
f(0⁺) = f(0⁻) ⇒ a − 1 = 0 − e⁰
⇒ a = 0
Continuous at x = 1
f(1⁺) = f(1⁻)
⇒ 2(1) − b = a + (−1)
⇒ b = 2 − a + 1 ⇒ b = 3
∴ a + b = 3

Q.58. Let f : R → R be a function defined as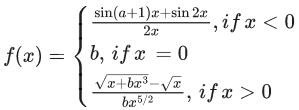

If f is continuous at x = 0, then the value of a + b is equal to :    (JEE Main 2021)
(a) -3
(b) -2
(c) -(5/2)
(d) -(3/2)

Ans. c
∵ f(x) is continuous at x = 0




⇒ a = −3, b = (1/2)
∴ a + b = −3 + (1/2) = −(5/2)

Q.59. If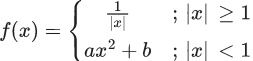
 is differentiable at every point of the domain, then the values of a and b are respectively :      (JEE Main 2021)
(a) 1/2, 1/2
(b) 1/2, -(3/2)
(c) 5/2, -(3/2)
(d) -(1/2), (3/2)

Ans. d


As f(x) is differentiable so it is also continuous,
at x = 1,

⇒ a + b = 11
⇒ a + b = 1 ...... (1)
As f(x) is differentiable, so at x = 1
L.H.D. = R.H.D.
⇒ 2ax= −1/x²
⇒ 2a= −1
⇒ a= −(1/2)
From (1), b = 3/2

Q.60. If 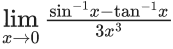 is equal to L, then the value of (6L + 1) is    (JEE Main 2021)
(a) 1/6
(b) 1/2
(c) 6
(d) 2

Ans. d


∴ 6L + 1 = 6.(1/6) + 1 = 2

Q.61. The value of 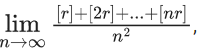 where r is a non-zero real number and [r] denotes the greatest integer less than or equal to r, is equal to :     (JEE Main 2021)
(a) r
(b) r/2
(c) 0
(d) 2r

Ans. b
We know,
(x − 1) ≤ [x] < x
∴ (r − 1) ≤ [r] < r
(2r − 1) ≤ [2r] < 2r
.
.
.
(nr − 1) ≤ [nr] < nr
Adding

⇒ L = r/2

Q.62. The value of the limit 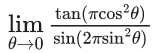 is equal to :    (JEE Main 2021)
(a) 0
(b) -(1/2)
(c) 1/4
(d) -(1/4)

Ans. b
Given,

Q.63. The value of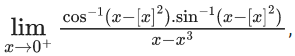

where [x] denotes the greatest integer ≤ x is :    (JEE Main 2021)
(a) π
(b) π/4
(c) π/2
(d) 0

Ans. c

Q.64. Let α ∈ R be such that the function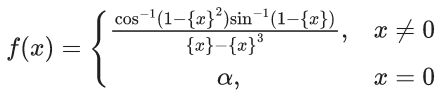

is continuous at x = 0, where {x} = x − [ x ] is the greatest integer less than or equal to x. Then :     (JEE Main 2021)
(a) no such α exists
(b) α = 0
(c) α = π/4
(d) α = π/√2

Ans. a







As LHL ≠ RHL so f(x) is not continuous at x = 0

Q.65. Let f : S → S where S = (0, ∞) be a twice differentiable function such that f(x + 1) = xf(x). If g : S → R be defined as g(x) = log_e f(x), then the value of |g''(5) − g''(1)| is equal to :     (JEE Main 2021)
(a) 1
(b) 187/144
(c) 197/144
(d) 205/144

Ans. d
f(x + 1) = xf(x)
ln⁡(f(x + 1)) = ln⁡x + ln⁡f(x)
g(x + 1) = ln⁡x + g(x)
g(x + 1)−g(x) = ln⁡x ..... (i)
g′(x + 1)−g′(x) = 1/x
g″(x + 1)−g″(x) = −1/(x²)
g″(2)−g′(1) = −1/1 .... (ii)
g″(3)−g″(2) = −1/4 .... (iii)
g″(4)−g″(3) = −1/9 ..... (iv)
g″(5)−g″(4) = −1/16 ....(v)
Adding (ii), (iii), (iv) & (v)

|g″(5) − g″(1)| = (205/144)

Q.66. Let the functions f : R → R and g : R → R be defined as :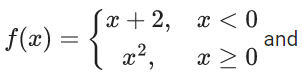
 
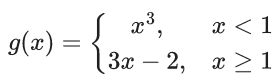
Then, the number of points in R where (fog) (x) is NOT differentiable is equal to :    (JEE Main 2021)
(a) 0
(b) 3
(c) 1
(d) 2

Ans. c

∵ fog(x) is discontinuous at x = 0 then non-differentiable at x = 0
Now,
at x = 1


Number of points of non-differentiability = 1

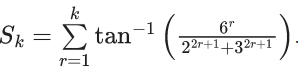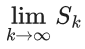Q.67. Let  Then  is equal to :    (JEE Main 2021)
(a) cot^-1(3/2)
(b) π/2
(c) tan^-1 (3)
(d) tan^-1 (3/2)

Ans. a




  
.
.
.




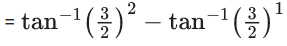
= tan⁻¹(∞)−tan⁻¹(3/2)
= π/2 − tan⁻¹(3/2)
= cot⁻¹(3/2)

Q.68. Let f : R → R be defined as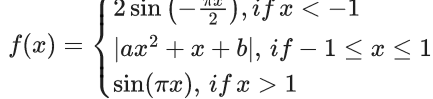

If f(x) is continuous on R, then a + b equals :     (JEE Main 2021)
(a) -3
(b) 3
(c) -1
(d) 1

Ans. c
f(−1⁻) = 2
f(−1⁺ )= |a + b − 1|
|a + b − 1| = 2 ... (i)
f(1⁻) = |a + b + 1|
f(1⁺) = 0
|a + b + 1| = 0 ⇒ a + b + 1 = 0
⇒ a + b = −1 .... (ii)

Q.69. Let f(x) = sin⁻¹x and g(x) = 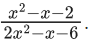 If g(2) =  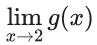, then the domain of the function fog is :     (JEE Main 2021)
(a) (−∞,−2] ∪ [−4/3, ∞)
(b) (−∞,−2] ∪ [−1, ∞)
(c) (−∞,−2] ∪ [−(3/2), ∞)
(d) (−∞,−1] ∪ [2, ∞)

Ans. a

Domain of fog(x) = sin⁻¹(g(x))
⇒ |g(x)| ≤ 1






x ∈ (−∞,−2] ∪ [−(4/3), ∞)

Q.70. Let f(x) be a differentiable function at x = a with f'(a) = 2 and f(a) = 4.
Then 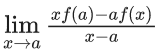 equals :    (JEE Main 2021)
(a) 4 - 2a
(b) 2a + 4
(c) a +4
(d) 2a - 4

Ans. a

Using L' Hospital rule we get

f(a) − af′(a) = 4 − 2a

Q.71. Let f be any function defined on R and let it satisfy the condition : |f(x)−f(y)| ≤ |(x−y)²|, ∀(x, y) ∈ R. If f(0) = 1, then :    (JEE Main 2021)
(a) f(x) can take any value in R
(b) f(x) < 0, ∀_x ∈R
(c) f(x) > 0, ∀_x ∈ R
(d) f(x) = 0, ∀_x ∈ R

Ans. c



⇒ |f′(x)| ≤ 0
⇒ f′(x) = 0
⇒ f(x) is constant function.
∵ f(0) = 1 then f(x) = 1

Q.72. The value of 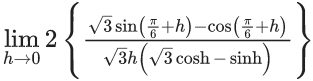 is :       (JEE Main 2021)
(a) 4/3
(b) 2/3
(c) 3/4
(d) 2/√3

Ans. a

Q.73. 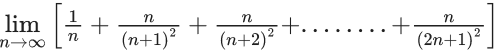 is equal to :    (JEE Main 2021)
(a) 1/2
(b) 1/3
(c) 1
(d) 1/4

Ans. a

Q.74. If f : R → R is a function defined by f(x)= [x - 1] 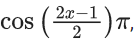 where [.] denotes the greatest integer function, then f is :    (JEE Main 2021)
(a) continuous for every real x
(b) discontinuous at all integral values of x except at x = 1
(c) discontinuous only at x = 1
(d) continuous only at x = 1

Ans. a
Given,  where [.] is greatest integer function and f : R → R
∵ It is a greatest integer function then we need to check its continuity at x ∈ I except these it is continuous.
Let, x = n where n ∈ I
Then




and f(n) = 0

∴ It is continuous at every integers.
Therefore, the given function is continuous for all real x.

Q.75. 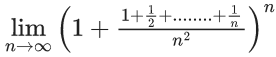 is equal to :    (JEE Main 2021)
(a) 1/2
(b) 1
(c) 0
(d) 1/e

Ans. b
It is 1^∞ form



S<1+1+1+1+.......+1
S<P+1

⇒ L = e° = 1.

Q.76. Let [t] denote the greatest integer ≤ t. The number of points where the function f(x) = [x]|x²−1| + sin⁡(π/([x]+3)) − [x + 1], x ∈ (−2, 2) is not continuous is ____.     (JEE Main 2021)

Ans. 2
f(x) = [x]|x²−1| + sin⁡(π/([x]+3)) − [x + 1]


Hence continuous at x = –1
Similarly check at x = 0,

So, f(x) discontinuous and at x = 0

So, f(x) discontinuous and at x = 1
Hence 2 points of discontinuity.

Q.77. Let f(x)=x⁶ + 2x⁴ + x³ + 2x + 3, x ∈ R. Then the natural number n for which  is _______.     (JEE Main 2021)

Ans. 7
f(x) = x⁶ + 2x⁴ + x³ + 2x + 3



⇒ 9n − (19) = 44
⇒ 9n = 63
⇒ n = 7

Q.78. Let a, b ∈ R, b ∈ 0, Define a function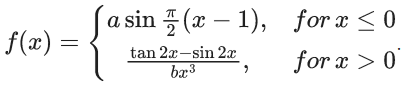

If f is continuous at x = 0, then 10 − ab is equal to ____.     (JEE Main 2021)

Ans. 14

For continuity at '0'




⇒ 4 = −ab
⇒ 10 − ab = 14

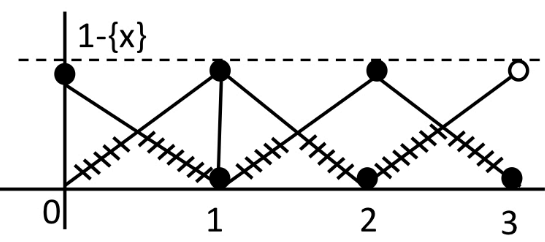
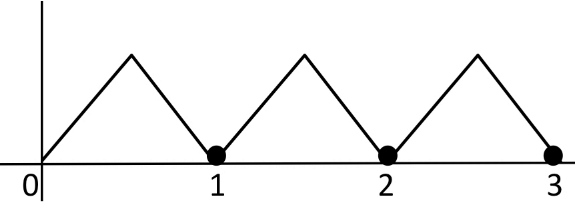
Q.79. Let f:[0, 3] → R be defined by f(x) = min{x − [x], 1 + [x] − x} where [x] is the greatest integer less than or equal to x. Let P denote the set containing all x ∈ [0, 3] where f i discontinuous, and Q denote the set containing all x ∈ (0, 3) where f is not differentiable. Then the sum of number of elements in P and Q is equal to    (JEE Main 2021)

Ans. 5

1 − {x} = 1 − x; 0 ≤ x < 1

Non differentiable at

Q.80. Consider the function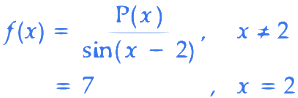

where P(x) is a polynomial such that P'' (x) is always a constant and P(3) = 9. If f(x) is continuous at x = 2, then P(5) is equal to ____.     (JEE Main 2021)

Ans. 39

P''(x) = const. ⇒ P(x) is a 2 degree polynomial
f(x) is cont. at x = 2
f(2⁺) = f(2⁻)


P(x) = (x − 2)(ax + b)
P(3) = (3 − 2)(3a + b) = 9 ⇒ 3a + b = 9
a = 2, b = 3
P(5) = (5 − 2)(2.5 + 3) = 3.13 = 39

Q.81. Let f : R → R be a function defined as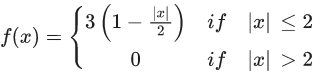
 Let g : R → R be given by g(x) = f(x + 2) −f(x − 2). If n and m denote the number of points in R where g is not continuous and not differentiable, respectively, then n + m is equal to _____.    (JEE Main 2021)

Ans. 4

g(x) = f(x+2) − f(x−2)



g(x) = f(x+2) + f(x−2)

So, n = 0 and m = 4
∴ m + n = 4

Q.82. If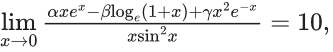
,α, β, γ ∈ R, then the value of α + β + γ is ______.     (JEE Main 2021)

Ans. 3


For limit to exist

β = α, γ = −3(α/2)
Put in (i)


⇒ α = 6
α = 6, β = 6, γ = −9
α + β + γ = 3

Q.83. Let a function g : [ 0, 4 ] → R be defined as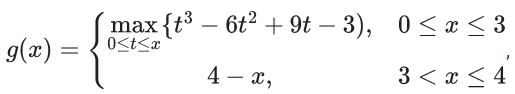

then the number of points in the interval (0, 4) where g(x) is NOT differentiable, is ______.     (JEE Main 2021)

Ans. 1
f(x) = x³ − 6x² + 9x − 3
f(x) = 3x² − 12x + 9 = 3(x−1)(x−3)
f(1) = 1, f(3) = 3

g(x) is continuous

g(x) is non-differentiable at x = 3

Q.84. If the value of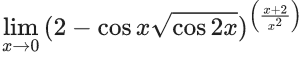

is equal to e^a, then a is equal to _____.     (JEE Main 2021)

Ans. 3


Now,
 (by L' Hospital Rule)


= e^{(3/2) × 2} = e³
⇒ a = 3

Q.85. Let f : R → R satisfy the equation f(x + y) = f(x) . f(y) for all x, y ∈ R and f(x) ≠ 0 for any x ∈ R. If the function f is differentiable at x = 0 and f'(0) = 3, then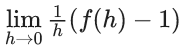is equal to ______.     (JEE Main 2021)

Ans. 3
Given, f(x+y) = f(x).f(y) ∀ x, y ∈ R
∴ f(x) = a^x ⇒ f′(x) = a^x.log⁡(a)
Now, f′(0) = log⁡(a) ⇒ 3 = log⁡(a) ⇒ a = e³
∴ f(x) = (e³)^x = e^3x
∴ f(h) = e^3h
Now,

Q.86. If the function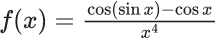
 is continuous at each point in its domain and f(0) = (1/k), then k is ______.      (JEE Main 2021)

Ans. 6

Q.87. Let f : R → R and g : R → R be defined as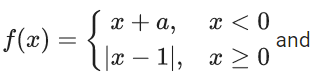
 
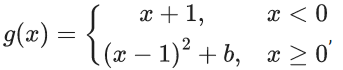
where a, b are non-negative real numbers. If (gof) (x) is continuous for all x ∈ R, then a + b is equal to ____.     (JEE Main 2021)

Ans. 1




g(f(x)) is continuous.
At x = −a
-a + a + 1 = (-a + a - 1)² + b
⇒ 1 = b + 1
⇒ b = 0
at x = 0
(a −1)² + b = (|0 - 1| - 1)² + b
⇒ (a −1)² + b = b
⇒ a = 1
⇒ a + b = 1

Q.88. If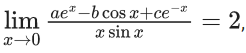
 then a + b + c is equal to ____.     (JEE Main 2021)

Ans. 4


For this limit to exist
a − b + c = 0 & a − c = 0

⇒ a + b + c = 4

Q.89. Let f : (0, 2) → R be defined as f(x) = log₂ 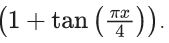 Then, 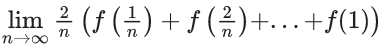 is equal to ____.     (JEE Main 2021)

Ans. 1


replacing x → 1 − x





equation (i) + (ii)
2E = 2 ⇒ E = 1

Q.90. If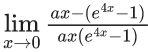
 exists and is equal to b, then the value of a − 2b is ___.     (JEE Main 2021)

Ans. 5

Applying L' Hospital Rule

This is ((a−4)/0).
limit exist only when a−4=0 ⇒ a = 4
Applying L' Hospital Rule


a−2b = 4−2((−1)/2) = 4 + 1 = 5

Q.91. A function f is defined on [−3, 3] as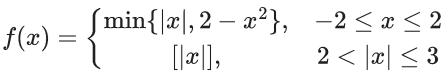
 where [x] denotes the greatest integer ≤ x. The number of points, where f is not differentiable in (−3, 3) is  ____.     (JEE Main 2021)

Ans. 5

Points of non-differentiability in (−3, 3) are at x = −2, −1, 0, 1, 2.
i.e. 5 points.

Q.92. Let f(x) be a polynomial of degree 6 in x, in which the coefficient of x⁶ is unity and it has extrema at x = −1 and x = 1. If 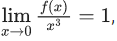 then 5.f(2) is equal to     (JEE Main 2021)

Ans. 144
f(x) = x⁶ + ax⁵ + bx⁴ + x³
∴ f′(x) = 6x⁵ + 5ax⁴ + 4bx³ + 3x²
Roots 1 & −1
∴ 6 + 5z + 4b + 3 = 0 & −6 + 5a − 4b + 3 = 0 solving
a = −(3/5)
b = −(3/2)

Q.93. The number of points, at which the function f(x) = |2x + 1| − 3 |x + 2| + |x² + x − 2|, x ∈ R is not differentiable, is ______.     (JEE Main 2021)

Ans. 2
f(x) = |2x + 1| −3 |x + 2| + |x² + x − 2|


Check at 1, −2 and (-1)/2
Non. differentiable at x = 1 and (-1)/2.

Q.94. 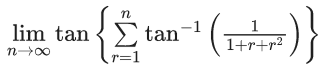 is equal to ____.    (JEE Main 2021)

Ans. 1




= tan⁻¹(2) − tan⁻¹(1) + tan⁻¹(3) − tan¹(2) + tan⁻¹(n+1) − tan⁻¹(n)
= tan⁻¹(n+1) − tan⁻¹(1)





= 1