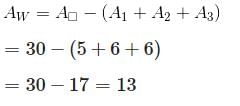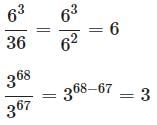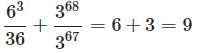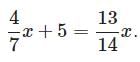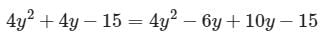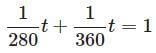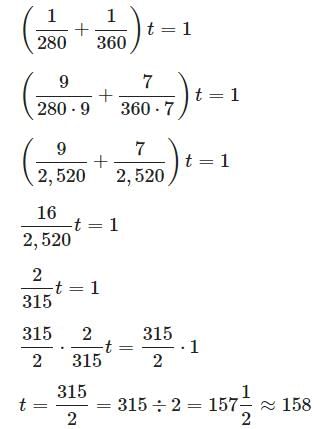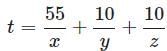Question for Quantitative Practice Questions - 4
Try yourself:How much money did Mary make this week?
Statement 1: Mary worked 40 hours of regular time and an additional 6 hours of overtime.
Statement 2: Mary made $30 an hour during normal working hours and $37 an hour during overtime.
Explanation
We need both statements to find out how much money Mary made.
Statement 1 gives the type and number of hours, and statement 2 gives the amount she made per hour. Both together are sufficient, but neither is sufficient alone.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:Solve for x:−6x − 20 = −2x + 4(1 − 3x)
Explanation
−6x − 20 = −2x + 4(1 − 3x)
−6x − 20 = −2x + 4 − 12x
−6x − 20 = −14x + 4
−6x + 14x = 4 + 20
8x = 24
x = 3
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:Solve for x.
x2 + 4x + 9 = 15
Explanation
Solve using the quadratic formula:
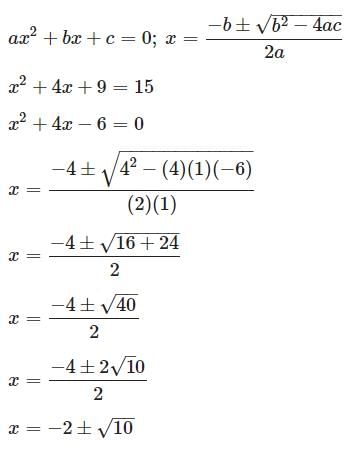
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:Rewrite as a fraction in lowest terms: 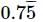
Explanation
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:A bowler had an average (arithmetic mean) score of 215 on the first 5 games she bowled. What must she bowl on the 6th game to average 220 overall?
Explanation
For the first 5 games the bowler has averaged 215. The equation to calculate the answer is

where x is the score for the sixth game. Next, to solve for the score for the 6th game (x) multiply both sides by 6:
(215⋅5) + x = 1,320
which simplifies to:
1,075 + x = 1,320
After subtracting 1,075 from each side we reach the answer:
x = 1,320 − 1,075 = 245
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:Mike, the barista at Moose Jaw Coffee, has to mix together two kinds of coffee beans - Mocha Madness, which costs $12 a pound, and Sumatra Sweetness, which costs $20 a pound - to produce forty pounds of a coffee that costs $14 a pound. The beans in the mixture sell for the same price as they would separately.
How many pounds of Mocha Madness coffee will Mike put into the mixture?
Explanation
Let M be the number of pounds of Mocha Madness coffee beans Mike uses. Then he will use (40 − M) pounds of Sumatra Sweetness coffee beans.
The Mocha Madness coffee costs $12 a pound times M pounds, or $12M dollars; similarly, the Sumatra Sweetness coffee costs $20(40 − M) . The total cost of the coffee will be 14⋅40 = $560 . Since the beans will sell for the same price as unmixed, we can add the prices to obtain and solve this equation:
12M + 20(40 − M) = 560
12M + 800 − 20M = 560
−8M + 800 = 560
−8M + 800 − 800 = 560 − 800
−8M = −240
−8M ÷ (−8) = −240 ÷ (−8)
M = 30
30 pounds of the Mocha Madness will go into the mixture.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:If the area of an equilateral is 12, given a height of 5, what is the base of the triangle?
Explanation
We derive the equation of base of a triangle from the area of a triangle formula:
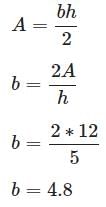
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:A cylindrical gas tank is 30 meters high and has a radius of 10 meters. How much oil can the tank hold?
Explanation
V = πr2h = π(102)30 = 3000π
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:Clara spent 1/3 of her salary on rent and 1/5 of the rest on clothes. How much did she have left after paying the rent and buying the clothes?
(1) Her salary was $3000
(2) She spent $1400 on rent and clothes
Explanation
For statement (1), she spent
1/3 x 3000 = $1000
on rent, and
15 x (3000 − 1000) = $400
on clothes.
So she spent $1000 + $400 = $1400 in total.
Therefore, she has $3000 − $1400 = $1600 left.
For statement (2), we can set Clara’s salary to be x , then we have
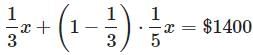
Then simplify the equation:
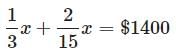
Therefore, x = $3000 .
Now we can just follow what we did for the first statement to calculate the money he had left.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:Define two sets as follows:
A = {2, 4, 6, 8, 10, a, b}
B = {1, 3, 5, 7, 9, c, d}
where a and b are distinct positive odd integers and c and d are distinct positive even integers.
How many elements are contained in the set A ∩ B ?
1) a, b ∈ {1, 3, 5, 7, 9}
2) c, d ∈ {2, 4, 6, 8, 10}
Explanation
Suppose we know a,b ∈ {1,3,5,7,9} , but we do not assume the second statement.
If c = 2 c=2 and d = 4 d=4 , then A ∩ B = {a, b, 2, 4}, a four-element set. If If c = 2 c = 2 and d = 12 d = 12 ,
Therefore, we cannot make a conclusion about the size of A∩B . A similar argument can be used to show that assuming only the second statement also does not allow a conclusion.
If we know both statements, however, A∩B = {a, b, c, d }, and we can prove that A∩B has four elements.
The answer is that both statements together are sufficient to answer this question, but neither statement alone is sufficient.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:How many hours did it take to drive from city A to city B without stopping?
1. The drive started at 10 am.
2. The average speed during the trip is 65 miles/hour.
Explanation
The total time is calculated by the equation Time = distance / rate .
Statement 2 provides the rate, but we have no information regarding distance, therefore, the quesiton is impossible to solve without more information.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:An amusement park sells Children and Adult tickets. What was the total revenue for the day?
Statement 1: The amusement park sold 259 Children tickets and 345 Adult tickets.
Statement 2: Children tickets cost $32 and Adult tickets cost $45.
Explanation
Statement 1 gives us the number of tickets sold but not the price. Insufficient.
Statement 2 gives us the price of the tickets but not the number sold. Insufficient.
Together, the two statements give us both the number of tickets sold AND the price of each ticket. From this we can calculate the total revenue.
Note: We are only trying to determine if we have enough information to answer the question. We don't have to actually do the computations!
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:A delivery truck is carrying two types of packages, green boxes and brown boxes. Green boxes weigh 10 lbs each, while brown boxes are 30 lbs each. At the weigh station, the driver notes that his load weighs exactly 400 lbs. How many green boxes does he have in his truck?
1. He is carrying exactly 20 boxes.
2. The driver never loads more brown boxes than green boxes.
Explanation
Using statement 1, we can find that he has 10 green boxes and 10 brown. We solve mixture problems using 2 equations. If we let A be the number of green boxes, and B be the number of brown boxes. We can set the equations
1) A + B = 20 and
2) 10A + 30B = 400
Solving equation 1) for A , we get A = 20 − B .
Subsituting for A into equation 2) results in
10(20 − B) + 30B = 400
Simplifying we get 200 + 20B = 400 or B = 10
Therefore, this answer would be 10 green boxes and 10 brown.
The second statement is irrelevant in finding our answer.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:Susan went to a clearance sale and bought various items on sale. She saves 20% on a purse, retailing for $100. She saves 30% on a skirt that was marked down from a retail price of $40. She also bought a jacket that was on sale, and she spent a total of $150 . How much did the jacket retail for?
1. Her overall savings were 25% off the combined retail price of all three items.
2. Her discount on the jacket was $6 more than her savings on the skirt.
Explanation
Using statement 1, it is easy to see how much the total retail amount should have been. The total retail amount discounted by 25% is the amount that Susan spent. So, we name a variable. Let x be the total retail amount. Then x - .25x = $122. We can rewrite this as x(1-.25) or x(.75) = 150 thus, x = 200. So we subtract the known retail prices of the skirt and the purse to get the retail price of the jacket. So 200 - 100 - 40 = $60 is the retail price of the jacket.
Now, we should check statement 2. Using statement 2, we can calculate the savings we had on the jacket. We can first calculate how much we saved on the skirt. So 30% of the $40 retail price is $12. After we find this, we use the information from statement 2 to find the savings we had on the jacket. So $12 + $6 = $18 saved on the jacket.
Now, we need to figure out how much we spent on the jacket. We do this by taking the total amount we spent and subtracting the discounted price of the purse and the discounted price of the skirt. So, a $100 purse, at 20% off, is $80. We calculated our savings on the skirt earlier, so we know we spent $28 on the skirt. So $150 - $80 - $28 = $42.
Now combining these two pieces of information, we see we spent $42 and saved $18 so 42+18 = $60 retail price for the jacket.
We can see that either statement alone is sufficient to solve the problem.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:A monster is holding a brown paper bag filled with cookies. Inside the bag there are two types of cookies, chocolate chip and oatmeal raisin. If the monster pulls one cookie out at random, what is the probability that he pulls out a chocolate chip cookie.
1. There are a total of 24 cookies in the bag.
2. There are 8 more chocolate chip cookies in the bag than oatmeal raisin cookies.
Explanation
We need both statements to get the answer.
Statement 1 alone is not enough. Having 24 total cookies does not tell us the proportions of each type of cookie. We could have 1 chocolate chip cookie and 23 oatmeal raisin, or vice versa.
Statement 2 alone is not sufficient either. Knowing that there are 8 more chocolate chip cookies than oatmeal raisin without knowing the total amount in the bag does not help. It could be 1 oatmeal raisin cookie and 9 chocolate chip, or it could be 100 oatmeal raisin cookies and 108 chocolate chip cookies (although that is a pretty big bag!)
Only by having both statements together can we find the right proportion. If we let A be the number of chocolate chip cookies, and B be the number of oatmeal raisin, we can set two equations and find the right ratio. We know that
A + B = 24
from statement 1, and
A = B + 8
from statement 2.
Substituting A into the first equation we get
(B + 8) + B = 24
2B = 16
B = 8
Therefore, we get 8 oatmeal raisin cookies, and 16 chocolate chip cookies. The answer is
16 / 24 = 2 / 3
or 66.67% chance that the monster pulls out a chocolate chip cookie.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:Below is a menu of the drinks served at Moonbucks Coffee:
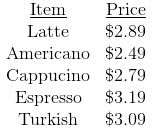
Patty and Mickey each order three beverages from the menu. Who, if either, will pay more (disregard tax)?
Statement 1: All three of Patty's drinks are Turkish coffees.
Statement 2: One of Mickey's drinks is an Americano.
Explanation
From Statement 1 alone, you know that Patty spent $3.09 × 3 = $9.27 . It is possible, however, that Mickey spent more (for three espressos, for example), just as much (on three Turkish coffees), or less (for three cappucinos, for example). Statement 2 alone gives you even more scant information, since it only tells you one beverage Mickey bought.
Suppose you know both statements. Then you know Patty spent $9.27 . You do not know how much Mickey spent, but the most he could have spent was $2.49 + 3.19 + 3.19 = $8.87 (for an Americano and two esperessos). Therefore, the two statements together are necessary and sufficient to answer the question.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:What is the perimeter of isosceles triangle ABC?
(1) AB = 32
(2) BC = 40
Explanation
(1) This statement gives us the length of one side of the triangle. This information is insufficient to solve for the perimeter.
(2) This statement gives us the length of one side of the triangle. This information is insufficient to solve for the perimeter.
Additionally, since we don't know which one of the sides ( AB or BC ) is one of the equal sides, it's impossible to determine the perimeter given the information provided.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:Which of the three sides of ΔABC has the greatest measure?
Statement 1: ∠A and ∠B are complementary angles.
Statement 2: ∠C is not an acute angle.
Explanation
The side opposite the angle of greatest measure is the longest of the three, so if we can determine which angle is the longest, we can answer this question.
It follows from Statement 1 by definition that m∠A + m∠B = 90∘ , so, since the measures of the three angles total 180∘ , m∠C = 90∘ , making ∠C right and the other two acute. This proves ∠C has the greatest measure of the three.
It follows from Statement 2 that ∠C is either right or obtuse; therefore, m∠C ≥ 90∘ .
Subsequently, the other two angles are acute, so again, ∠C has the greatest measure of the three.
From either statement alone, we can therefore identify  as the side of greatest measure.
as the side of greatest measure.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:∠A,∠B are acute. Is ∠C a right angle?
Statement 1: m∠A + m∠B < 90∘
Statement 2: c = 260
Explanation
A right triangle must have its two acute angles complementary; if Statement 1 is assumed, then this is false, the triangle is not a right triangle, and ∠C is not a right angle.
If Statement 2 is assumed, then we apply the converse of the Pythagorean Theorem to show that the triangle is not right. The sides of a triangle have the relationship
c2 = a2 + b2
only in a right triangle. If c = 260 , then the statement to be tested would be
2602 = 702 + 2402
67,600 = 4,900 + 57,600
67,600 = 62,500
This statement is false, so the triangle is not a right triangle, and ∠C is not a right angle.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:Is the triangle isosceles?
Statement 1: The triangle has vertices A(1,5), B(4,2), and C(5,6).
Statement 2: 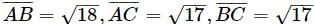
Explanation
For a triangle to be isosceles, two of the sides must be equal. To determine wheter this is true, we must have the three side lengths. Statement 2 gives us those three side lengths. However, Statement 1 also gives us all of the information we need by giving us the three vertices. By using the distance formula, we can easily get the three triangle sides from the vertices. Therefore both statements alone are sufficient.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:Two sides of a triangle are 6 and 6. What is the height of the triangle?
(1) The third side of the triangle is also 6.
(2) One of the angles of the triangle is 60∘.
Explanation
Statement (1) informs us that the triangle is an equilateral triangle, with all sides equal to 6. Therefore, the height would divide the triangle into two 30-60-90 triangles, which have side lengths in a ratio of 1: √3 :2 . For this triangle the hypotenuse would be 6 and the base would be 3. The height would therefore be 3√3 . SUFFICIENT
Statement (2) also lets you deduce that the triangle is an equilateral triangle. Since the triangle is either isoscles or equilateral (at least 2 sides are equal), that means that two angles are equal. Therefore, if one angle is 60∘ , the other two also must be 60∘ . See above. SUFFICIENT
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:Give the area of a triangle on the coordinate plane with vertices (0, 0), (2, 6), (5, 2) .
Explanation
This can be illustrated by showing this triangle inscribed inside a rectangle whose vertices are (0, 0), (5, 0), (0, 6), (5, 6) :
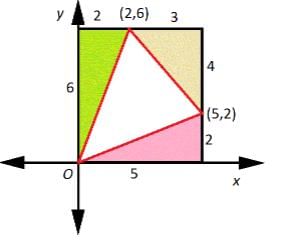
The area of the white triangle AW is the one whose area we calculate. To do this, we need the area of the square:
A = 5 x 6 = 30
The area of the red triangle:
A1 = 1/2 x 5 x 2 = 5
The area of the green triangle:
A2 = 1/2 x 6 x 2 = 6
And the area of the beige triangle:
A3 = 1/2 x 4 x 3 = 6
The area of the white triangle will be as follows: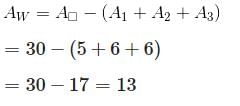
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:True or false:
ΔABC ∼ ΔDEF
Statement 1: AB / DE = BC / EF
Statement 2: ∠A ≅ ∠D and ∠B ≅ ∠E
Explanation
Statement 1 alone gives a proportion between two pairs of corresponding sides of the triangles. This is not enough to prove the triangles similar without the third side proportionality (SSS Simiilarity statement) or the congruence of the included angles (SAS Similarity statement).
Statement 2 gives two congruencies between corresponding angles, which by the Angle-Angle statement is enough to prove the triangles similar.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:A triangle contains a 110∘ angle. What are the other angles in the triangle?
(1) The triangle is isosceles.
(2)The triangle has a perimeter of 12.
Explanation
Statement 1: An isosceles triangle has two equal angles. Since the interior angles of a triangle always sum to 180∘, the only possible angles the other sides could have are 35∘ .
Statement 2: This does not provide any information relevant to the question.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:Solve |2x − 5| ≥ 3.
Explanation
It's actually easier to solve for the complement first. Let's solve \left | 2x-5 \right |<3 |2x−5|<3 . That gives -3 < 2x - 5 < 3. Add 5 to get 2 < 2x < 8, and divide by 2 to get 1 < x < 4. To find the real solution then, we take the opposites of the two inequality signs. Then our answer becomes x ≤ 1 or x ≥ 4.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:A tractor spends 5 days plowing x number of fields. How many days will it take to plow y number of fields at the same rate?
Explanation
The equation that will be used is (rate * number of days = number of fields plowed). From the first part of the question, number of fields plowed \dpi{100} \small (x) is calculated as:
rate⋅5 = x
To solve for rate both sides are divided by 5.
rate = x / 5
This rate is used for the second part of the problem. x / 5 x days = y . To solve for days, both sides are divided by x / 5 , which is the same as multiplying by 5 / x , cancelling out the x / 5 and giving the answer of days = 5y / x .
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:
Explanation
Putting these together,
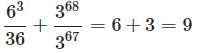
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:There is water tank already 4 / 7 full. If Jose adds 5 gallons of water to the water tank, the tank will be 13 / 14 full. How many gallons of water would the water tank hold if it were full?
Explanation
In this case, we need to solve for the volume of the water tank, so we set the full volume of the water tank as x . According to the question, 4/7 -full can be replaced as 4/7x . 13/14 -full would be 13/14x . Therefore, we can write out the equation as:
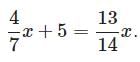
Then we can solve the equation and find the answer is 14 gallons.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:How many integers (x) can complete this inequality?
7 < 2x − 3 < 15
Explanation
7 < 2x − 3 < 15
3 is added to each side to isolate the x term:
10 < 2x < 18
Then each side is divided by 2 to find the range of x
5 < x < 9
The only integers that are between 5 and 9 are 6, 7, and 8.
The answer is 3 integers.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:Solve for z:
5z + 9 = 10
Explanation
5z + 9 = 10
5z = 10 − 9
5z = 1
z = 1 / 5
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:Factor 4y2 + 4y − 15.
Explanation
To factor this, we need two numbers that multiply to 4 x -15 = 60 and sum to 4. The numbers -6 and 10 work.
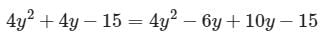
2y(2y − 3) + 5(2y − 3)
= (2y − 3)(2y + 5)
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:Steve can paint his greenhouse in 4 hours 40 minutes minutes, working alone; his brother Phil can do the same job in 6 hours, working alone. If they work together, to the nearest minute, how long will it take them?
Explanation
Think of this in terms of "greenhouses per minute", not "minutes per greenhouse". Converting hours and minutes to just minutes, Steve can paint 1 / 280 greenhouses per minute; Phil can paint 1 / 360 greenhouses per minute.
If we let t be the time in minutes that it takes to paint the greenhouse, then Steve and Phil paint 1/ 280t and 1 / 360t greenhouses, respectively; since one greenhouse total is painted, then we can add the labor and set up this equation:
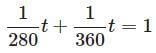
Simplify and solve:
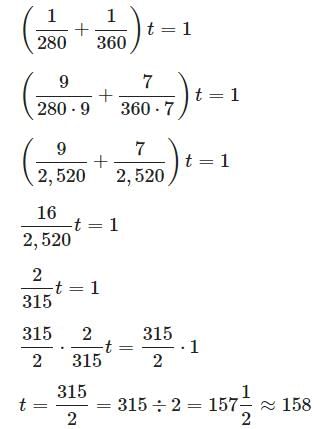
or 2 hours, 38 minutes.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:A = {2, 4, 6, 8, 10, 12,...}
B = {3, 6, 9, 12, 15, 18...}
True or false: n ∈ A ∪ B
Statement 1: n is a perfect square.
Statement 2: n is a multiple of 99.
Explanation
A includes all multiples of 2; B includes all multiples of 3. A∪B comprises all multiples of either 2 or 3.
Knowing n is a perfect square is neither necessary nor helpful, as, for example, 9 ∈ B ⊆ A ∪ B, but 25 ∉ A ∪ B (as 25 is neither a multiple of 2 nor a multiple of 3).
If you know that n is a multiple of 99, then it must also be a multiple of any number that divides 99 evenly, one such number is 3. This means n ∈ B ⊆ A ∪ B
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:The route from Tom's house to his mother's house involves traveling for 55 miles along Interstate 10, then 20 miles along State Route 34. How long does it take for Tom to travel between the two houses, if he drives at precisely the speed limit on each highway?
Statement 1: The speed limit on Interstate 10 is 70 miles per hour for the entire stretch.
Statement 2: The speed limit on State Route 34 is 50 miles per hour for the first half of the distance Tom drives on it, and 40 miles per hour for the second half.
Explanation
The rate formula RT=D - or, actually, the equivalent equation T = D/R - will help.
Let x, y, z be the speed limits along the interstate, the first half of the state route, and the second half of the state route, respectively.
Then Tom can drive I-10 in 55/x hours; the first half of SR 34, 10/y ; the second half of SR 34,10/z .
The time t it takes, in hours, for Tom to make the entire trip is the sum of these fractions:
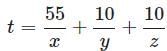
To calculate t , we need x, y, z . Statement 1 only tells us x ; Statement 2 only tells us y and z . Therefore, both together, but neither alone, are enough to allow us to calculate t .
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:Two hydrochloric acid solutions, one of concentration 40% and one of concentration 25%, are mixed together to make a solution of 35% concentration.
How much solution is made?
1) 200 ml of 40% solution is used
2) 100 ml of 25% solution is used
Explanation
Suppose we only know that 200 ml of the 40% solution is used. Then we can call x the amount of 25% solution used, and the total amount made is 200 + x . The solution equation becomes,
200(0.40) + x(0.25) = (200 + x)(0.35)
80 + 0.25x = 70 + 0.35x
10 = 0.10x
x = 10 ÷ 0.10 = 100
So 100 ml of the 25% solution is used.
Similarly, if we only know that 100 ml of the 25% solution is used, then we can call y the amount of 40% solution used, and the total amount made is 100+y . The solution equation becomes,
y(0.40) + 100(0.25) = (100 + y)(0.35)
0.40y + 25 = 35 + 0.35y
0.05y = 10
y = 10 ÷ 0.05
y = 200
So 200 ml of the 10% solution is used.
Either way, we get that
100 + 200 = 300
and 300 ml of solution is created.
The answer is that either statement is sufficient to answer the question.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:A really backward country does not use inches, feet, yards, or meters to measure distance, it uses units called wumps and zumps. These units can also be used to form units of area and volume (i.e. square wumps, cubic zumps).
How many wumps are in one zump?
Statement 1: There are 361 square wumps in one square zump.
Statement 2: There are 6,859 cubic wumps in one cubic zump.
Explanation
If there are N wumps in a zump, then there are N2 square wump in a square zump, and N3 cubic wump in a cubic zump. Therefore, given the first statement, you can take the square root of the conversion factor to get the number of wumps in a zump; given the second, you can take the cube root of that conversion factor to the same end. In both cases you get 19.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:During a semi-annual sale, the price of a shirt is discounted. Calculate the percent discount.
1. The sale price is $23.
2. The sale price is $6 less than the original price.
Explanation
In order to calculate the percent discount, both the original price and the sale price must be known. From statement 1, we know the sale price and with the additional information from statement 2, we can calculate the original price and then overall percent discount.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:Below is a menu of the drinks served at Moonbucks Coffee:
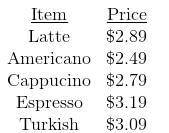
Today and today only, there is a special - buy two espressos and get any third drink free. There are no other specials.
Ralph and Janet are each ordering three beverages from this menu. Who, if either, will pay more?
Statement 1: Two of Ralph's drinks are espressos.
Statement 2: Two of Janet's drinks are cappucinos.
Explanation
Each statement alone gives information about only one order, so at the very least, both statements will be necessary.
From Statement 1, it is known that Ralph will pay $3.19 × 2 = $6.38 for his drinks, since he will only pay for the two espressos.
From Statement 2, it cannot be determined exactly what Janet will pay. However, she will pay for all three drinks, two of which are cappucinos; the least she will spend is the price of two cappucinos and an Americano, which is $2.79 + 2.79 + 2.49 = $8.07 .
From both statements together, it is definite that Janet will pay more.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:The lengths of two sides of a triangle are 6 and 8. What is the length of the third side?1. The length of the longest side is 8.
2. The triangle contains a right angle.
Explanation
Knowing that the triangle has a right angle indicates the question can be solved using the Pythagorean Theorem, however it is unclear which side is the hypotenuse. For example, if 8 is not the hypotenuse, the length of the third side is 10. If 8 is the hypotenuse, the length of the third side is 5.3.
Additionally, if you only know that 8 is the longest side, the length of the third side could be anything greater than 2 and less than 8. Therefore, having both pieces of data will allow you to solve the problem.
Report a problem
Question for Quantitative Practice Questions - 4
Try yourself:Which interior angle of ΔABC has the greatest measure?
Statement 1: (AB)2 + (BC)2 = (AC)2
Statement 2: ∠B is a right angle.
Explanation
If Statement 1 is assumed, then by the converse of the Pythagorean Theorem, the triangle is a right triangle with right angle ∠B , which is explicitly stated in Statement 2. If ∠B is a right angle, then the other two angles are acute, since a triangle must have at least two acute angles. A right angle measures 90∘ and an acute angle measures less, so from either statement, we can deduce that ∠B is the angle with greatest measure.
Report a problem

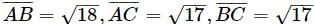
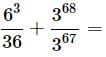


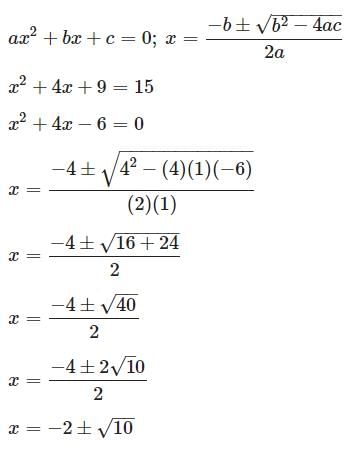
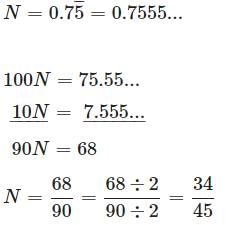

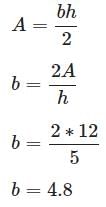
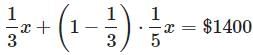
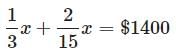
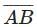 as the side of greatest measure.
as the side of greatest measure.